正则化实战( Lasso 套索回归,Ridge 岭回归)

本文主要是介绍正则化实战( Lasso 套索回归,Ridge 岭回归)，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

Lasso 套索回归

导入包

import numpy as np
from sklearn.linear_model import Lasso
from sklearn.linear_model import SGDRegressor, LinearRegression

原方程的计算结果

# 1. 创建数据集X，y
X = 2 * np.random.rand(100, 20)
w = np.random.rand(20, 1)
b = np.random.randint(1, 10, size=1)
y = X.dot(w) +b + np.random.randn(100,1)
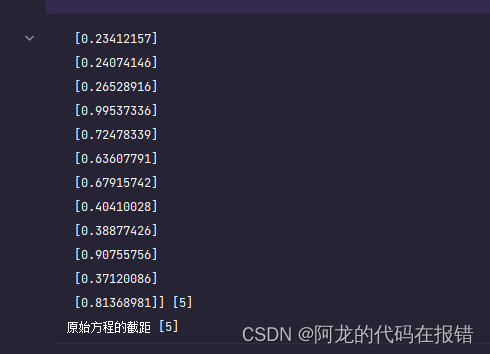
print('原始方程的斜率：',w,b)
print('原始方程的截距',b)

在这里插入图片描述

普通线性回归方式

# 线性回贵
linear = LinearRegression()
linear.fit(X,y)
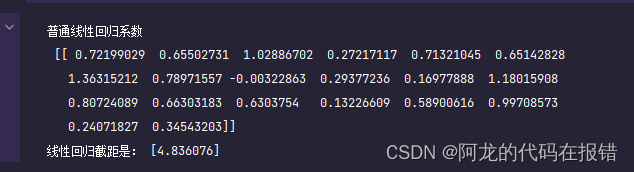
print('普通线性回归系数\n',linear.coef_)
print('线性回归截距是：',linear.intercept_)

在这里插入图片描述

Lasso 套索回归

# l1 正则化的lasso回归一部分权重变为0
# 其余的进行了衰减     可以说模型的负责度降低，可以减少过拟合
lasso = Lasso(alpha=0.1)
lasso.fit(X,y)
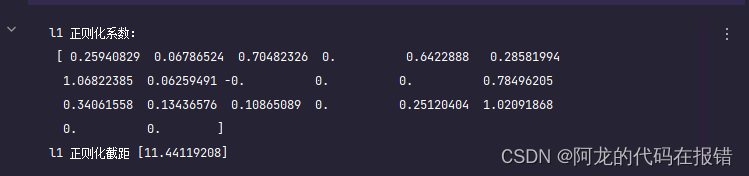
print('l1 正则化系数：\n',lasso.coef_)
print('l1 正则化截距',lasso.intercept_)

在这里插入图片描述

随机的梯度下降

sgd = SGDRegressor(penalty='l1',alpha=0.1)
sgd.fit(X,y.ravel())
print('随机梯度下降系数',sgd.coef_)
print('随机梯度截距',sgd.intercept_)

在这里插入图片描述

和没有正则项约束线性回归对比，可知L1正则化，将方程系数进行了缩减，部分系数为0，产生稀疏模型
$\alpha$ 越大，模型稀疏性越强，越多的参数为0
Lasso回归源码解析：
alpha：正则项系数
fit_intercept：是否计算 $w_0$ 截距项
normalize：是否做归一化
precompute：bool 类型，默认值为False，决定是否提前计算Gram矩阵来加速计算
max_iter：最大迭代次数
tol：结果的精确度
warm_start：bool类型，默认值为False。如果为True，那么使⽤用前⼀次训练结果继续训练。否则从头开始训练

Ridge 岭回归

导入包

import numpy as np
from sklearn.linear_model import Ridge
from sklearn.linear_model import SGDRegressor
from sklearn.linear_model import LinearRegression

原方程的计算结果


# 创建模拟数据
X = 2 * np.random.rand(100,5)
w = np.random.randint(1,10,size=(5,1))
b = np.random.randint(1,10,size=1)
y = X.dot(w) + b + np.random.randn(100,1)print('原始方程的斜率:',w.ravel())
print('原始方程的截距',b)

在这里插入图片描述

普通的线性回归

linear = LinearRegression()
linear.fit(X,y)
print('普通的线性回归系数',linear.coef_,linear.intercept_)**

在这里插入图片描述

Ridge 岭回归

ridge = Ridge(alpha=0.12)
ridge.fit(X,y)
print('l2 正则化ridge系数数：',ridge.coef_,ridge.intercept_)

在这里插入图片描述

结论：

和没有正则项约束线性回归对比，可知L2正则化，将方程系数进行了缩小
$\alpha$ 增大求解出来的方程斜率变小
Ridge回归源码解析：
alpha：正则项系数
fit_intercept：是否计算 $w_0$ 截距项
normalize：是否做归一化
max_iter：最大迭代次数
tol：结果的精确度
solver：优化算法的选择