本文主要是介绍一维Burgers方程数值解法,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
一维Burgers方程
一维burgers方程为:
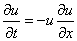
由于等式右边可以进行积分:
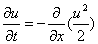
利用F = u**2,则方程为:
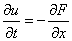
假设u初始为阶跃函数:
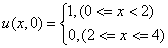
数值解法采用MacCormack格式:
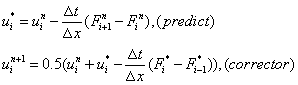
但是这一解法,有失真的性质,后面具体介绍。
所以根据这一格式,可以直接数值求解,并利用matplotlib画出动态的数值图形,具体代码如下:
# -*- coding: utf-8 -*-
"""
Created on Tue Jan 20 14:32:23 2015
1D burges equation
@author: myjiayan
"""import numpy as np
import matplotlib.pyplot as plt
from matplotlib import animationdef u_initial():first = np.ones(40)second = np.zeros(41)result = np.array(list(first)+list(second))return resultdef computeF(u):F = 0.5*u**2return Fdef maccormack(u,nt,dt,dx):un = np.zeros((nt,len(u)))un[0] = u.copy()ustar = u.copy()for t in xrange(1,nt):F = computeF(u)ustar[:-1] = u[:-1] - (F[1:]-F[:-1])*dt/dxustar[-1] = 0.0Fstar = computeF(ustar)un[t,1:] = 0.5*(u[1:]+ustar[1:]-(Fstar[1:]-Fstar[:-1])*dt/dx)un[t,0] = 1.0u = un[t].copy()return unif __name__ == '__main__':nx = 81nt = 70dx = 4.0/(nx-1)def animate(data):x = np.linspace(0,4,nx)y = dataline.set_data(x,y)return line,u = u_initial()sigma = .5dt = sigma*dxun = maccormack(u,nt,dt,dx)fig = plt.figure();ax = plt.axes(xlim=(0,4),ylim=(-.5,2));line, = ax.plot([],[],lw=2);anim = animation.FuncAnimation(fig, animate, frames=un, interval=50)plt.show() 直接将代码保存为burgers.py文件,打开terminal:
$python burgers.py
数值结果就以动态的形式表现出来了。
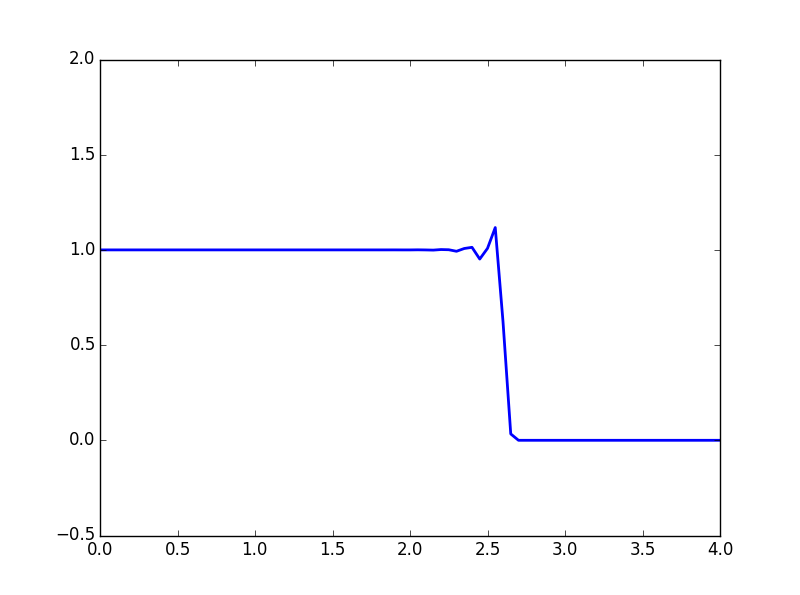
很明显,数值结果失真了,数值结果中u的值竟然比1大,如何改进MacCormack格式呢?
我们在预测步上加一个人工项,新的格式为:
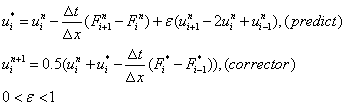
选取Ephsilon为0.5后改进格式得到的数值结果为:
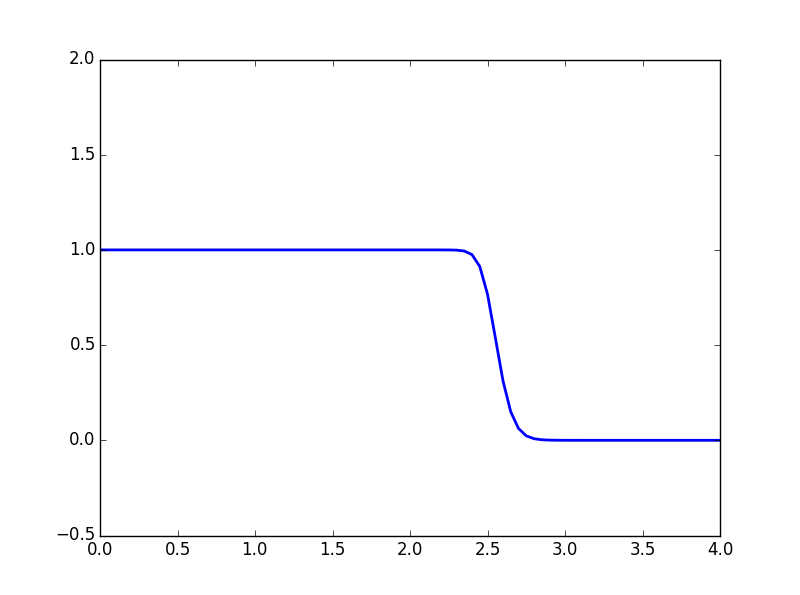
比1大的值已经消失。
这篇关于一维Burgers方程数值解法的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!









