莫凡pyTorch1

2023-12-11 20:10
文章标签 莫凡 pytorch1

本文主要是介绍莫凡pyTorch1，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

文章目录

  • 一、torch与numpy
    • 1.绝对值、三角函数、平均值
    • 2.矩阵乘法
    • 3.画出四个激活函数
  • 二、回归分类
    • 1.画回归散点图
    • 2.回归网络
    • 3.分类网络
    • 4.两种搭建框架（画图纸）的方法
    • 5. 保存网络和提取网络
    • 6.批训练 minibatch trainning
    • 7.优化器Optimizer
  • 总结

一、torch与numpy

1.绝对值、三角函数、平均值

import torch
import numpy as npnp_data = np.arange(6).reshape((2, 3))
# numpy转torch
torch_data = torch.from_numpy(np_data)
# torch转numpy
tensor2array = torch_data.numpy()

调用绝对值、三角函数、平均值等，numpy与torch基本一样

data = [-1, -2, 1, 2]
# torch.FloatTensor将list ,numpy转化为tensor（32位浮点）
tensor = torch.FloatTensor(data)  # 32-bit floating pointnp.abs(data)
torch.abs(tensor)np.sin(data)
torch.sin(tensor)

2.矩阵乘法

# matrix multiplication
data = [[1,2], [3,4]]
tensor = torch.FloatTensor(data)  # 32-bit floating pointnp.matmul(data, data),     # [[7, 10], [15, 22]]
data.dot(data)    //np.dot可以用，tensor.dot只接受一维数组计算，tensor.dot![请添加图片描述](https://img-blog.csdnimg.cn/0f8afe74a8134d4d845f64831f79ac0b.png)
改用mm
torch.mm(tensor, tensor)   # [[7, 10], [15, 22]]
tensor.mm(tensor, tensor)tensor.mm(tensor)                       //矩阵乘法
结果	tensor([[  7.,  10.],[ 15.,  22.]])
tensor * tensor                         //对位相乘
结果	tensor([[  1.,   4.],[  9.,  16.]])
torch.dot(torch.Tensor([2, 3]), torch.Tensor([2, 1]))      //dot一维数组相乘
结果	   tensor(7.)

1.0版本之前variable在旧版本中可以反向传播；1.0版本删掉了variable，tensor可直接反向传播；当前版本又可以用了

import torch
from torch.autograd import Variable
tensor = torch.FloatTensor([[1,2],[3,4]])            # build a tensor
variable = Variable(tensor, requires_grad=True)

也可用tensor替代variable

tensor = torch.tensor([[1,2],[3,4]], dtype=float, requires_grad=True)         # build a tensor
print(tensor)       # [torch.FloatTensor of size 2x2]运行结果：
tensor([[1., 2.],[3., 4.]], dtype=torch.float64, requires_grad=True)

tensor = torch.tensor([[1,2],[3,4]], dtype=float, requires_grad=True) # build a tensor
t_out = torch.mean(tensor*tensor)
print(t_out)
t_out.backward()     //反向传播，计算梯度
print(tensor.grad)    //打印出梯度运行结果：
tensor(7.5000, dtype=torch.float64, grad_fn=<MeanBackward0>)
tensor([[0.5000, 1.0000],[1.5000, 2.0000]], dtype=torch.float64)

梯度计算过程（求导过程）
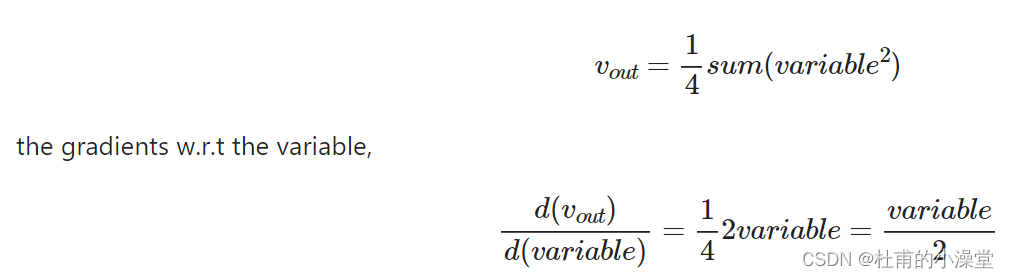
梯度计算过程
直接打印出数据，以下两个都可，结果一样

print(tensor.data.numpy())
print(tensor.detach().numpy())
运行结果：
[[1. 2.][3. 4.]]

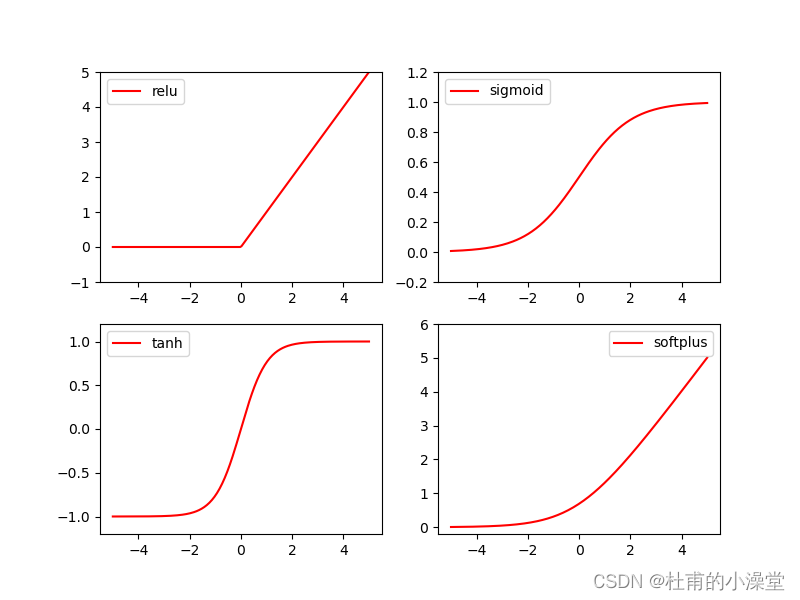
3.画出四个激活函数

import torch
import  torch.nn.functional as F
from torch.autograd import Variable
import matplotlib.pyplot as plt# torch.linspace返回一个一维的tensor（张量），包含了从start到end（包括端点）的等距的steps个数据点。
x = torch.linspace(-5,5,200)
x = Variable(x)
x_np = x.data.numpy()# matplot需要将矩阵数据变成数组，才能对应x画成直线
y_relu = F.relu(x).data.numpy()
y_sigmoid = F.sigmoid(x).data.numpy()
y_tanh = F.tanh(x).data.numpy()
# F.softmax用来做概率图
y_softplus = F.softplus(x).data.numpy()

在这里插入图片描述

二、回归分类

1.画回归散点图

# torch.unsqueeze()给数据增加维度；torch.squeeze()对数据降维；torch.linspace(3,10,5)返回从3到10等距离的5个一维张量
x = torch.unsqueeze(torch.linspace(-1, 1, 100), dim=1)  # x data (tensor), shape=(100, 1)
# pow(2)表示x的2次方，也有math.pow(x,2)的写法；torch.rand(*sizes, out=None) 作为噪声点，保持和x一个形状，返回[0,1)之间的均匀分布
y = x.pow(2) + 0.2*torch.rand(x.size())     # noisy y data (tensor), shape=(100, 1)x, y = Variable(x),Variable(y)
# scatter打印散点图
plt.scatter(x.data.numpy(), y.data.numpy())
plt.show()

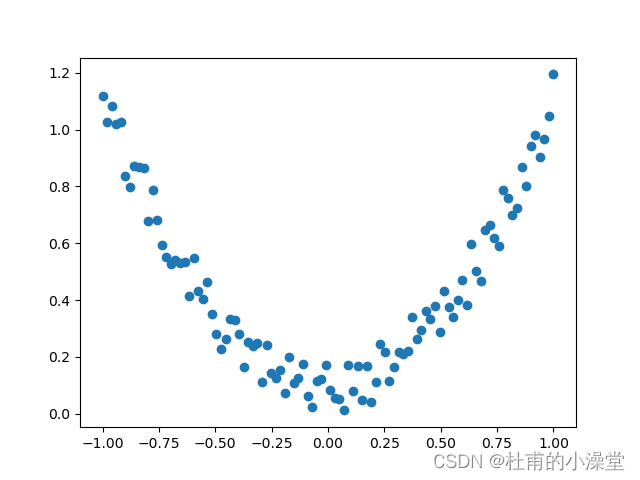
在这里插入图片描述

2.回归网络

class Net(torch.nn.Module):  # 本类继承torch的Module模块，来作为net的主模块def __init__(self, n_feature, n_hidden, n_output):  # 搭建层的信息，相当于画图纸super(Net, self).__init__()  # super为官方定义的格式# nn.Linear对输入数据做线性变换y=wx+b，并学习更新偏置b的值；Linear需要输入两个参数（上一层神经元的个数，本层的神经元个数）self.hidden = torch.nn.Linear(n_feature, n_hidden)  # hidden layerself.predict = torch.nn.Linear(n_hidden, n_output)  # output layerdef forward(self, x):  # 前向传递，相当于根据图纸盖楼x = F.relu(self.hidden(x))  # 隐含层用激活函数激活x = self.predict(x)  # x放入输出层输出，输出一般不用激活函数，会影响结果return xnet = Net(1, 10, 1)
print(net)运行结果：
Net((hidden): Linear(in_features=1, out_features=10, bias=True)(predict): Linear(in_features=10, out_features=1, bias=True)
)

# 构建一个optimizer对象，用来保持当前参数状态并基于计算得到的梯度进行参数更新
optimizer = torch.optim.SGD(net.parameters(), lr=0.2)   # 使用SGD随机梯度下降法优化，学习步长一般小于1
# 对SGD说明：普通训练方法，重复不断的把整套数据放入神经网络NN中训练，消耗的计算资源会很大；
# SGD会把数据拆分后再分批不断放入NN中计算，虽然不能反映整体数据的情况,不过却很大程度上加速NN的训练过程,而且也不会丢失太多准确率.
loss_func = torch.nn.MSELoss()  # 均方差作为损失函数plt.ion()   # matplot实时打印for t in range(100):# x是之前定义的100个数，net(x)是100个数经过神经网络（正向传播）后的100个值prediction = net(x)  # 预测；input x and predict based on x# 训练4步loss = loss_func(prediction, y)  # 计算损失；输入格式固定(1. nn output, 2. target)optimizer.zero_grad()  # 梯度清零；即求导前将导数归0，为了能使误差函数取到极小值（局部最优）loss.backward()  # 计算当前梯度，反向传播，来实现可训练参数的更新optimizer.step()  # 在backward()之类的函数计算好后调用这个函数，更新所有的参数if t % 10 == 0:    # 每学习5步打印一次# plot and show learning processplt.cla()plt.scatter(x.data.numpy(), y.data.numpy())plt.plot(x.data.numpy(), prediction.data.numpy(), 'r-', lw=5)plt.text(0.5, 0, 'Loss=%.4f' % loss.data.numpy(), fontdict={'size': 20, 'color': 'red'})plt.show()plt.pause(0.1)plt.ioff()

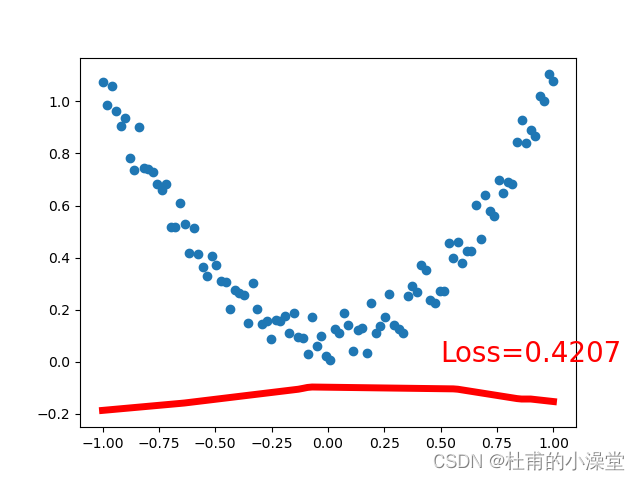
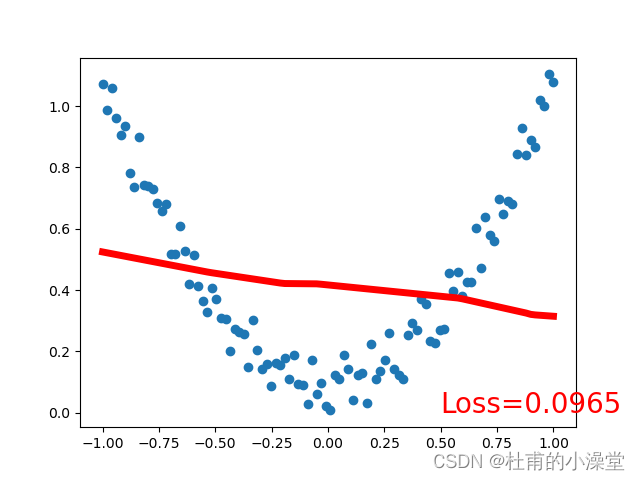
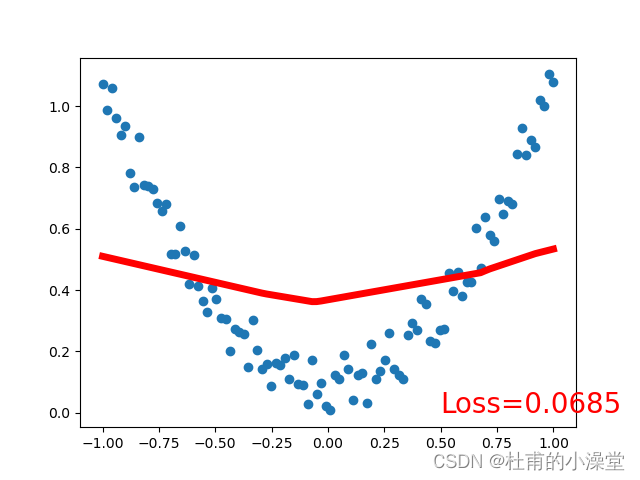
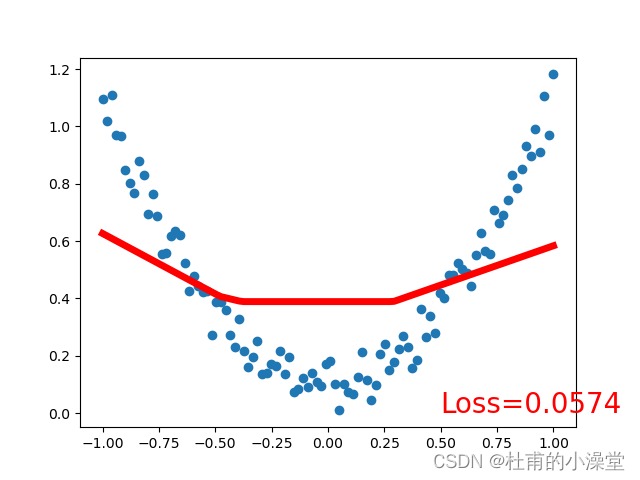
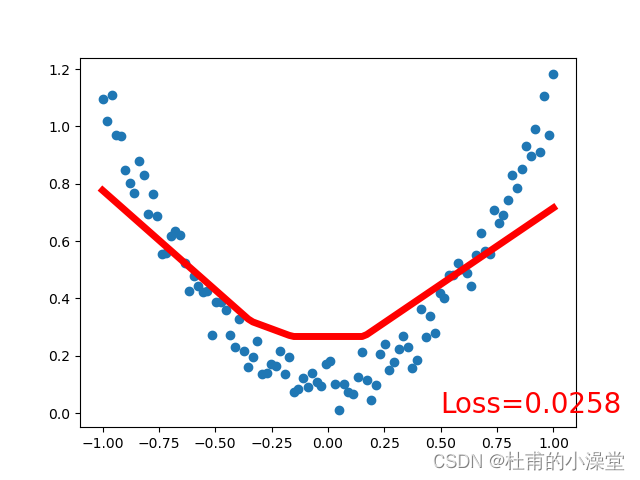
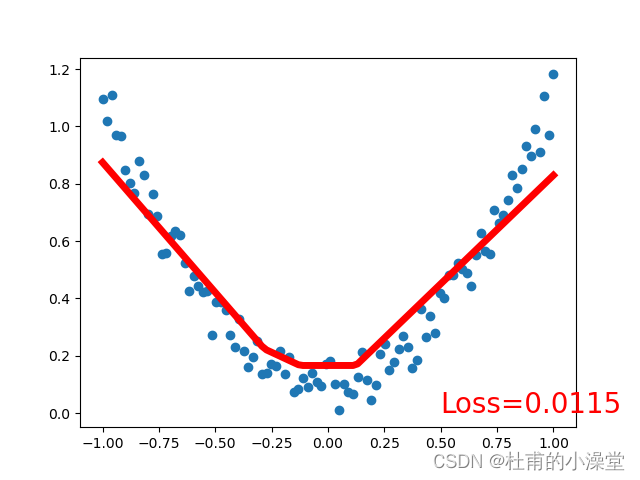
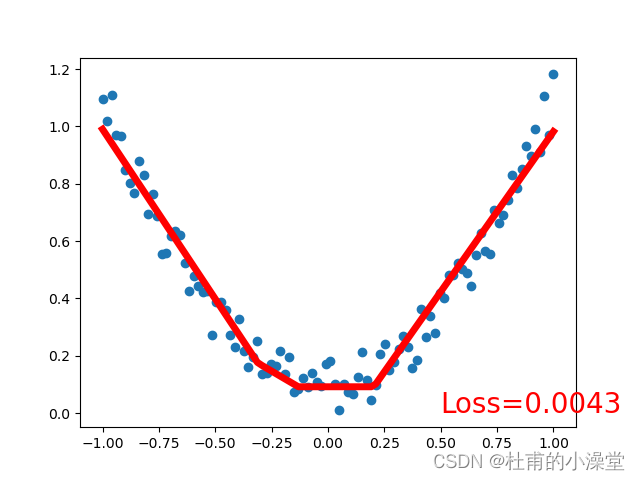
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

在这里插入图片描述

3.分类网络

import torch
from torch.autograd import Variable
import torch.nn.functional as F  # 包含了构筑神经网络结构基本元素的包
import matplotlib.pyplot as plt# 假设数据
n_data = torch.ones(100, 2)  # 生成100行2列的张量
x0 = torch.normal(2 * n_data, 1)  # 随机生成均值为2 * n_data，标准差为1的正态分布，shape=(100, 2)
y0 = torch.zeros(100)  # y-shape=(100, 1)
x1 = torch.normal(-2 * n_data, 1)  # 随机生成均值为-2 * n_data，标准差为1的正态分布，shape=(100, 2)
y1 = torch.ones(100)  # class1 y data (tensor), shape=(100, 1)
# torch.cat将两个张量（tensor）拼接在一起，0为上下拼接，1为左右拼接
x = torch.cat((x0, x1), 0).type(torch.FloatTensor)  # shape (200, 2) FloatTensor = 32-bit floating
y = torch.cat((y0, y1), ).type(torch.LongTensor)  # shape (200,) LongTensor = 64-bit integer# 神经网络只能输入variable形式，要把变装入variable容器里
x, y = Variable(x), Variable(y)plt.scatter(x.data.numpy()[:, 0], x.data.numpy()[:, 1], c=y.data.numpy(), s=100, lw=0, cmap='RdYlGn')
plt.show()class Net(torch.nn.Module):  # 本类继承torch的Module模块，来作为net的主模块def __init__(self, n_feature, n_hidden, n_output):  # 搭建层的信息，相当于画图纸super(Net, self).__init__()  # super为官方定义的格式# nn.Linear对输入数据做线性变换y=wx+b，并学习更新偏置b的值；Linear需要输入两个参数（上一层神经元的个数，本层的神经元个数）self.hidden = torch.nn.Linear(n_feature, n_hidden)  # hidden layerself.predict = torch.nn.Linear(n_hidden, n_output)  # output layerdef forward(self, x):  # 前向传递，相当于根据图纸盖楼x = F.relu(self.hidden(x))  # 隐含层用激活函数激活x = self.predict(x)  # x放入输出层输出，输出一般不用激活函数，会影响结果return x# 分类任务常用到One-Hot向量：一个向量中只有某一项为1，其余全为0
net = Net(n_feature=2, n_hidden=10, n_output=2)  # 有两个输入例子，分类成2类
print(net)  # net architecture# 构建一个optimizer对象，用来保持当前参数状态并基于计算得到的梯度进行参数更新
optimizer = torch.optim.SGD(net.parameters(), lr=0.02)  # 使用SGD随机梯度下降法优化，学习步长一般小于1
# 对SGD说明：普通训练方法，重复不断的把整套数据放入神经网络NN中训练，消耗的计算资源会很大；
# SGD会把数据拆分后再分批不断放入NN中计算，虽然不能反映整体数据的情况,不过却很大程度上加速NN的训练过程,而且也不会丢失太多准确率.
loss_func = torch.nn.CrossEntropyLoss()  # 通过交叉熵损失函数将One-Hot转化成总和为1的概率,如[0.1, 0.2, 0.7]plt.ion()  # matplot实时打印for t in range(100):# x是之前定义的100个数，net(x)是100个数经过神经网络（正向传播）后的100个值out = net(x)  # 预测；input x and predict based on x# prediction = torch.max(F.softmax(out, dim=1), 1)[1]  由于CrossEntropy包含了softmax激活函数，所以这里不再加# 训练4步loss = loss_func(out, y)  # 计算损失；输入格式固定(1. nn output, 2. target)optimizer.zero_grad()  # 梯度清零；即求导前将导数归0，为了能使误差函数取到极小值（局部最优）loss.backward()  # 计算当前梯度，反向传播，来实现可训练参数的更新optimizer.step()  # 在backward()之类的函数计算好后调用这个函数，更新所有的参数if t % 10 == 0 or t in [3, 6]:# plot and show learning processplt.cla()_, prediction = torch.max(F.softmax(out), 1)   # torch.max返回值有两个，第一个是max是多少，第二个是max的indexpred_y = prediction.data.numpy().squeeze()target_y = y.data.numpy()plt.scatter(x.data.numpy()[:, 0], x.data.numpy()[:, 1], c=pred_y, s=100, lw=0, cmap='RdYlGn')accuracy = sum(pred_y == target_y) / 200.plt.text(1.5, -4, 'Accuracy=%.2f' % accuracy, fontdict={'size': 20, 'color': 'red'})plt.show()plt.pause(0.1)plt.ioff()

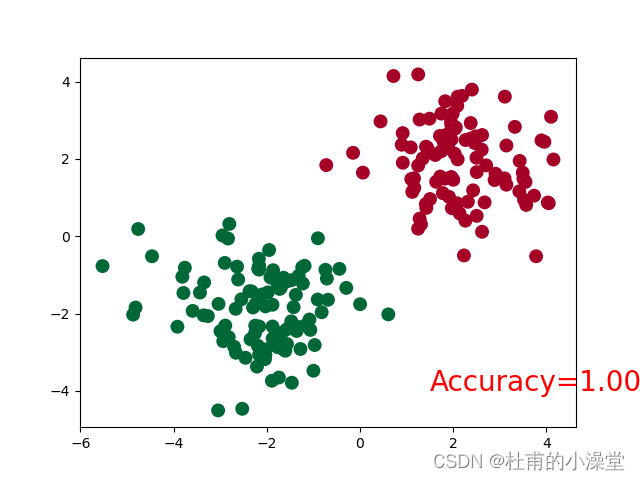
在这里插入图片描述

4.两种搭建框架（画图纸）的方法

//method1         建立net类,并实例化
class Net(torch.nn.Module):  # 本类继承torch的Module模块，来作为net的主模块def __init__(self, n_feature, n_hidden, n_output):  # 搭建层的信息，相当于画图纸super(Net, self).__init__()  # super为官方定义的格式# nn.Linear对输入数据做线性变换y=wx+b，并学习更新偏置b的值；Linear需要输入两个参数（上一层神经元的个数，本层的神经元个数）self.hidden = torch.nn.Linear(n_feature, n_hidden)  # hidden layerself.predict = torch.nn.Linear(n_hidden, n_output)  # output layerdef forward(self, x):  # 前向传递，相当于根据图纸盖楼x = F.relu(self.hidden(x))  # 隐含层用激活函数激活x = self.predict(x)  # x放入输出层输出，输出一般不用激活函数，会影响结果return x
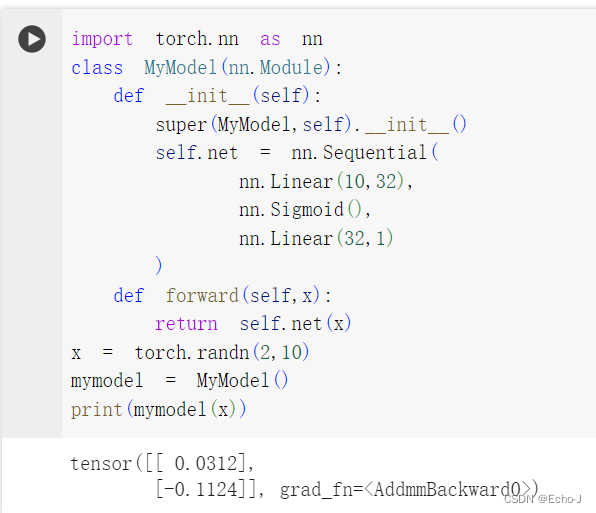
net1 = Net(1, 10, 1)//method2     调用Sequential来实例化
# easy and fast way to build your network
net2 = torch.nn.Sequential(torch.nn.Linear(1, 10),torch.nn.ReLU(),torch.nn.Linear(10, 1)
)

print(net1)     # net1 architecture
print(net2)运行结果：Net ((hidden): Linear (1 -> 10)(predict): Linear (10 -> 1)
)
Sequential ((0): Linear (1 -> 10)(1): ReLU ()(2): Linear (10 -> 1)
)

5. 保存网络和提取网络

（用于保存训练了一半的网络，提取处理继续训练）

import torch
from torch.autograd import Variable
import matplotlib.pyplot as plttorch.manual_seed(1)x = torch.unsqueeze(torch.linspace(-1, 1, 100), dim=1)  # x data (tensor), shape=(100, 1)
y = x.pow(2) + 0.2*torch.rand(x.size())  # noisy y data (tensor), shape=(100, 1)
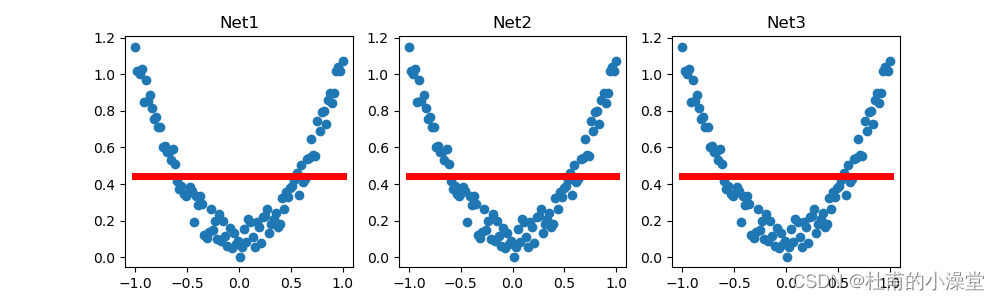
x, y = Variable(x, requires_grad=False), Variable(y, requires_grad=False)def save():# 快速搭建法net1 = torch.nn.Sequential(torch.nn.Linear(1, 10),     # 隐藏层torch.nn.ReLU(),            # 隐藏层的激活函数torch.nn.Linear(10, 1)      # 输出层)optimizer = torch.optim.SGD(net1.parameters(), lr=0.5)loss_func = torch.nn.MSELoss()for t in range(100):prediction = net1(x)loss = loss_func(prediction, y)optimizer.zero_grad()loss.backward()optimizer.step()# plot resultplt.figure(1, figsize=(10, 3))plt.subplot(131)plt.title('Net1')plt.scatter(x.data.numpy(), y.data.numpy())plt.plot(x.data.numpy(), prediction.data.numpy(), 'r-', lw=5)# 2 ways to save the nettorch.save(net1, 'net.pkl')  # 保留整个网络，以.pkl格式保持torch.save(net1.state_dict(), 'net_params.pkl')   # 保留节点参数# 提取保存的网络
def restore_net():# restore entire net1 to net2net2 = torch.load('net.pkl')   # 以.load函数提取保存的网络prediction = net2(x)           # 这里将x导入net传给prediction是为了画图# plot resultplt.subplot(132)plt.title('Net2')plt.scatter(x.data.numpy(), y.data.numpy())plt.plot(x.data.numpy(), prediction.data.numpy(), 'r-', lw=5)# 提取保存网络的参数
def restore_params():# restore only the parameters in net1 to net3# 提取保存的保留参数需先自己快速建一个网络，提取网络参数比提取整个网络速度快，推荐使用net3 = torch.nn.Sequential(torch.nn.Linear(1, 10),torch.nn.ReLU(),torch.nn.Linear(10, 1))# copy net1's parameters into net3net3.load_state_dict(torch.load('net_params.pkl'))      # 使用.load_state_dict函数进行prediction = net3(x)        # 画图传参# plot resultplt.subplot(133)plt.title('Net3')plt.scatter(x.data.numpy(), y.data.numpy())plt.plot(x.data.numpy(), prediction.data.numpy(), 'r-', lw=5)plt.show()save()
# restore entire net (may slow)
restore_net()
# restore only the net parameters
restore_params()

在这里插入图片描述

6.批训练 minibatch trainning

数据过大时，将数据分成多批次进行训练，来提升训练速度和训练效率

import torch
import torch.utils.data as Data   # 使用data模块来进行小批训练# 每小批抽取5个数据训练
BATCH_SIZE = 5# linspace返回一个一维的tensor（张量），包含了从start=1到end=10（包括端点）的等距的steps=10个数据点。
x = torch.linspace(1, 10, 10)       # this is x data (torch tensor)
y = torch.linspace(10, 1, 10)# 将数据放入torch的数据库TensorDataset中
torch_dataset = Data.TensorDataset(x, y)  # 训练数据data_tensor，计算误差数据target_tensor
loader = Data.DataLoader(       # loader\DataLoader将数据变成小批dataset=torch_dataset,      # torch TensorDataset formatbatch_size=BATCH_SIZE,      # mini batch sizeshuffle=True,               # 是否先将数据打乱，再进行抽样；false为不打乱num_workers=0,              # 加载数据进程数；用cpu和windows跑需要设置=0；GPU跑多设几个，加快寻批速度
)for epoch in range(3):   # 把所以数据整体训练3次# enumerate给loader中每个数据加一个索引for step, (batch_x, batch_y) in enumerate(loader):  # for each training step# train your data...print('Epoch: ', epoch, '| Step: ', step, '| batch x: ',batch_x.numpy(), '| batch y: ', batch_y.numpy())运行结果：
Epoch:  0 | Step:  0 | batch x:  [6. 8. 2. 7. 5.] | batch y:  [5. 3. 9. 4. 6.]
Epoch:  0 | Step:  1 | batch x:  [ 1. 10.  4.  3.  9.] | batch y:  [10.  1.  7.  8.  2.]
Epoch:  1 | Step:  0 | batch x:  [4. 6. 1. 7. 8.] | batch y:  [ 7.  5. 10.  4.  3.]
Epoch:  1 | Step:  1 | batch x:  [10.  5.  9.  2.  3.] | batch y:  [1. 6. 2. 9. 8.]
Epoch:  2 | Step:  0 | batch x:  [5. 9. 8. 7. 6.] | batch y:  [6. 2. 3. 4. 5.]
Epoch:  2 | Step:  1 | batch x:  [ 2. 10.  3.  1.  4.] | batch y:  [ 9.  1.  8. 10.  7.]

7.优化器Optimizer

import torch
import torch.utils.data as Data
import torch.nn.functional as F
from torch.autograd import Variable
import matplotlib.pyplot as plt# 定义超参数（全大写，提前赋值定义） hyper parameters
LR = 0.01
BATCH_SIZE = 32
EPOCH = 12# fake dataset
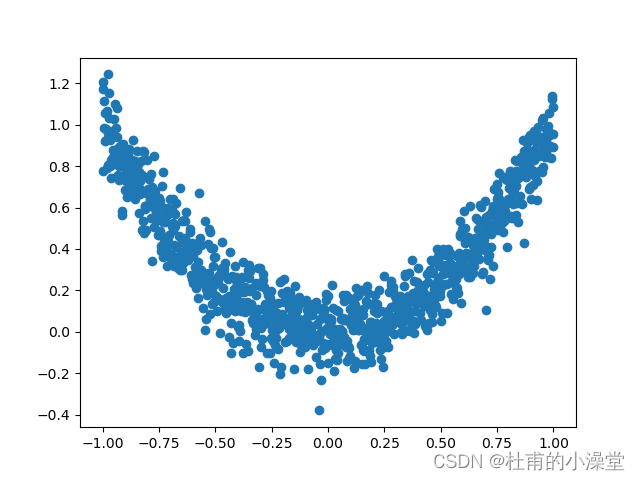
x = torch.unsqueeze(torch.linspace(-1, 1, 1000), dim=1)
y = x.pow(2) + 0.1 * torch.normal(torch.zeros(*x.size()))# plot dataset
plt.scatter(x.numpy(), y.numpy())
plt.show()# minibatch training需要写dataset和loader
torch_dataset = Data.TensorDataset(x, y)
loader = Data.DataLoader(dataset=torch_dataset,batch_size=BATCH_SIZE,shuffle=True,      # 一般用shuffle=true，打乱数据会有更好的训练效果num_workers=0, )   # windows中num_works=0，=0用主线程cpu跑class Net(torch.nn.Module):def __init__(self):super(Net, self).__init__()self.hidden = torch.nn.Linear(1, 20)  # 隐含层有20个神经元self.predict = torch.nn.Linear(20, 1)  # output layerdef forward(self, x):x = F.relu(self.hidden(x))  # activation function for hidden layerx = self.predict(x)  # linear outputreturn x# 定义4个不同的神经网络，后续使用不同的优化器进行优化
net_SGD = Net()
net_Momentum = Net()
net_RMSprop = Net()
net_Adam = Net()
nets = [net_SGD, net_Momentum, net_RMSprop, net_Adam]  # 将定义的网络放在一个list中，方便for循环提取，一个一个训练# 建立对应网络的优化器
opt_SGD = torch.optim.SGD(net_SGD.parameters(), lr=LR)
opt_Momentum = torch.optim.SGD(net_Momentum.parameters(), lr=LR, momentum=0.8)  # 动态SGD
opt_RMSprop = torch.optim.RMSprop(net_RMSprop.parameters(), lr=LR, alpha=0.9)
opt_Adam = torch.optim.Adam(net_Adam.parameters(), lr=LR, betas=(0.9, 0.99))
optimizers = [opt_SGD, opt_Momentum, opt_RMSprop, opt_Adam]    # 放一个优化器list#  创建损失函数
loss_func = torch.nn.MSELoss()
losses_his = [[], [], [], []]   # 创建误差list，记录4个损失函数的误差变化曲线# training
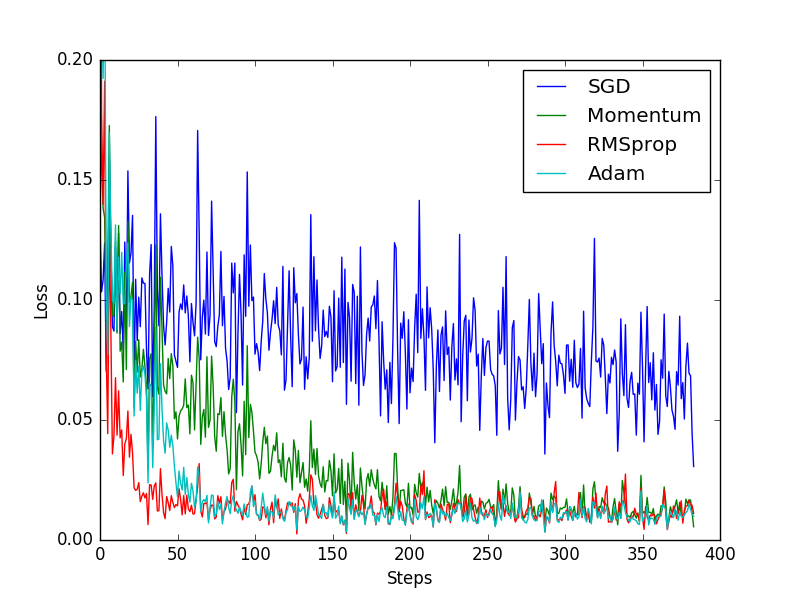
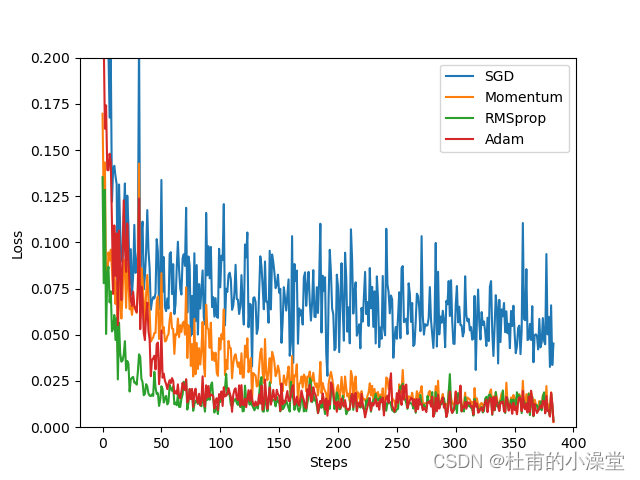
for epoch in range(EPOCH):print('Epoch: ', epoch)for step, (batch_x, batch_y) in enumerate(loader):          # for each training stepb_x = Variable(batch_x)    # 改版后用不用variable包装都可以b_y = Variable(batch_y)	   # 不包装直接赋值，b_y = batch_yfor net, opt, l_his in zip(nets, optimizers, losses_his):output = net(b_x)              # get output for every netloss = loss_func(output, b_y)  # compute loss for every netopt.zero_grad()                # clear gradients for next trainloss.backward()                # backpropagation, compute gradientsopt.step()                     # apply gradientsl_his.append(loss.item())     # loss recoderlabels = ['SGD', 'Momentum', 'RMSprop', 'Adam']
for i, l_his in enumerate(losses_his):plt.plot(l_his, label=labels[i])
plt.legend(loc='best')
plt.xlabel('Steps')
plt.ylabel('Loss')
plt.ylim((0, 0.2))
plt.show()

在这里插入图片描述
在这里插入图片描述

总结

提示：这里对文章进行总结：
例如：以上就是今天要讲的内容，本文仅仅简单介绍了pandas的使用，而pandas提供了大量能使我们快速便捷地处理数据的函数和方法。

这篇关于莫凡pyTorch1的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/481957。

相关文章

莫凡Pytorch学习笔记（六）

莫凡Pytorch学习笔记（六）

Pytorch中的mini-batch和优化器 本篇笔记主要对应于莫凡Pytorch中的3.5和3.6节。主要讲了如何使用Pytorch中的mini-batch和优化器。 Pytorch中的mini-batch 在笔记二、三中搭建的网络中，我们是一次性直接将整个训练集送进网络，这种方式称为Full Batch Learning。但是当数据量很大时，首先一次性加载这么多数据收到了内存的限制，同
阅读更多...
莫凡Pytorch学习笔记（五）

莫凡Pytorch学习笔记（五）

Pytorch模型保存与提取 本篇笔记主要对应于莫凡Pytorch中的3.4节。主要讲了如何使用Pytorch保存和提取我们的神经网络。 我们将通过两种方式展示模型的保存和提取。 第一种保存方式是保存整个模型，在重新提取时直接加载整个模型。第二种保存方法是只保存模型的参数，这种方式只保存了参数，而不会保存模型的结构等信息。 两种方式各有优缺点。保存完整模型不需要知道网络的结构，一次性保存一次
阅读更多...
机器学习-pytorch1（持续更新）

机器学习-pytorch1（持续更新）

上一节我们学习了机器学习的线性模型和非线性模型的机器学习基础知识，这一节主要将公式变为代码。 代码编写网站：https://colab.research.google.com/drive 学习课程链接：ML 2022 Spring 1、Load Data（读取数据） 这需要用到pytorch里面的两个函数Dataset和Dataloader torch.utils.data.Datase
阅读更多...
Scikit-learn (sklearn)速通 -【莫凡Python学习笔记】

Scikit-learn (sklearn)速通 -【莫凡Python学习笔记】

视频教程链接：【莫烦Python】Scikit-learn (sklearn) 优雅地学会机器学习 视频教程代码 scikit-learn官网 莫烦官网学习链接 本人matplotlib、numpy、pandas笔记 1 为什么学习 Scikit learn 也简称 sklearn, 是机器学习领域当中最知名的 python 模块之一. Sklearn 包含了很多种机器学习的方式:
阅读更多...
NOIP模拟题 by天津南开中学 莫凡[tarjan][树剖][并查集]

NOIP模拟题 by天津南开中学 莫凡[tarjan][树剖][并查集]

考试总结： 解题报告： 一． 图的连通性： 题意：给定一图，动态删边，动态求是否连通，且查询中输入的变量需xor当前边数才为最终输入数据； 分析：只删边则可以逆向建边用并查集查询是否连通，并查集基本上也是现阶段唯一一种可以在线快速求联通的算法了； 具体实现的话，先把边用康托展开转化为n+1进制的数，再用map去映射一个编号，然后两个mapy一个通过编号存储边出现次数，一个通过编号存储这条
阅读更多...
莫凡《机器学习》笔记

莫凡《机器学习》笔记

笔记参考地址：https://morvanzhou.github.io/tutorials/machine-learning/ML-intro/ 机器学习方法 1.1 机器学习 通常来说, 机器学习的方法包括: 监督学习 supervised learning：（有数据有标签）在学习过程中，不断的向计算机提供数据和这些数据对应的值，如给出猫、狗的图片并告诉计算机哪些是猫哪些是狗，让计算机去学习分
阅读更多...
【莫凡PyTorch教程笔记】-2. 建造第一个神经网络

【莫凡PyTorch教程笔记】-2. 建造第一个神经网络

关系拟合 (回归) 这次会来见证神经网络是如何通过简单的形式将一群数据用一条线条来表示. 或者说, 是如何在数据当中找到他们的关系, 然后用神经网络模型来建立一个可以代表他们关系的线条. 建立数据集 我们创建一些假数据来模拟真实的情况. 比如一个一元二次函数: y = a * x^2 + b, 我们给 y 数据加上一点噪声来更加真实的展示它. x = torch.unsqueeze(to
阅读更多...
莫凡的python_莫凡Python之keras 2

莫凡的python_莫凡Python之keras 2

莫凡Python 2 kearsregressionpython Classifier 分类 使用 mnist 数据集，这是0-9的图片数据，我们使用神经网络去识别这些图片。显示图片上的数据 本质上是使用神经网络去分类。 参考资料 数据预处理、熟悉数据 # -*- coding: utf-8 -*- """ Classifier 分类 """ from keras.datas
阅读更多...
莫凡强化学习

莫凡强化学习

课程要求 - 强化学习 (Reinforcement Learning) | 莫烦Python (mofanpy.com)    DQN Dueling DQN - 强化学习 (Reinforcement Learning) | 莫烦Python (mofanpy.com) 问题： 1.AttributeError: module 'tensorflow' has n
阅读更多...
Matplotlib-莫凡

Matplotlib-莫凡

Matplotlib是python中的画图包 安装MLP之前先安装numpy #基本用法import matplotlib.pyplot as pltimport numpy as npx=np.linspace(-1,1,50)# y=2*x+1y=x**2plt.plot(x,y)plt.show() 输出: #figure的使用,即窗口import matplotl
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2