【黏菌优化算法】基于平衡黏菌优化算法求解单目标优化问题 (ESMA)含Matlab源码

1 简介

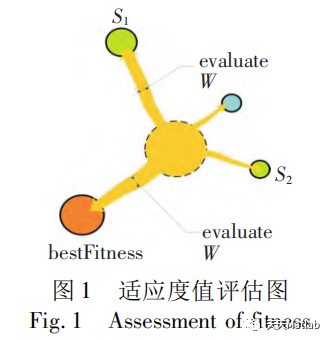
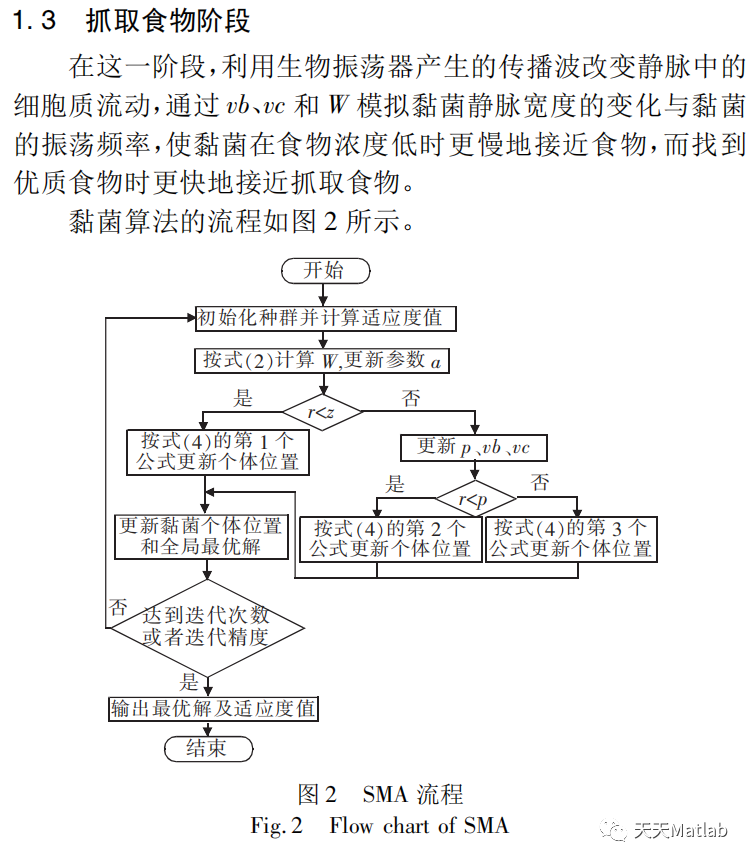
黏菌优化算法（Slime mould algorithm，SMA）由 Li等于 2020 年提出，其灵感来自于黏菌的扩散和觅食行为，属于元启发算法。具有收敛速度快，寻优能力强的特点。黏菌优化算法用数学模型模仿黏菌觅食行为和形态变化， SMA 包括三个阶段，分别为接近食物阶段、包围食物阶段和抓取食物阶段。

正在上传…重新上传取消

2 部分代码

% Equlibrium Slime Mould Algorithm (LSMA) %% Developed in MATLAB R2019b%_____________________________________________________________________________________________________​​clearvarsclose allclc​disp('The ESMA is tracking the problem');​N=20; % 粘菌数Function_name='F1' % 测试功能的名称，可以从 F1 到 F23MaxIT=200; % 最大迭代次数​[lb,ub,dim,fobj]=Get_Functions_details(Function_name); % Function details​Times=11; %您想要运行 ESMA 的独立次数display(['Number of independent runs: ', num2str(Times)]);​for i=1:Times[Destination_fitness(i),bestPositions(i,:),Convergence_curve(i,:)]=ESMA(N,MaxIT,lb,ub,dim,fobj);display(['The optimal fitness of ESMA is: ', num2str(Destination_fitness(i))]);end​[bestfitness,index]=min(Destination_fitness);disp('--------Best Fitness, Average Fitness, Standard Deviation and Best Solution--------');display(['The best fitness of ESMA is: ', num2str(bestfitness)]);display(['The average fitness of ESMA is: ', num2str(mean(Destination_fitness))]);display(['The standard deviation fitness of ESMA is: ', num2str(std(Destination_fitness))]);display(['The best location of ESMA is: ', num2str(bestPositions(index,:))]);figure('Position',[269   240   660   290])%Draw search spacesubplot(1,2,1);func_plot(Function_name);title('Parameter space')xlabel('x_1');ylabel('x_2');zlabel([Function_name,'( x_1 , x_2 )'])​%Draw objective spacesubplot(1,2,2);semilogy(Convergence_curve(index,:),'LineWidth',1);xlabel('迭代');ylabel('最优值');legend('ESMA');box on;axis tight;grid off;​

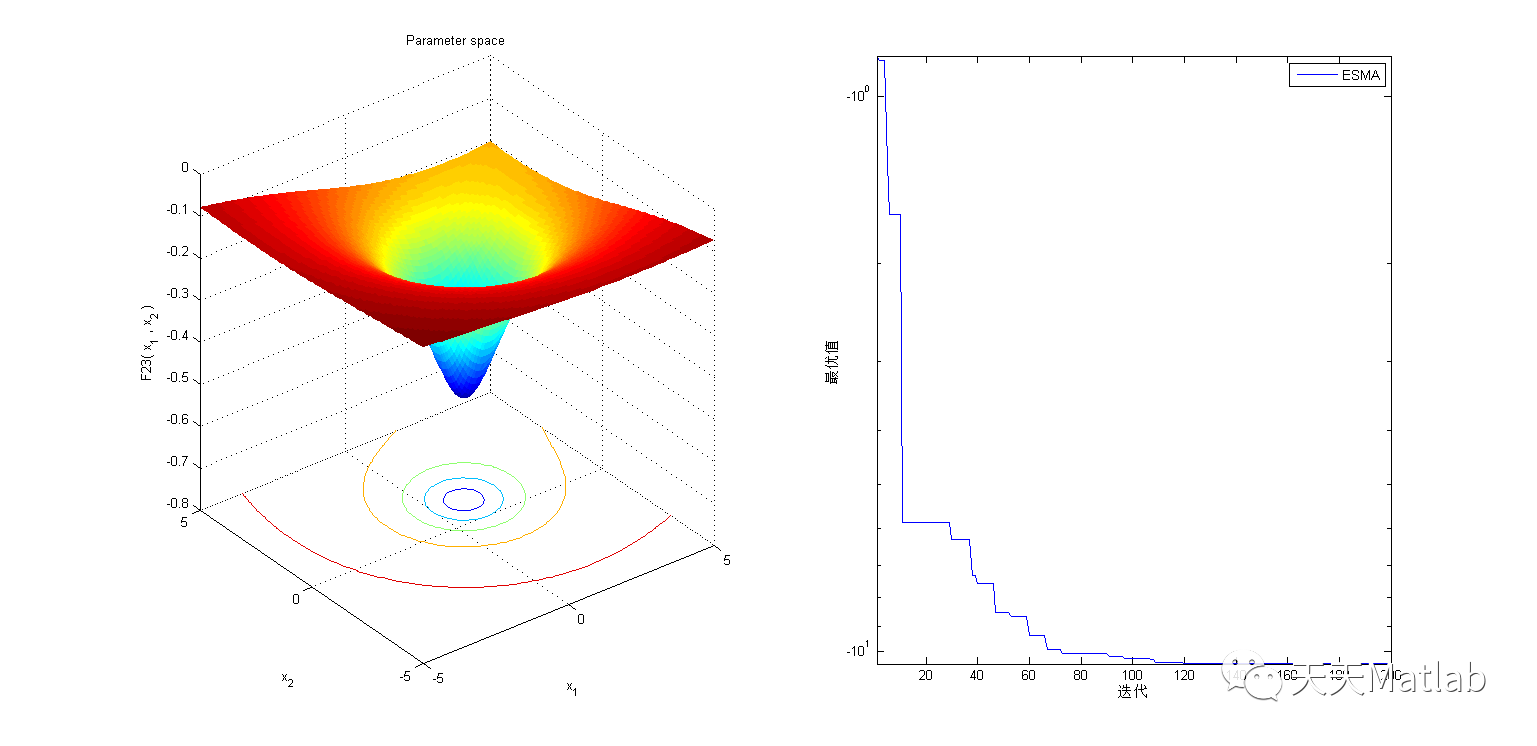
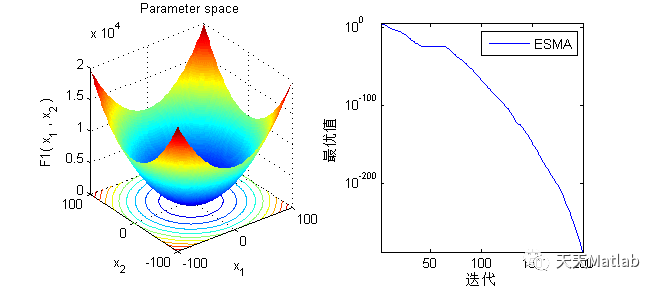
3 仿真结果

4 参考文献

[1]郭雨鑫,刘升,张磊,黄倩.精英反向与二次插值改进的黏菌算法[J/OL].计算机应用研究:1-7​

博主简介：擅长智能优化算法、神经网络预测、信号处理、元胞自动机、图像处理、路径规划、无人机等多种领域的Matlab仿真，相关matlab代码问题可私信交流。

部分理论引用网络文献，若有侵权联系博主删除。