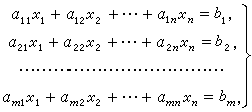[NOIP2004]虫食算高斯消元

2023-12-07 07:18

文章标签 高斯消食算 noip2004

本文主要是介绍[NOIP2004]虫食算高斯消元，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

网上的题解各种坑真是尴尬搞了好久现在弄懂了

给出样例

5
ABCED
BDACE
EBBAA

废话不多说乱枚举肯定超时作如下处理

设

D + E - A = d1

C + E - A = -d1 + d2

C + A - B = -d2 + d3

B + D - B = -d3 + d4</

这篇关于[NOIP2004]虫食算高斯消元的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

http://www.chinasem.cn/article/464969。 23002807@qq.com

HDU 5833 高斯消元

n个数，任选>=1个数相乘，使得乘积是完全平方数。其实就是开关，控制灯泡。数 ----第i个质因子p的个数%2 = {1 ， 0} == 开关----第i个灯泡 = {开，关} 最后使得所有灯泡都是灭着的方案数 = 2^自由变元个数全部关着的情况 == 一个数也不选应省去 import java.io.BufferedReader;

hiho一下第56周高斯消元

小Ho：<吧唧><吧唧><吧唧> 小Hi：小Ho，你还吃呢。想好了么? 小Ho：肿抢着呢(正想着呢)...<吞咽>...我记得这个问题上课有提到过，应该是一元一次方程组吧。我们把每一件商品的价格看作是x[1]..x[n]，第i个组合中第j件商品数量记为a[i][j]，其价格记作y[i]，则可以列出方程式： a[1][1] * x[1] + a[1][2] * x[2] + ... +

poj 1222 EXTENDED LIGHTS OUT (高斯消元解异或方程组开关问题)

近距离观摩今天北京站的比赛，向志愿者学姐要了一份题目，看了看H题；因为数据被弱化，瞬间就想到了背包；就先研究下标准解法——异或方程组；下面为转载文：题意：有一个5*6的矩阵，每个位置都表示按钮和灯，1表示亮，0表示灭。每当按下一个位置的按钮，它和它周围灯的状态全部翻转，问在这样的一个方阵中按下哪些按钮可以把整个方阵都变成灭的，这时1表示按了，0表示没按。以下

poj1681 高斯消元+dfs枚举

wa N多次后，终于把高斯消元的模板给弄出来了，并且精简了许多。用dfs枚举变元比二进制枚举变元简单多了。（也终于明白变元代表只得解的个数。）上模板。 #include <iostream>#include <algorithm>using namespace std;int a[400][400];int ans[400],x[400];//ans[]用于记录哪几种

poj1222 枚举和高斯消元

接触开关问题，最先的方法是枚举。然后接触到了更加高深的高斯消元。高斯消元的思想：把一个全部熄灭的矩阵经过一系列开关后得到初始的状态。具体分析可参照 http://blog.csdn.net/shiren_Bod/article/details/5766907 下面附上的代码付注释： #include <iostream>using namespace std;int map[3

洛谷：P1085 [NOIP2004 普及组] 不高兴的津津

1. 题目链接 https://www.luogu.com.cn/problem/P1085 P1085 [NOIP2004 普及组] 不高兴的津津 2. 题目描述题目描述：津津每天要上课还要上辅导班，每天学习超过8小时就不开心，帮忙检查下津津的下周日程安排，然后告诉我她哪天不高兴输入：7行数据，每行2个小于10的非负整数，分别代表在学校的时间和辅导班的时间输出：哪天最不高兴，如果有

AcWing算法基础课笔记——高斯消元

高斯消元用来求解方程组 a 11 x 1 + a 12 x 2 + ⋯ + a 1 n x n = b 1 a 21 x 1 + a 22 x 2 + ⋯ + a 2 n x n = b 2 … a n 1 x 1 + a n 2 x 2 + ⋯ + a n n x n = b n a_{11} x_1 + a_{12} x_2 + \dots + a_{1n} x_n = b_1\\ a_

【C++】高斯消元算法

矩阵初等行变换法则任一行可以与另一行进行加减。任一行可以乘或除以一个非零常数（除其实就是乘一个倒数）。任两行可以交换位置。线性方程组形如 a 1 , 1 x 1 + a 1 , 2 x 2 + ⋯ + a 1 , n x n = b 1 a 2 , 1 x 1 + a 2 , 2 x 2 + ⋯ + a 2 , n x n = b n ⋮ a n , 1 x 1 + a n , 2

To xor or not to xor 高斯消元求异或

【题目】给你n个long long范围内的整数，你可以选取1个或多个数进行异或操作，使得结果最大，求最大的结果。【题目分析】真是一道好题，不是真正理解高斯消元是无法做这题的。题意：给你n个数，可以选择任意个数异或，但是要使得最后的异或值最大。我们把每个数用二进制表示，要使得最后的异或值最大，就是要让高位尽量为1，高位能不能为1就必须用高斯消元判断了。 1. 根据数的二进制表示，建立

UVA 1564 - Widget Factory（高斯消元)

UVA 1564 - Widget Factory 题目链接题意：n种零件, 给定m个制作时间，每段时间制作k个零件，每种零件有一个制作时间，每段时间用Mon到Sun表示，求每个零件的制作时间，还要判断一下多解和无解的情况思路：对于每段时间列出一个方程，这样一共列出m个方程解n个变元，利用高斯消元去求解，注意每个方程都是MOD 7的，所以在高斯消元过程中遇到除法要求该数字%7的逆

[NOIP2004]虫食算 高斯消元

相关文章

[NOIP2004]虫食算高斯消元