三种策略改进的沙猫群优化算法(MSCSO)，与白鲸、蜣螂、麻雀等多种算法进行比较，MATLAB代码...

沙猫群优化算法(sand cat swarm optimiza⁃ tion,SCSO)是 2022年提出的元启发式优化算法，该算法灵感来源于沙猫的捕食行为，沙猫群会通过搜索阶段和捕食阶段获得食物。其中算法额外使用自适应的rG和R以达到搜索阶段和捕食阶段的无缝 切换。该算法具有寻优能力强、收敛速度快等特点，但仍存在全局探索能力较弱、算法后期易陷入局部最优等缺点。

此文复现一篇于2022年十月由Di Wu提出的沙猫群优化算法(MSCSO)，文献采用三种策略对SCSO算法进行改进：三角形游走策略、Levy飞行游走策略、透镜成像反向学习。三种策略同样适合改进其他任意的智能优化算法。

Part 1 SCSO原理介绍

• 种群初始化

与所有的元启发式优化算法一样，SCSO算法首先在范围内生成一个均匀分布的随机种群。初始化的具体的公式为：

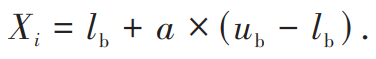
• 搜索阶段

沙猫的猎物搜索机制依赖于低频噪声发射 .每只沙猫的表达式为 Xi=(xi1,xi2,xi3,⋯,xid )。前面提到，沙猫可以感知低于2 kHz的低频，在数学模型中，这个值将随着迭代过程的进行从2线性地降低为0，以达到逐渐靠近猎物而不会丢失或跳过的作用。因此为了搜索猎物，假设沙猫的敏感范围为2 kHz到0，SM 模拟了沙猫的听觉特性，其值为2，即

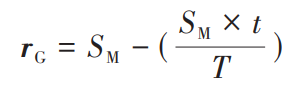
其中：t是当前迭代次数；T是最大迭代次数。在搜索步骤中，每个当前搜索代理的位置更新都是基于一个随机位置.这样，搜索代理就能够在搜索空间中探索新的空间。为避免陷入局部最优，每只沙猫的灵敏度范围是不同的，即

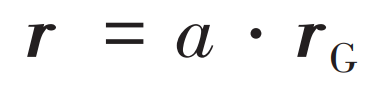
每只沙猫会根据最优解Pbc、自己当前位置Pc和其灵敏度范围r 更新自己的位置.因此沙猫能找到其他最好的猎物位置，新的位置位于当前位置和猎物位置之间，同时随机性保证了算法的低运行成本和低复杂度。

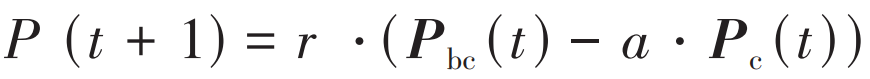
• 捕食阶段

最优位置Pb与当前位置Pc的距离的计算式为：

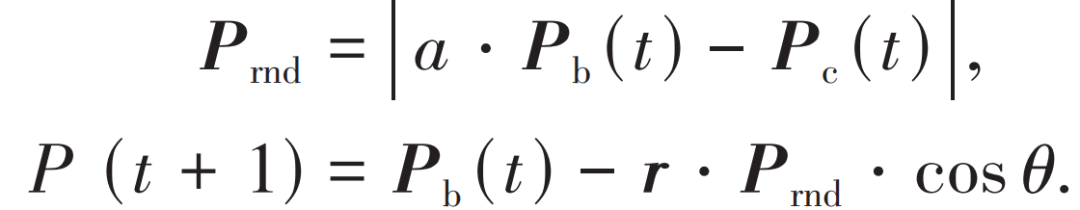
同时假设沙猫的灵敏度范围是一个圆，这样移动的方向就可以通过圆上的一个随机角度θ确定。由于所选的随机角度在0°到360°之间，所以其值将在−1到1之间。群体中的每个成员都能够在搜索空间中沿着不同的圆周方向移动，移动的距离为Pmd。SCSO算法利用轮盘选择算法为每只沙猫选择一个随机角度，用这种方法，沙猫可以接近狩猎位置，从而达到避免陷入局部最优的效果。迭代过程中的位置更新如图。

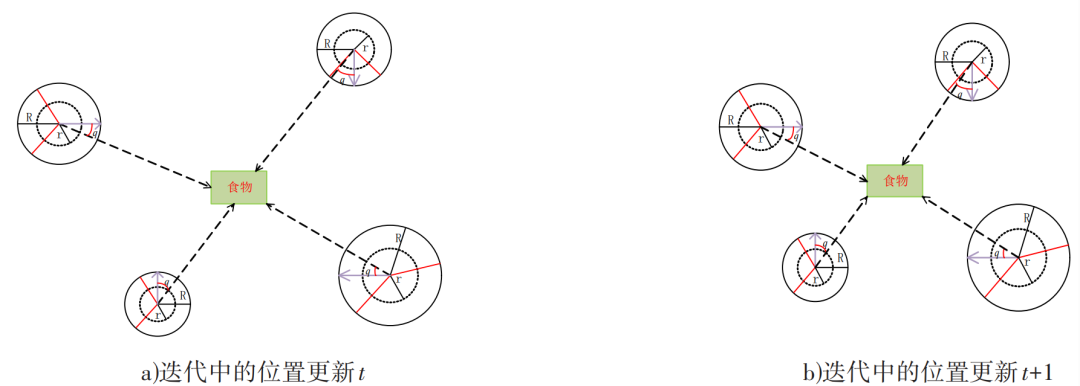
• 平衡机制 

控制搜索阶段和捕食阶段之间转换的主要参数是R，其允许SCSO在两个阶段之间无缝切换。当|R|≤1时，沙猫的下一个位置可以是当前位置与狩猎位置之间的任意位置，否则沙猫的任务是在全局寻找一种新的可能的解决方案 。R和X(t+1)计算式为：

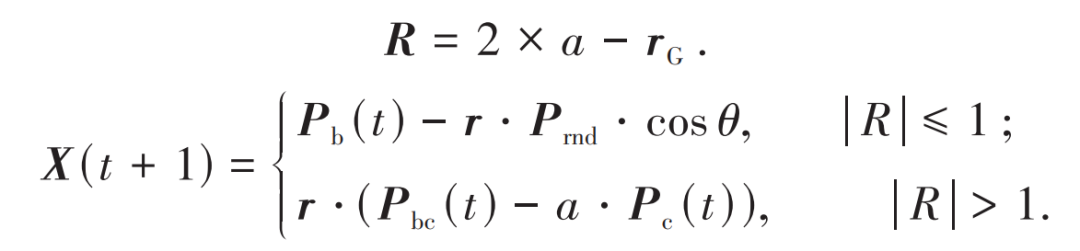
Part 2 改进策略原理介绍

• 三角形游走策略

在沙猫进行搜索过程中，沙猫会逐渐的向猎物靠近。三角游走策略是沙猫在靠近猎物的同时在周围进行游走。首先，得到沙猫和猎物之间的距离L1，在获得沙猫游走的步长范围L2。

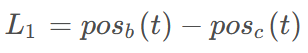
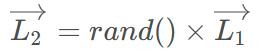
之后，根据下述公式定义行走的方向。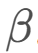

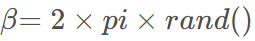
再采用下述公式求出获得沙猫游走后得到的位置。

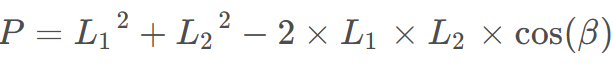
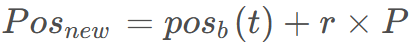
• Levy飞行游走策略

在攻击猎物时，沙猫与猎物的距离十分的接近。Levy飞行是一种非常有效的提供随机因子的数学方法。Levy飞行可以提供步长符合Levy分布的随机游走方法。但Levy飞行有时步长过长，为了更加符合沙猫攻击猎物的行为，在Levy飞行乘以常数 C=0.35，从而减少步长，使沙猫尽可能在猎物旁边进行游走。Levy飞行游走策略的公式如下所示。

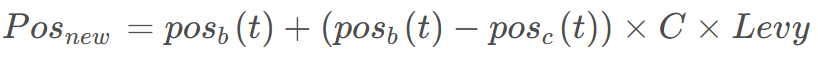
• 透镜成像反向学习策略

透镜成像反向学习主要的思想是以当前坐标为基准通过凸透镜成像的原理生成一个反向位置来扩大搜索范围，这样可以既能跳出当前位置，又可以扩大搜索范围，提高了种群的多样性。基于透镜成像原理的反向学习公式如下：

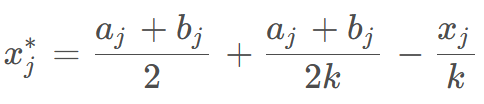
Part 3 结果展示

同样是在CEC2005函数集上进行测试，将改进的沙猫群优化算法(MSCSO)与白鲸优化算法(BWO)，蜣螂优化算法(DBO)，麻雀优化算法(SSA)，霜冰优化算法(RIME)，沙猫群优化算法(SCSO)共六种优化算法进行对比。实验结果如下：

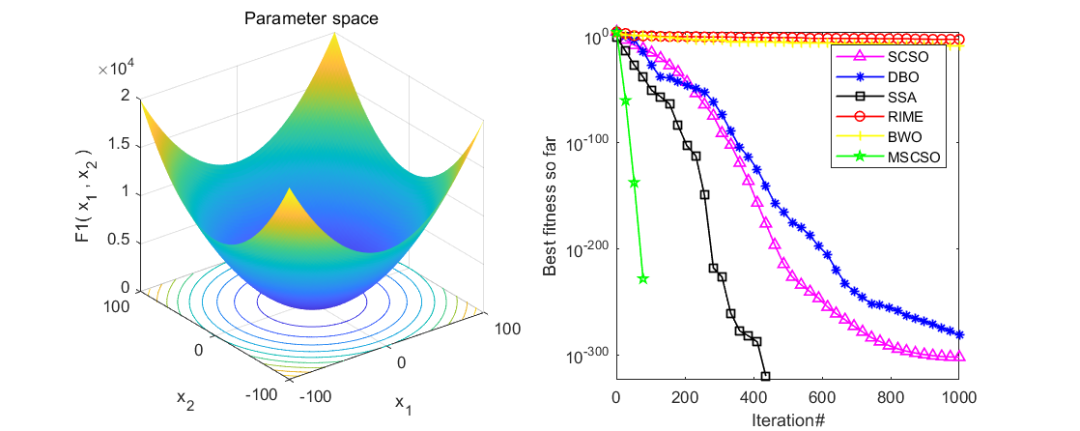
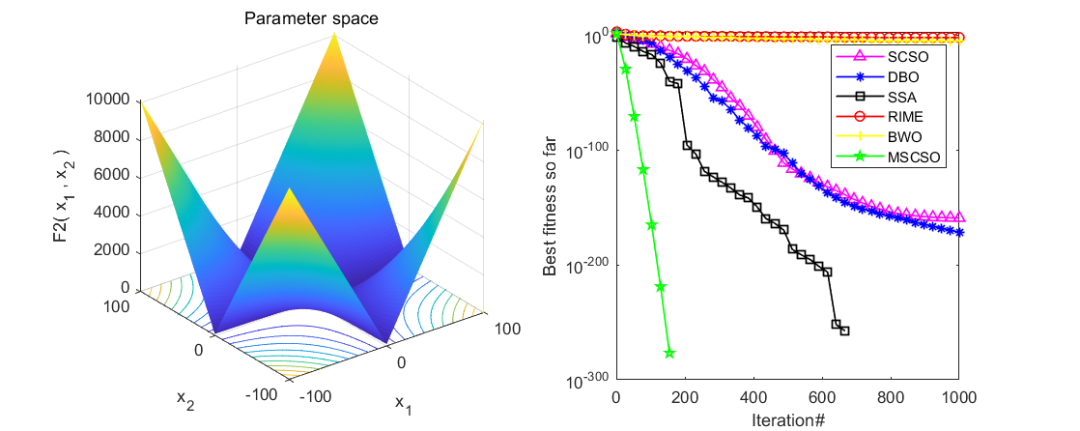
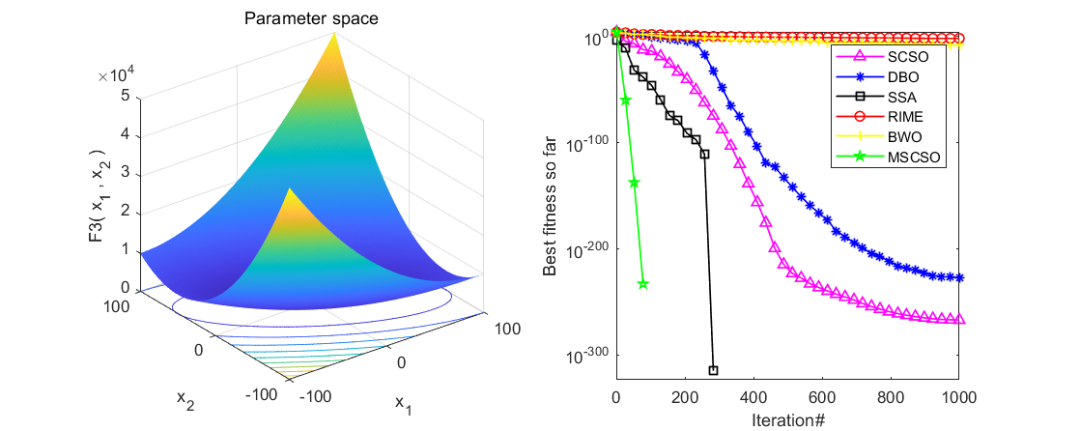
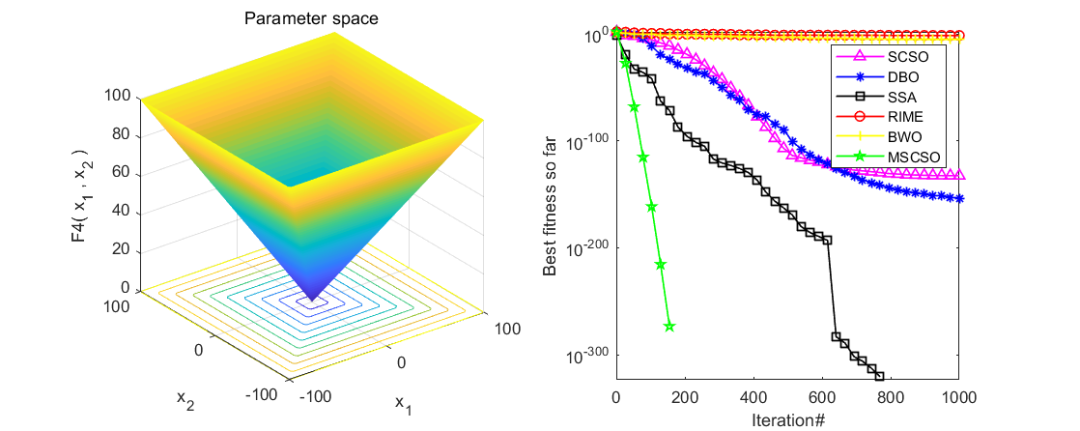
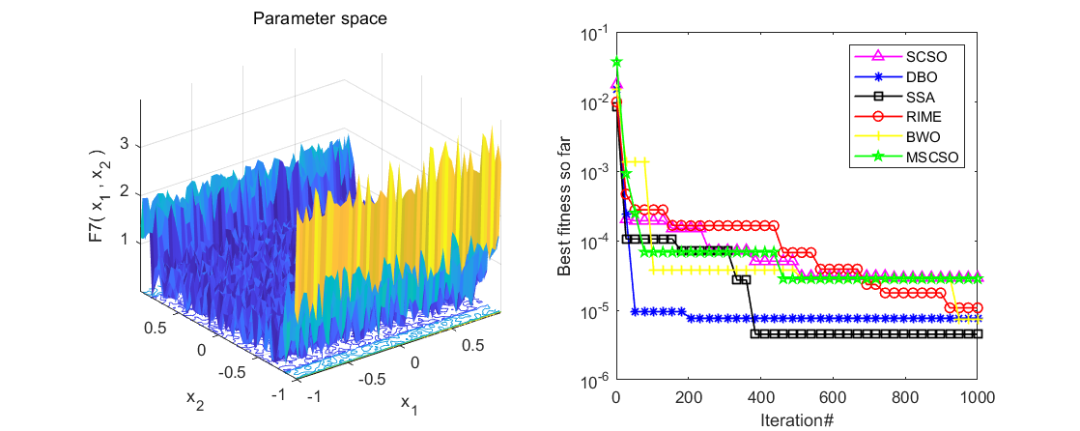
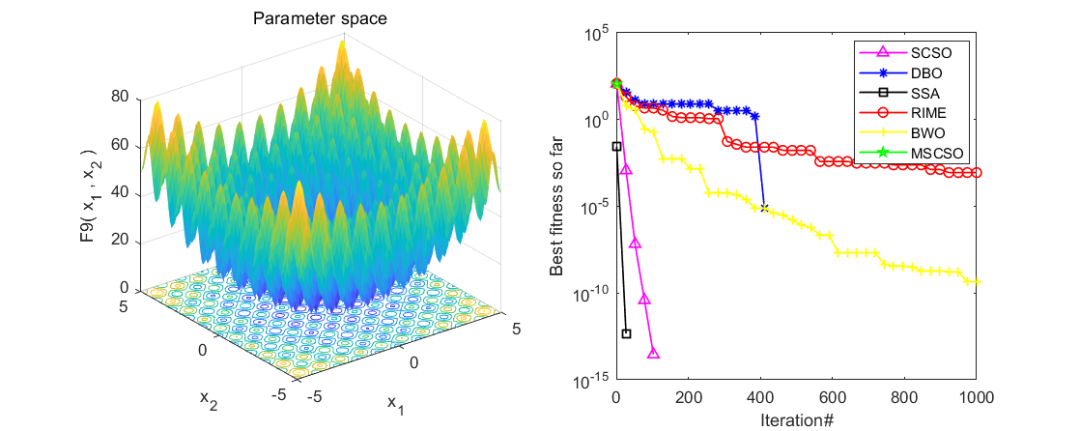
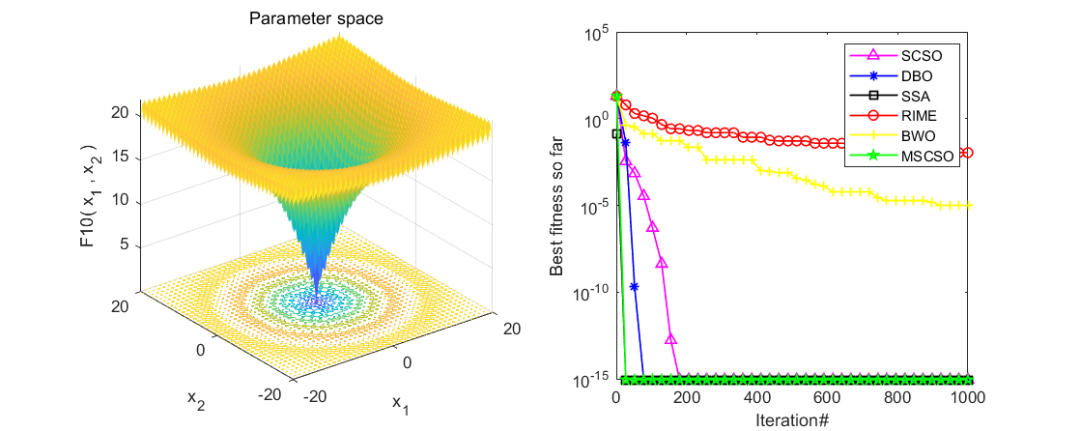
随机挑选了几个函数，经过测试效果还是相当不错的，经受住了来自五种算法的考验。

Part 4 代码展示

clear all 
clcPD_no=100;      %Number of sand cat
F_name='F2';     %Name of the test function
Max_iter=1000;    %Maximum number of iterations
[LB,UB,Dim,F_obj]=CEC2005(F_name); %Get details of the benchmark functions%% BWO    
[Best_pos,Best_score, BWO_cg_curve ] = BWO(PD_no,Max_iter,LB,UB,Dim,F_obj); % Call BWO
fprintf ('Best solution obtained by BWO: %s\n', num2str(Best_score,'%e  '));
display(['The best optimal value of the objective funciton found by BWO  for ' [num2str(F_name)],'  is : ', num2str(Best_pos)]);%% DBO    
[Best_pos,Best_score, DBO_cg_curve ] = DBO(PD_no,Max_iter,LB,UB,Dim,F_obj); % Call DBO
fprintf ('Best solution obtained by DBO: %s\n', num2str(Best_score,'%e  '));
display(['The best optimal value of the objective funciton found by DBO  for ' [num2str(F_name)],'  is : ', num2str(Best_pos)]);%% SSA    
[Best_pos,Best_score, SSA_cg_curve ] = SSA(PD_no,Max_iter,LB,UB,Dim,F_obj); % Call SSA
fprintf ('Best solution obtained by SSA: %s\n', num2str(Best_score,'%e  '));
display(['The best optimal value of the objective funciton found by SSA  for ' [num2str(F_name)],'  is : ', num2str(Best_pos)]);%% RIME    
[Best_pos,Best_score, RIME_cg_curve ] = RIME(PD_no,Max_iter,LB,UB,Dim,F_obj); % Call RIME
fprintf ('Best solution obtained by RIME: %s\n', num2str(Best_score,'%e  '));
display(['The best optimal value of the objective funciton found by RIME  for ' [num2str(F_name)],'  is : ', num2str(Best_pos)]);%% SCSO
[BsSCSO,BpSCSO,SCSO_cg_curve]=SCSO(PD_no,Max_iter,LB,UB,Dim,F_obj); % Call MSCSO
fprintf ('Best solution obtained by SCSO: %s\n', num2str(BsSCSO,'%e  '));
display(['The best optimal value of the objective funciton found by SCSO  for ' [num2str(F_name)],'  is : ', num2str(BpSCSO)]);%% MSCSO
[Best_PD,PDBest_P,MSCSO_cg_curve]=MSCSO(PD_no,Max_iter,LB,UB,Dim,F_obj); % Call MSCSO
fprintf ('Best solution obtained by MSCSO: %s\n', num2str(Best_PD,'%e  '));
display(['The best optimal value of the objective funciton found by MSCSO  for ' [num2str(F_name)],'  is : ', num2str(PDBest_P)]);CNT=40;
k=round(linspace(1,Max_iter,CNT)); %随机选CNT个点
% 注意：如果收敛曲线画出来的点很少，随机点很稀疏，说明点取少了，这时应增加取点的数量，100、200、300等，逐渐增加
% 相反，如果收敛曲线上的随机点非常密集，说明点取多了，此时要减少取点数量
iter=1:1:Max_iter;
figure('Position',[154   145   894   357]);
subplot(1,2,1);
func_plot(F_name);     % Function plot
title('Parameter space')
xlabel('x_1');
ylabel('x_2');
zlabel([F_name,'( x_1 , x_2 )'])
subplot(1,2,2);       % Convergence plot
h1 = semilogy(iter(k),SCSO_cg_curve(k),'m-^','linewidth',1);
hold on
h2 = semilogy(iter(k),DBO_cg_curve(k),'b-*','linewidth',1);
hold on
h3 = semilogy(iter(k),SSA_cg_curve(k),'k-s','linewidth',1);
hold on
h4 = semilogy(iter(k),RIME_cg_curve(k),'r-o','linewidth',1);
hold on
h5 = semilogy(iter(k),BWO_cg_curve(k),'y-+','linewidth',1);
hold on
h6 = semilogy(iter(k),MSCSO_cg_curve(k),'g-p','linewidth',1);
xlabel('Iteration#');
ylabel('Best fitness so far');
legend('SCSO','DBO','SSA','RIME','BWO','MSCSO');

参考文献

[1] Di Wu, Honghua Rao, Changsheng Wen, et al. Modified Sand Cat Swarm Optimization Algorithm for SolvingConstrained Engineering Optimization Problems[J]. Mathematics. 2022, 10(22), 4350.

[2]贾鹤鸣,王琢,文昌盛等.改进沙猫群优化算法的无人机三维路径规划[J].宁德师范学院学报(自然科学版),2023,35(02):171-179.

完整代码获取方式：点击下方卡片，后台回复关键字，不区分大小写

关键字：MSCSO