机器学习9—关联分析之Apriori算法和FP-Growth算法

一、Apriori算法

在机器学习中，除了聚类算法外，Aprior算法也是在数据集中寻找数据之间的某种关联关系，通过该算法，我们可以在大规模的数据中发现有价值的价值，比如著名的啤酒与尿布的案例就是一种关联分析。

1.1Apriori算法原理

1.项集

• 项集是项的集合，包含k个项的集合称为k项集，如{啤酒，尿布}就是个2项集。
• 项集在所有事务中出现的次数总和称为绝对支持度或支持度计数。
• 频繁项集：某项集的支持度计算满足预定的要求即称该项集为频繁项集。

2.关联规则

• 根据频繁项集挖掘出的结果，例如 {尿布}→{啤酒}，规则的左侧称为先导，右侧称为后继
• 支持度：项集A和B的支持度被定义为数据集中同时包含这两项集的记录所占的比例。（通俗理解，就是事件A和B同时发生的概率），记做：Support(A=>B)=P(A∪B)
• 可信度（置信度）：项集A发生，则项集B发生的概率为关联规则的置信度（通俗理解,在A发生的情况下B发生的概率为多少P（B/A））记做：C o n f i d e n c e ( A = > B ) = P ( B ∣ A )

3.最小支持度和最小置信度

• 最小支持度：即衡量支持度的一个阈值，表示项集之间的支持度满足该阈值才能证明该支持度有效。
• 最小置信度：即衡量置信度的一个阈值，表示项集之间的置信度满足该阈值才能证明该置信度有效。
• 强规则：同时满足最小支持度和最小置信度规则的规则。

4.支持度计数

• 项集A的支持度计数是事务数据集中包含项集A的事务个数，简称项集的频率或计数
• 一旦得到项集A 、 B 和 A ∪ B 的支持度计数以及所有事务个数，就可以导出对应的关联规则A = > B和B = > A，并可以检查该规则是否为强规则。

• 其中N表示总事务个数，σ表示计数；support可以理解为A,B同时发生的概率，confidence可以理解为条件概率。

1.2Apriori算法实例

关联挖掘的步骤也就只有两个：第一步是找出频繁项集，第二步是从频繁项集中提取规则。

Apriori 算法的核心就是：如果某个项集是频繁项集，那么它的全部子集也都是频繁项集。
Ariori算法有两个主要步骤：

• 以餐饮行业点餐数据为例，首先先将事务数据整理成关联规则模型所需的数据结构。设最小支持度为0.2，将菜品id编号。
  
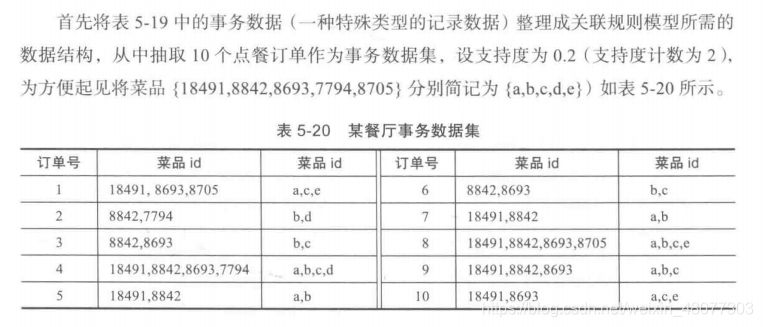
  计算 1项集，2项集，3项集
  
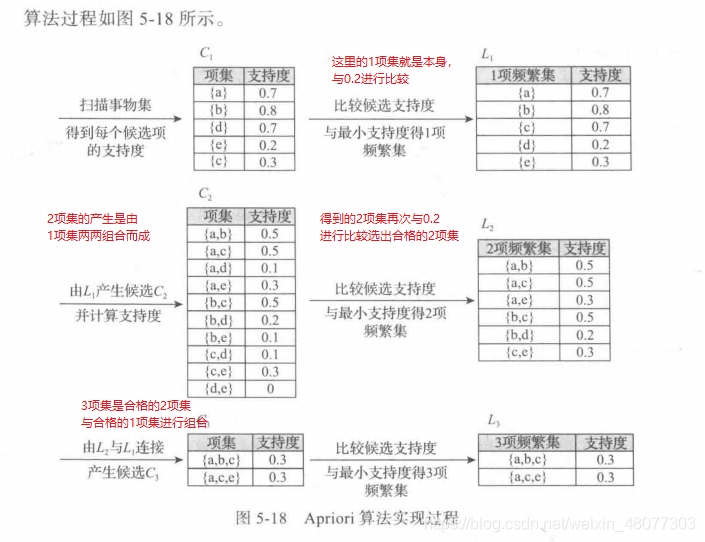
  简述过程：
  
  
  

1.3Apriori算法实例代码演示（用python来写）

import numpy as np
import pandas as pddef connect_string(x, ms):"""与1项频繁集连接生成新的项集:param x: 项集:param ms::return: 新的项集"""x = list(map(lambda i: sorted(i.split(ms)), x)) # 将排序得到的i转为列表赋予xl = len(x[0])r = []for i in range(len(x)):for j in range(i, len(x)):if x[i][:l - 1] == x[j][:l - 1] and x[i][l - 1] != x[j][l - 1]:r.append(x[i][:l - 1] + sorted([x[j][l - 1], x[i][l - 1]]))return rdef find_rule(d, support, confidence, ms=u'-'):"""寻找关联规则:param d: 数据集:param support: 最小支持度:param confidence: 最小置信度:param ms: 项集之间连接符号:return: 强关联规则以及其支持度与置信度"""# 存储输出结果result = pd.DataFrame(index=['support', 'confidence'])# 1项集的支持度序列support_series = 1.0 * d.sum(axis=0) / d.shape[0]# 基于给定的最小支持度进行筛选,得到1项频繁集column = list(support_series[support_series > support].index)# 当1项频繁集个数大于1时k = 0while len(column) > 1:k = k + 1print(u'\n正在进行第%s次搜索...' % k)column = connect_string(column, ms)print(u'数目：%s...' % len(column))# 乘积为1表示两个项集同时发生，乘积为0表示不同发生sf = lambda i: d[i].prod(axis=1, numeric_only=True)  # 新一批支持度的计算函数# 创建连接数据，这一步耗时、耗内存最严重。当数据集较大时，可以考虑并行运算优化。d_2 = pd.DataFrame(list(map(sf, column)), index=[ms.join(i) for i in column]).T# 计算连接后的支持度support_series_2 = 1.0 * d_2[[ms.join(i) for i in column]].sum() / len(d)column = list(support_series_2[support_series_2 > support].index)  # 新一轮支持度筛选support_series = support_series.append(support_series_2)column2 = []# 遍历可能的推理，如{A,B,C}究竟是A+B-->C还是B+C-->A还是C+A-->B？for i in column:i = i.split(ms)for j in range(len(i)):column2.append(i[:j] + i[j + 1:] + i[j:j + 1])# 定义置信度序列cofidence_series = pd.Series(index=[ms.join(i) for i in column2])# 计算置信度序列for i in column2:cofidence_series[ms.join(i)] = support_series[ms.join(sorted(i))] / support_series[ms.join(i[:len(i) - 1])]for i in cofidence_series[cofidence_series > confidence].index:  # 置信度筛选result[i] = 0.0result[i]['confidence'] = cofidence_series[i]result[i]['support'] = support_series[ms.join(sorted(i.split(ms)))]result = result.T.sort_values(['confidence', 'support'], ascending=False)  # 结果整理，输出print(u'\n结果为：')print(result)return resultif __name__ == '__main__':# 加载数据data = pd.read_csv('menu_orders.csv', header=None)print('转换原数据到0-1矩阵')ct = lambda x: pd.Series(1, index=x[pd.notnull(x)])b = map(ct, data.values)data = pd.DataFrame(list(b)).fillna(0)# 删除中间变量bdel bsupport = 0.2  # 最小支持度confidence = 0.5  # 最小置信度find_rule(data, support, confidence) # 函数调用

输出为：

转换原数据到0-1矩阵正在进行第1次搜索...
数目：6...正在进行第2次搜索...
数目：3...正在进行第3次搜索...
数目：0...结果为：support  confidence
e-a        0.3    1.000000
e-c        0.3    1.000000
c-e-a      0.3    1.000000
a-e-c      0.3    1.000000
c-a        0.5    0.714286
a-c        0.5    0.714286
a-b        0.5    0.714286
c-b        0.5    0.714286
b-a        0.5    0.625000
b-c        0.5    0.625000
a-c-e      0.3    0.600000
b-c-a      0.3    0.600000
a-c-b      0.3    0.600000
a-b-c      0.3    0.600000

1.4Apriori算法中apriori()函数使用

机器sklearn包中并无efficient_apriori 工具，所以要对efficient_apriori 下载。
首先：

pip install apyori

其次：

pip install efficient-apriori

Apriori算法中apriori()函数的构造形式为：

apriori(transactions: Iterable[Union[set, tuple, list]], min_support: float = 0.5, min_confidence: float = 0.5, max_length: int = 8, verbosity: int = 0, output_transaction_ids: bool = False)

参数说明：

• transactions：在set, tuple, list中中的每个元素交易必须是可散列的。
• min_support：float型，默认0.5值。一个介于 0 和 1 之间的浮点数，用于返回的项集的最小支持度。
• min_confidence：float型，返回的规则的最小置信度。给定规则 X -> Y，则置信度是给定 X 的 Y 的概率，即 P(Y|X) = confidence(X -> Y)
• max_length: int型，项目集和规则的最大长度。
• verbosity: int型，打印显示迭代次数。如 0、1 或 2。
• output_transaction_ids: bool型，默认False。如果为True ，则在返回的数据帧中使用数据帧的列名，而不是列索引。

Apriori算法的简单使用：

from efficient_apriori import apriori# 设置数据集
data = [('尿布', '啤酒', '奶粉', '洋葱'),('尿布', '啤酒', '奶粉', '洋葱'),('尿布', '啤酒', '苹果', '洋葱'),('尿布', '啤酒', '苹果'),('尿布', '啤酒', '奶粉'),('尿布', '啤酒', '奶粉'),('尿布', '啤酒', '苹果'),('尿布', '啤酒', '苹果'),('尿布', '奶粉', '洋葱'),('奶粉', '洋葱')]
# 挖掘频繁项集和规则
itemsets, rules = apriori(data, min_support=0.4, min_confidence=1)# 最小支持度为0.4，最小置信度为1
print('频繁项目集为')
print(itemsets)
print('规则为')
print(rules)

输出：

频繁项目集为
{1: {('尿布',): 9, ('啤酒',): 8, ('奶粉',): 6, ('洋葱',): 5, ('苹果',): 4}, 2: {('啤酒', '奶粉'): 4, ('啤酒', '尿布'): 8, ('啤酒', '苹果'): 4, ('奶粉', '尿布'): 5, ('奶粉', '洋葱'): 4, ('尿布', '洋葱'): 4, ('尿布', '苹果'): 4}, 3: {('啤酒', '奶粉', '尿布'): 4, ('啤酒', '尿布', '苹果'): 4}}
规则为
[{啤酒} -> {尿布}, {苹果} -> {啤酒}, {苹果} -> {尿布}, {啤酒, 奶粉} -> {尿布}, {尿布, 苹果} -> {啤酒}, {啤酒, 苹果} -> {尿布}, {苹果} -> {啤酒, 尿布}]

二、FP-Growth算法

2.1FP-Growth算法概述

FpGrowth算法通过构造一个树结构来压缩数据记录，使得挖掘频繁项集只需要扫描两次数据记录，而且该算法不需要生成候选集合，所以效率会比较高。

• FP-Tree（频繁模式树）：是一个树形结构，包括一个频繁项组成的头表，一个标记为null的根结点，它的子结点为一个项前缀子树的集合。
• 频繁项：单个项目的支持度超过最小支持度则称其为频繁项（frequentitem）。
• 频繁头表：频繁项头表的每个表项由两个域组成，一个是项目名称，一个是链表指针，指向下一个相同项目名称的结点。
• 生成FP-Growth树

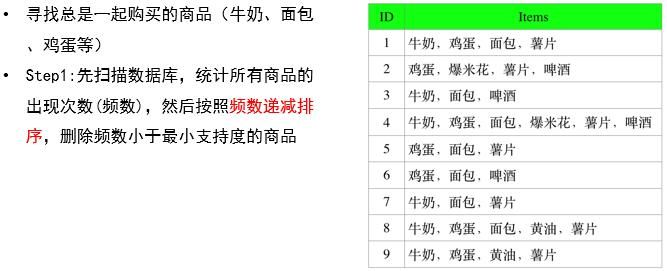
1、遍历数据集，统计各元素项出现次数，创建头指针表

2、移除头指针表中不满足最小值尺度的元素项

3、第二次遍历数据集，创建FP树。对每个数据集中的项集：

3.1 初始化空FP树
3.2 对每个项集进行过滤和重排序
3.3 使用这个项集更新FP树，从FP树的根节点开始：
3.3.1 如果当前项集的第一个元素项存在于FP树当前节点的子节点中，则更新这个子节点的计数值
3.3.2 否则，创建新的子节点，更新头指针表
3.3.3 对当前项集的其余元素项和当前元素项的对应子节点递归3.3的过程

2.2FP-Growth算法的特点

• 相比Apriori算法需要多次扫描数据库，FPGrowth只需要对数据库扫描2次。
• 第1次扫描事务数据库获得频繁1项集。
• 第2次扫描建立一颗FP-Tree树。

2.3FP-Growth算法的原理

• 频繁项集
  

• 统计频次和降序排序
  

• 重新排序:Step2:对每一条数据记录，按照F1重新排序。
  

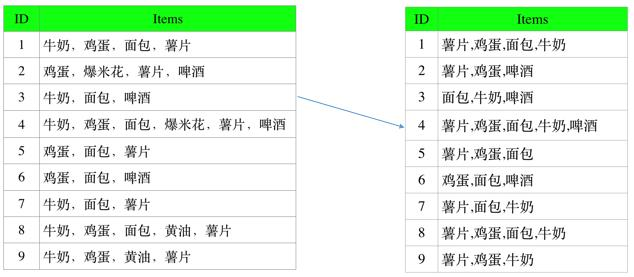
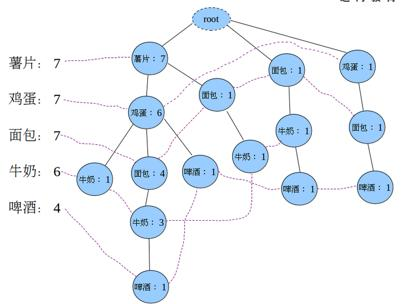
• 建立FP树：
  Step3：把Step2重新排序后的记录，插入到fp-tree中
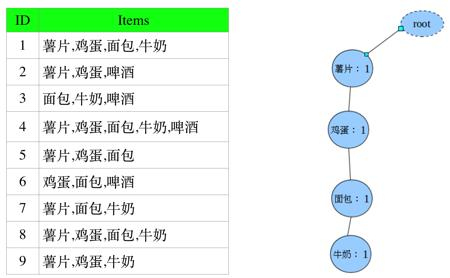
  Step3.1：插入第一条（第一步有一个虚的根节点root）
  
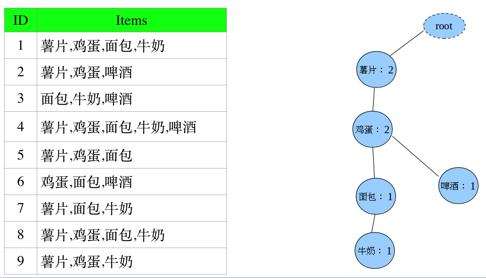
  Step3.2：插入第二条。根结点不管，然后薯片在step3.1的基础上+1，则记为2；同理鸡蛋记为2；啤酒在step3.1的树上是没有的，就另开一个分支。
  
  Step3.3：插入第三条，由于起点不是以薯片为开始，而是面包故在虚节点为根节点另起一个分支。
  
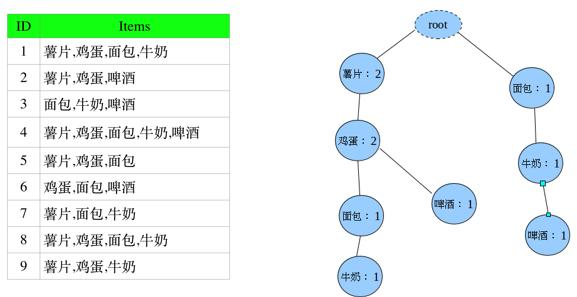
  同理，剩余记录依次插入FP-tree，可得：
  

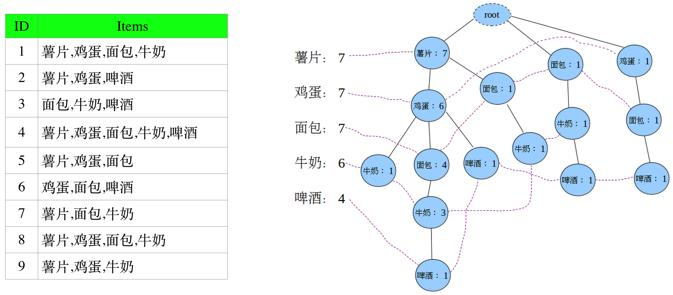
图中左边的一列叫做头指针表，树中相同名称的节点要链接起来，链表的第一个元素就是头指针表里的元素。
虚线相连的表示同一个商品，各个连接的数字加起来就是该商品出现的总次数。

Step4：从FP-Tree中找出频繁项集，对于每一条路径上的节点，其count都设置为牛奶的count（路径中最末尾的商品数）。

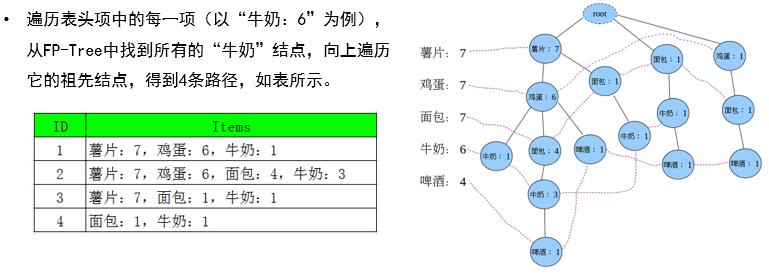
因为每一项末尾都是牛奶，可以把牛奶去掉，得到条件模式基，此时的后缀模式是：牛奶。

2.4FP-Growth算法中函数fpgrowth()的使用

fpgrowth(df, min_support=0.5, use_colnames=False, max_len=None, verbose=0)

参数说明：

• df： pandas DataFrame 编码格式。还支持具有稀疏数据的 DataFrame。DataFrame中允许的值为 0/1 或 True/False。
• min_support：float (默认0.5)。一个介于 0 和 1 之间的浮点数，用于对返回的项目集的最小支持度。
• use_colnames： bool (默认False)。如果为 true，则在返回的 DataFrame 中使用 DataFrame 的列名而不是列索引。
• max_len： int (默认None)。生成的项目集的最大长度。如果是“None”（默认）则评估所有可能的项集长度。
• verbose：int (默认0)。来显示条件树生成的阶段。

上述购买商品实例用FP-Growth算法来分析：

import pandas as pd
from mlxtend.preprocessing import TransactionEncoder
from mlxtend.frequent_patterns import fpgrowth
from mlxtend.frequent_patterns import association_rules # 生成强关联规则data_test = [['A', 'C', 'D'], ['B', 'C', 'E'], ['A', 'B', 'C', 'E'], ['B', 'E']]def create_data():dataset = [['Milk', 'Onion', 'Nutmeg', 'Kidney Beans', 'Eggs', 'Yogurt'],['Dill', 'Onion', 'Nutmeg', 'Kidney Beans', 'Eggs', 'Yogurt'],['Milk', 'Apple', 'Kidney Beans', 'Eggs'],['Milk', 'Unicorn', 'Corn', 'Kidney Beans', 'Yogurt'],['Corn', 'Onion', 'Onion', 'Kidney Beans', 'Ice cream', 'Eggs']]return datasetdef main():dataset = create_data()te = TransactionEncoder()# 进行 one-hot 编码te_ary = te.fit(dataset).transform(dataset)# print(te_ary)df = pd.DataFrame(te_ary, columns=te.columns_)frequent_itemsets = fpgrowth(df, min_support=0.7, use_colnames=True)# 最小支持度为0.7，DataFrame返回的是列名（商品名）print('频繁项集：')print(frequent_itemsets)  # 频繁项集# metric用于评估规则以confidence为指标：confidence(A->C) = support(A+C) / support(A), range: [0, 1]# 评估指标的最小阈值为min_threshold=0.7rules = association_rules(frequent_itemsets, metric="confidence", min_threshold=0.7)  # 关联规则print('关联规则：')print(rules)if __name__ == '__main__':main()

输出为：

频繁项集：support              itemsets
0      1.0        (Kidney Beans)
1      0.8                (Eggs)
2      0.8  (Eggs, Kidney Beans)
关联规则：antecedents     consequents  antecedent support  consequent support  \换行
0          (Eggs)  (Kidney Beans)                 0.8                 1.0   
1  (Kidney Beans)          (Eggs)                 1.0                 0.8   support  confidence  lift  leverage  conviction  
0      0.8         1.0   1.0       0.0         inf  
1      0.8         0.8   1.0       0.0         1.0  

总结

1.Apriori算法

• 可能产生大量的候选集,以及可能需要重复扫描数据库，是Apriori算法的两大缺点。
• 主要改进方向：减少候选集产生、降低无效的扫描库次数、提高候选集与原数据的比较效率。

2.FP-growth算法

FP-growth算法是一种用于发现数据集中频繁模式的有效方法。FP-growth算法利用Apriori原则，执行更快。Apriori算法产生候选项集，然后扫描数据集来检查它们是否频繁。由于只对数据集扫描两次，因此FP-growth算法执行更快。在FP-growth算法中，数据集存储在一个称为FP树的结构中。FP树构建完成后，可以通过查找元素项的条件基及构建条件FP树来发现频繁项集。该过程不断以更多元素作为条件重复进行，直到FP树只包含一个元素为止。

优缺点：

优点：一般要快于Apriori。
缺点：实现比较困难，在某些数据集上性能会下降。适用数据类型：离散型数据。