本文主要是介绍Part-Ⅰ3. 稳态等效电路建模/损耗/效率(一),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
3.1 直流变压器模型
- 如下图所示,任何开关变换器都包含三个部分:电源输入端、输出端和控制输入端。输入功率按控制输入进行特定的功率变换输出到负载。理想状态下,这个过程以100%的效率完成。即 P i n = P o u t P_{in}=P_{out} Pin=Pout V g I g = V I V_gI_{g}=VI VgIg=VI
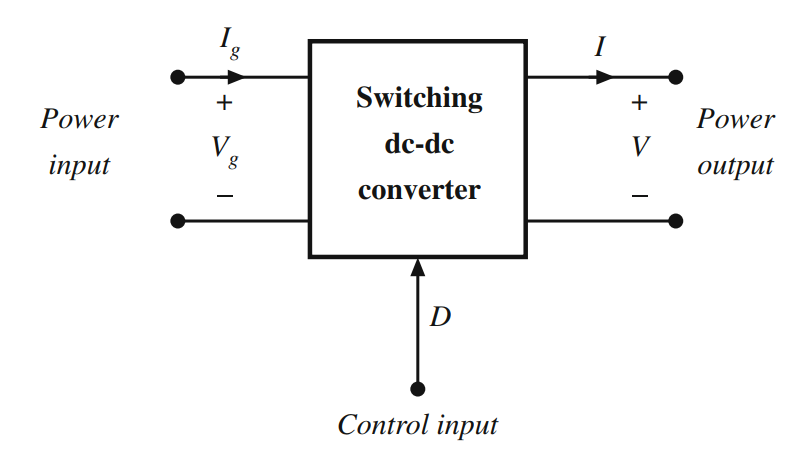
- 这种关系只有在平衡(DC)条件下成立,在瞬态过程,变换器的电感和电容存储的能量会改变。
- 在之前的内容中,可以得到变换器的输入输出电压表达式: V = M ( D ) V g V=M(D)V_g V=M(D)Vg M(D)为电压变换比,如Buck变换器的 M ( D ) = D M(D)=D M(D)=D,Boost变换器的 M ( D ) = 1 ( 1 − D ) M(D)=\frac{1}{(1-D)} M(D)=(1−D)1
- 通常情况下,对于工作在连续导通模式下,且包含相等数量的独立电感和电容的理想PWM变换器,可以证明变换比M(D)是D的函数,与负载无关。
- 根据以上表达式,可得 I g = M ( D ) I I_g=M(D)I Ig=M(D)I
- 现在我们有了输入输出电压关系、输入输出电流关系,可以获得一个等效的电路模型,输入功率与输出功率相同。输出电压等于匝数乘以输入电压,其中的匝数为平衡变换比 M ( D ) M(D) M(D)。
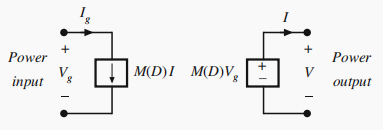
- 因此,可以使用如下图所示的理想变压器模型对理想的DC-DC变换器建模。这个模型表示了任何开关DC-DC变换器的一阶直流特性:理想情况下以占空比 D D D控制的100%效率的直流电压和电流的变换。水平的实线表示该元件是理想的,且能传递直流电压和电流。这种等效电路的优点:对于固定的占空比,它是时不变的,没有开关或开关纹波需要处理,且仅对波形重要的直流分量进行建模。
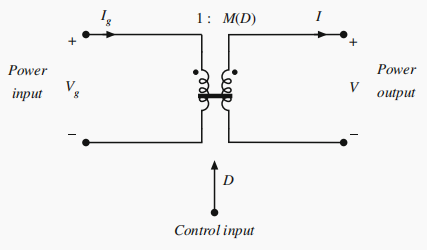
- 对于如下电路,进行戴维南等效电路之后,进行分析,输出电压 V V V为两个电阻分压得到。
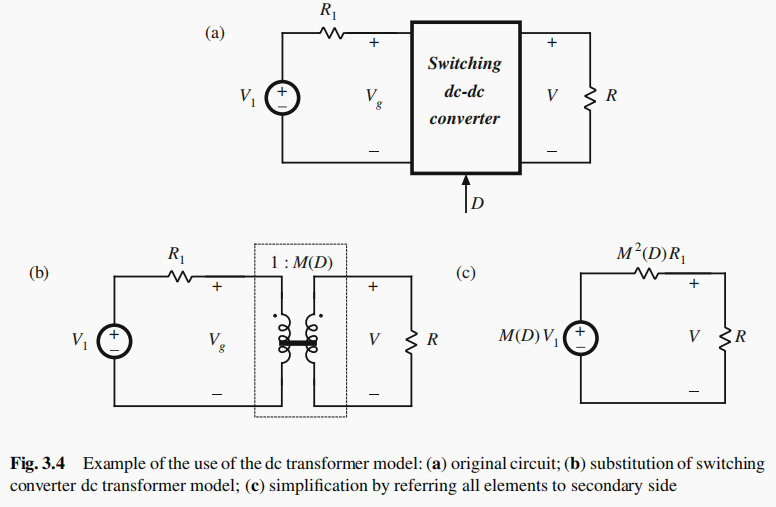
- 可得到 V = M ( D ) V 1 R M 2 ( D ) R 1 + R V=M(D)V_1\frac{R}{M^2(D)R_1+R} V=M(D)V1M2(D)R1+RR
- 显然,直流变压器等效电路的方法是理解变换器电路的有效工具。
考虑电感铜损
-
由前可得的直流变压器模型,来对变换器的其他属性进行建模。 添加电阻模拟功率损耗等非理想因素。
-
首先考虑下boost电路中的电感的铜损,实际电感器会表现出两种功率损耗:
- 由导线电阻导致的铜损;
- 由磁芯中的磁滞和涡流导致的磁芯损耗。
-
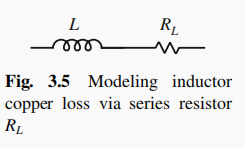
如下图,给出使用电感器 L L L与电阻 R L R_L RL 串联的结构描述适合电感器铜损的模型。
-
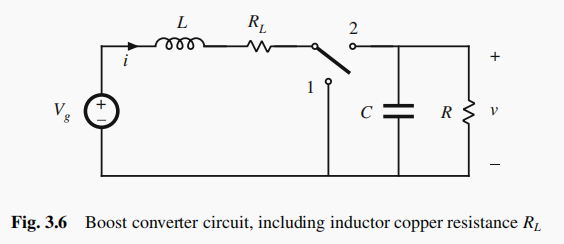
将此模型插入boost变换器中,使用电感伏秒平衡、电容电荷平衡和小纹波近似等原理分析电路
-
当 0 < t < D T s 0<t<DT_s 0<t<DTs,开关位于1位置
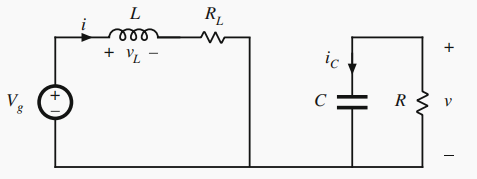
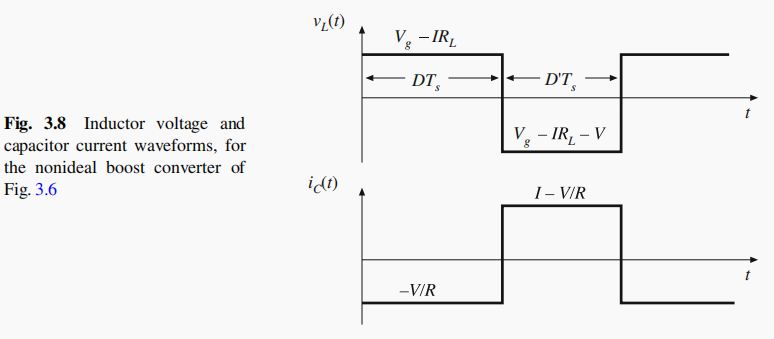
- 理想电感 L L L两端的电感电压为 v L ( t ) = V g − i ( t ) R L ≈ V g − I R L v_L(t)=V_g-i(t)R_L \approx V_g-IR_L vL(t)=Vg−i(t)RL≈Vg−IRL
- 电容 C C C的电流为 i C ( t ) = − v R ≈ − V R i_C(t)=-\frac{v}{R} \approx -\frac{V}{R} iC(t)=−Rv≈−RV
-
当 D T s < t < D ′ T s DT_s<t<D'T_s DTs<t<D′Ts,开关位于2位置
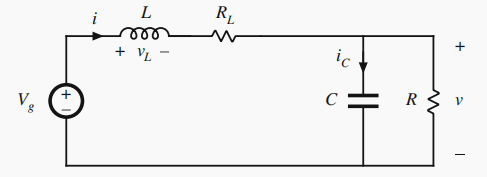
- 此时,电感 L L L两端的电感电压为 v L ( t ) = V g − i ( t ) R L − v ≈ V g − I R L − V v_L(t)=V_g-i(t)R_L-v \approx V_g-IR_L-V vL(t)=Vg−i(t)RL−v≈Vg−IRL−V
- 电容 C C C的电流为 i C ( t ) = i ( t ) − v R ≈ I − V R i_C(t)=i(t)-\frac{v}{R} \approx I-\frac{V}{R} iC(t)=i(t)−Rv≈I−RV
-
电感伏秒平衡得 ( V g − I R L ) D + ( V g − I R L − V ) D ′ = 0 (V_g-IR_L)D+(V_g-IR_L-V)D'=0 (Vg−IRL)D+(Vg−IRL−V)D′=0
-
电容电荷平衡得 ( − V R ) D + ( I − V R ) D ′ = 0 (-\frac{V}{R})D+(I-\frac{V}{R})D'=0 (−RV)D+(I−RV)D′=0
-
联立两个关系式,可解得 I = V R D ′ I=\frac{V}{RD'} I=RD′V V = 1 D ′ V g ( 1 + R L R D ′ 2 ) V=\frac{1}{D'}\frac{V_g}{(1+\frac{R_L}{RD'^2})} V=D′1(1+RD′2RL)Vg
-
波形图如下
-
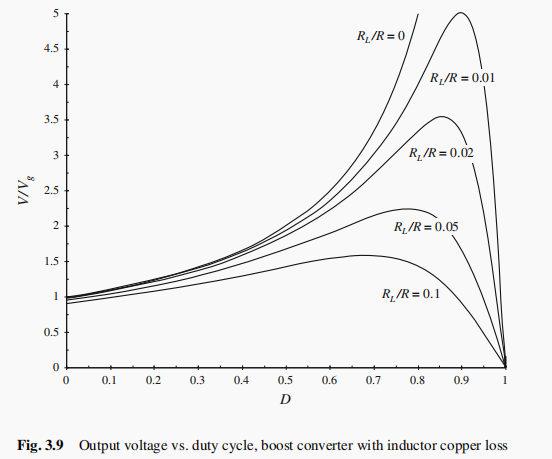
以上便是变换器输出电压的求解方法,下面给出了不同 R L / R R_L/R RL/R情况下的图形。从表达式中不难发现,包含了两个部分:
- 1 / D ′ 1/D' 1/D′,这是 R L = 0 R_L=0 RL=0时的理想变换比。
- 1 / ( 1 + R L / R D ′ 2 ) 1/(1+R_L/RD'^2) 1/(1+RL/RD′2),这个描述了电感绕线电阻的影响。如果 R L R_L RL远小于 R D ′ 2 RD'^2 RD′2,第二项近似为0,变换比近似等于理想值。随着 R L R_L RL的相较于 R D ′ 2 RD'^2 RD′2的逐渐增加,第二项的值不能忽略了,此时的变换比就减小了。
-
上图还有一个作用,就是可以看出电感绕线电阻限制了变换器的最大输出电压。
- 如 R L / R = 0.02 R_L/R=0.02 RL/R=0.02时,可以看出 V / V g V/V_g V/Vg的最大值接近3.5。
- 如期望 V / V g V/V_g V/Vg取到5,则电感绕线电阻必须减小到小于负载电阻的1%。问题是,减小电感绕线电阻需要构建更大,更重,更贵的电感器。
-
因此,通常是先正确建模考虑铜损等问题,选择能够满足设计需求的最小电感器来优化电路设计。接下来说明如何考虑铜损因素建模。
这篇关于Part-Ⅰ3. 稳态等效电路建模/损耗/效率(一)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








