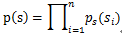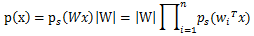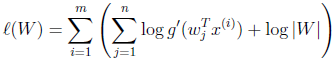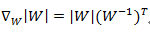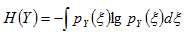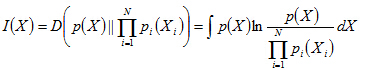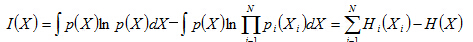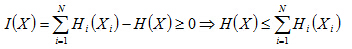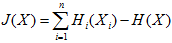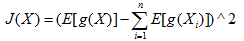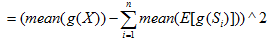本文主要是介绍独立成分分析ICA系列4:ICA的最优估计方法综述,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
ICA算法的研究可分为基于信息论准则的迭代估计方法和基于统计学的代数方法两大类,从原理上来说,它们都是利用了源信号的独立性和非高斯性。基于信息论的方法研究中,各国学者从最大熵、最小互信息、最大似然和负熵最大化等角度提出了一系列估计算法。如FastICA算法, Infomax算法,最大似然估计算法等。基于统计学的方法主要有二阶累积量、四阶累积量等高阶累积量方法。
1.最大似然估计算法
1.1 目标函数部分
假设信号Si有概率密度函数Ps(t),由于我们假定信号源是相互独立的,其实经过白化处理后就变成独立的了;那么在给定时刻的联合分布函数为:
知道了信号源的联合分布Ps(t),再由分解矩阵S=WX,可以得出信号x的联合分布函数。
其中|W|为W的行列式。
由于没有先验知识,只知道原信号之间特征独立,且最多有一个是高斯分布,所以没有办法确定Ps(t)的分布,所以我们选取一个概率密度函数Ps'(t)来近似估计Ps(t)。
概率密度函数由累积分布函数F(x)求导得到。
F(x)要满足两个性质:1单调递增;2值域在[0 1]范围
我们发现sigmoid函数的定义域是负无穷到正无穷,值域为0到1,缓慢递增的性质。基于sigmoid函数良好的性质,我们用sigmoid函数来近似估计F(x),通过求导得到Ps'(t)。
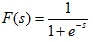
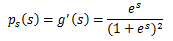
两函数图像如图:
如果我们预先知道Ps(t)的分布函数,那就不用假设了;但是在缺失的情况下,sigmoid函数大多数情况下能够起到不错的效果。由于Ps(t)是个对称函数,所以均值E[s]=0,那么E[x]=E[AS]=0,x的均值也是0。
知道了Ps(t),就剩下W了,在给定训练样本{Xi(Xi1,Xi2,........Xin),i=1,2....m个样本,样本的对数似然估计如下:
(W=H')
T=m为独立同分布观测数据的样本数。最大化此似然函数就可获得关于参数W 的最佳估计。
1.2 优化部分(梯度下降算法)
接下来就是对W求导了,这里牵涉一个问题是对行列式|W|进行求导的方法,属于矩阵微积分
最终得到的求导后公式如下,logg'(s)的导数为1-2g(s):
2.负熵最大的FastICA算法
2.1目标函数部分
2.1.1负熵判别准则
由极大熵原理可知,在方差相同的条件下,所有概率分布中,高斯分布的熵最大;因而我们可以利用熵来度量分布的非高斯性。因此通过度量分离结果的非高斯性,作为分离结果独立性的度量;当非高斯性达到最大时,表明已完成对各个分量的分离。因为FastICA算法以负熵最大作为一个搜寻方向,因此先讨论一下负熵判决准则。由信息论理论可知:在所有等方差的随机变量中,高斯变量的熵最大,因而我们可以利用熵来度量非高斯性,常用熵的修正形式,即负熵。
负熵的定义:
其中XG是和X具有相同协方差的随机变量,H()为变量的微分熵
微分熵定义:
联系极大熵原理,XG为高斯分布,所以J(X)>=0;当且仅当X本身也为高斯分布时=0;所以J(x)的值越大,证明X的非高斯性越强,
2.1.2负熵与独立性关系
假设n维随机变量X=[X1,X2……Xn],其互信息为I(X):
互信息即为:独立分布乘积分布与联合分布之间的负熵J(X),当Xi相互独立时,互信息为0;
由于计算J(X)需要联合分布函数和各个分量的分布函数,这个显然不切实际;所以采用非线性变换g(x)后的均值期望来近似替代。
由于Xi即为观测数据X分离后的独立变量Si,再由中心极限定理可知,若随机变量X有许多相互独立的随机变量信号源Si相互组合而成,则不论Si为何种分布,观测变量数据X比Si具有更强的高斯性,换言之Xi的非高斯性更强。所以,负熵J(X)的值越小,即此时的互信息I(X)越小,此时分离的变量Si独立性越好。
2.2 优化部分
快速ICA算法是找一个方向以便WX具有最大的非高斯性,也即最大的相互独立性;这里的独立性通过负熵来给出,通过均值近似估计来计算。这里通过白化处理,使W的范数为1,即使WX的方差估计为1;
优化过程推导比较复杂,公式太多!
实践中,FastICA算法中用的期望必须用它们的估计值代替。当然最好的估计是相应的样本平均。理想情况下,所有的有效数据都应该参与计算,但这会降低计算速度。所以通常用一部分样本的平均来估计,样本数目的多少对最后估计的精确度有很大影响。迭代中的样本点应该分别选取,假如收敛不理想的话,可以增加样本的数量。
这篇关于独立成分分析ICA系列4:ICA的最优估计方法综述的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!