本文主要是介绍【端到端可微1】端到端的训练,使用反向传播,要求过程可微分,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
文章目录
- 背景
- 想法: Weighted least-squares fitting
- 方法: Backpropagating through the fitting procedure.
- 温习之前的基础
- 前向传播
- 反向传播
- 总结
背景
想做一个端到端训练的模型,将最小二乘嵌入其中。因此有了这系列文章。
想法: Weighted least-squares fitting
我们想把“最小二乘模块”嵌入深度学习中,将其作为一份子参与端到端的训练
我们设计了加权最小二乘问题。设W∈Rm×m是包含每个观测的权值wi的对角矩阵。在我们的框架中,观测结果将对应于图像参考框架中的固定(x, y)坐标,权重将由基于图像的深度网络生成。加权最小二乘问题是

方法: Backpropagating through the fitting procedure.
我们深度学习最后的卷积输出特征图,我们定义这个特征图为“一个加权像素坐标列表(xi, yi, wi)”。其中坐标(xi, yi)是固定的,而加权wi是由一个基于输入图像的深层网络生成的。我们可以利用这些值构造矩阵X, Y和w,求解加权最小二乘问题,通过加权像素坐标得到最佳拟合曲线的参数β。
与其将拟合过程作为一个单独的后处理步骤,我们可以反向传播它,并在兴趣β参数上应用一个损失函数,而不是间接地在网络产生的权值映射上。通过这种方式,我们获得了一个强大的工具,可以在深度学习框架中以端到端方式解决最小二乘的问题。
注意,方程3只涉及可微矩阵运算。因此,可以计算β对W的导数,从而也可以计算深度网络的参数。通过矩阵变换反向传播的细节已经很好地理解了。我们使用Cholesky分解推导这个问题的梯度。
β对W的导数表示为dβ/dW。这里的β和W都是变量,dβ/dW表示β对W的变化率。在求解这个导数时,我们需要将β作为独立变量,W作为因变量,然后对W进行求导。
具体的求导方法取决于β和W的具体形式和关系。如果β和W都是标量变量,那么可以直接对W求导得到dβ/dW。如果β和W是向量或矩阵变量,那么我们需要对每个元素或矩阵元素分别求导,得到一个与W相同形状的导数矩阵。
需要注意的是,在求解dβ/dW时,我们通常将其他变量视为常数,即假设它们不随W的变化而变化。这是因为我们只关注β对W的导数,而不考虑其他变量对此导数的影响。
总之,β对W的导数表示为dβ/dW,具体的求导方法取决于β和W的形式和关系。
温习之前的基础
1、2月10日 感知器+浅层神经网络+反向传播+tensorflow
2、链式法则,论文:Introduction to Gradient Descent and Backpropagation Algorithm

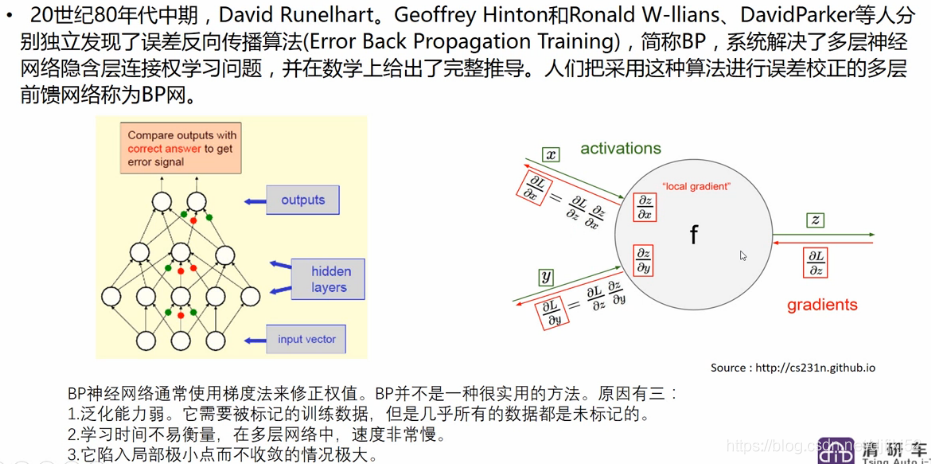
BP 算法是一种参数学习方法,一般分为两个过程:前向传播(求误差),反向传播(误差回传)。
那么什么是前向传播、反向传播呢?这里先说结论:前向传播是为反向传播准备好要用到的数值,反向传播本质上是一种求梯度的高效方法。
求梯度是为了什么呢?就是为了更新模型的参数(权重 W 和偏置 b)。
所有参数值随机初始化(论文乱写一通),前向传播(提交论文),误差函数(审稿),反向传播(审稿人:你这不行,改!),参数更新(修改论文),前向传播,…;反反复复,论文发表(模型训练完毕)。
前向传播
在正式介绍前向传播前,先简单介绍计算图(Computational Graph)的概念, f ( x , y , z ) = ( x + y ) ∗ z 的计算图
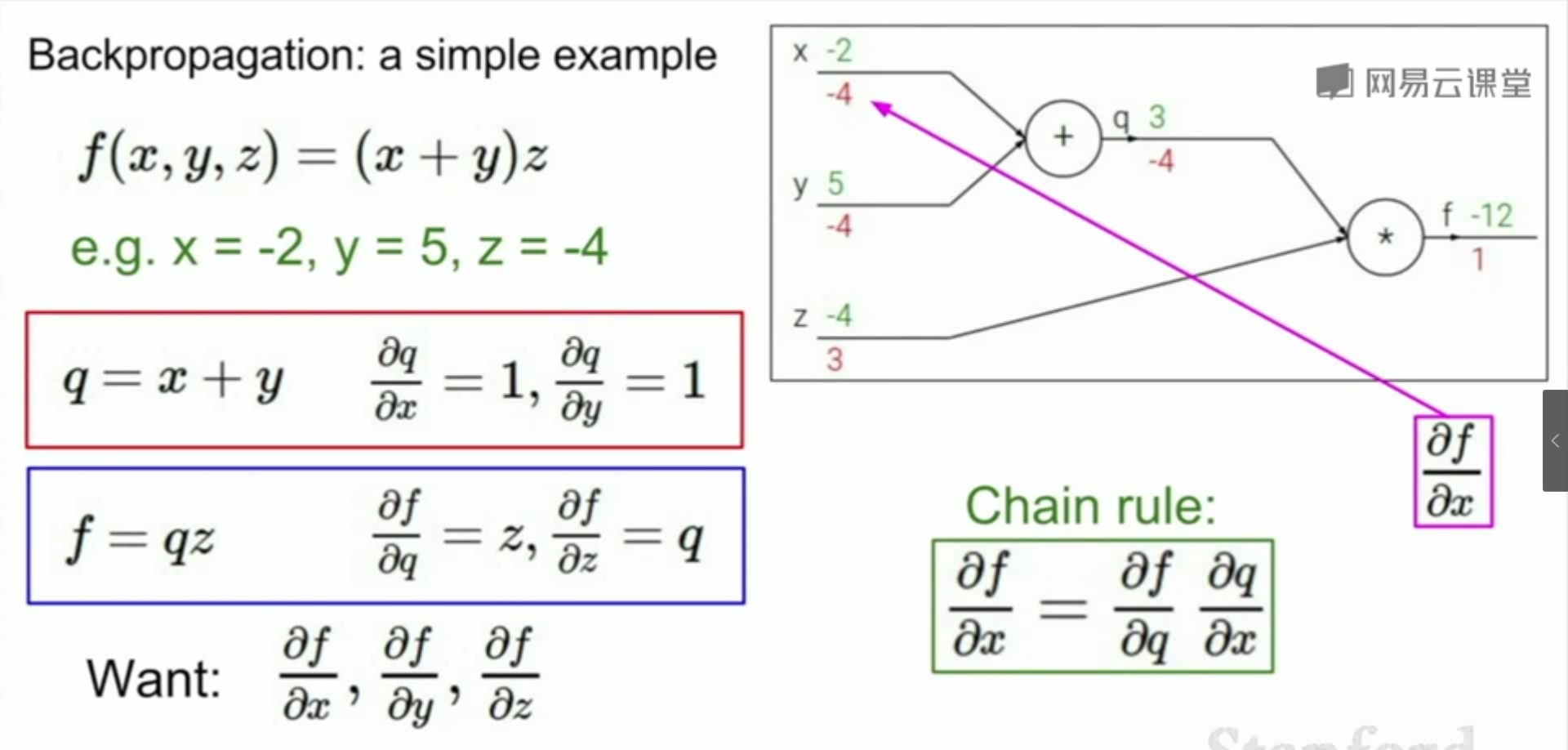
分别赋值 x = − 2 , y = 5 , z = − 4 ,从计算图的左边开始,数据开始流动,依次计算出 q 、 f 。
最终得到计算图中那 6 个绿色的数字,这就是前向传播的结果。
反向传播
我们说了,反向传播本质上是一种求梯度的高效方法。
总结
这系列文章将逐步完成一个端到端可微的模型,挖个坑。
项目开启时间:2023-07-04
但是一直拖到了11月30,最近同事讨论问题才想起来继续实施。
这篇关于【端到端可微1】端到端的训练,使用反向传播,要求过程可微分的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




