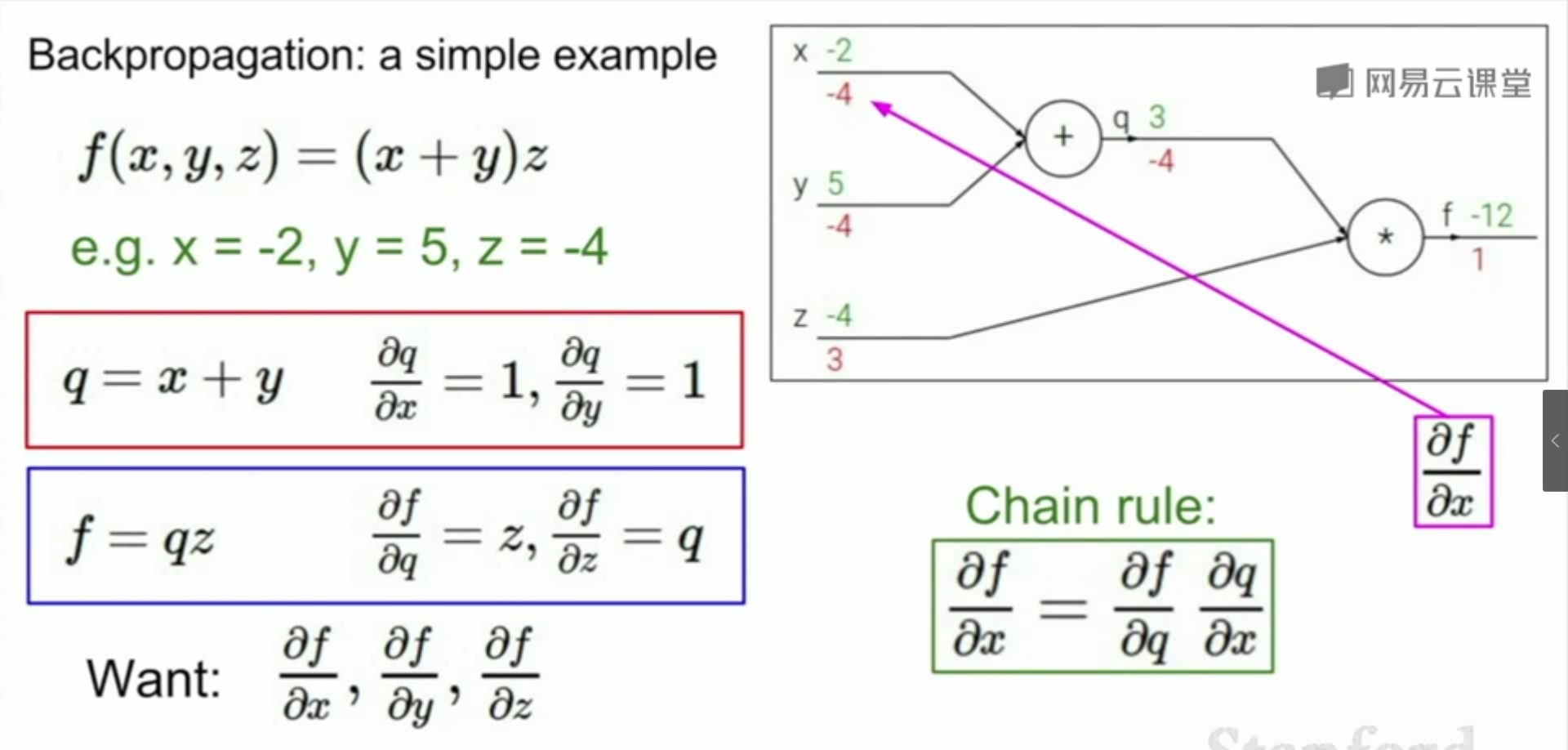
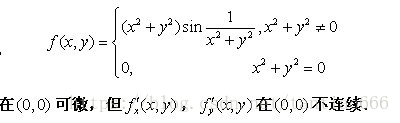可微专题
深度学习中的可微编程:从微分方程到物理模拟
引言 可微编程(Differentiable Programming)是深度学习领域的一个新兴概念,旨在将传统编程中的数学模型(如微分方程)与深度学习模型结合,构建出更加灵活、可解释的模型。这一技术为物理模拟、科学计算等领域带来了新的可能性,使得深度学习不仅能够进行预测,还能融入复杂的物理规律进行精确模拟。本篇博文将探讨可微编程的基本原理、常见应用场景,特别是在物理模拟中的实践,以及未来的发展方
52.1 %AP!AutoAssign:Anchor-free最强检测网络!密集目标检测的可微标签分配
点击关注上方“AI公园”,并“星标”公号 技术硬文,第一时间送达! AI公园 AutoAssign:以52.1%的AP成就最强Anchor-free目标检测网络!用于密集目标检测的可微标签分配,模型表现SOTA!优于所有现有的一级检测器,如ATSS、FreeAnchor和FCOS等网络,注:并没有成功收录到ECCV 2020。 作者团队:旷视研究院 1 摘要 在本文中,我们提出了一种具有完全d
漫步数学分析三十三——可微的条件
因为雅克比矩阵给出了有效的计算方法,因此我们知道通常的偏导存在就意味着导数 Df Df存在。不幸的是这结论在一般情况下是不成立的,例如将 f:R2→R f:R^2\to R 定义为 y=0,f(x,y)=x;x=0,f(x,y)=y; y=0,f(x,y)=x;x=0,f(x,y)=y;其余情况下 f(x,y)=1 f(x,y)=1,那么 ∂f/∂x,∂f/∂y \partial f/\parti
数学分析复习: 连续函数、可微函数的重要结论梳理
文章目录 连续函数、可微函数的重要结论梳理总结细节1.有界性定理2.最值定理3.介值定理4.中值定理5.洛必达法则6.泰勒公式 本篇文章适合个人复习翻阅,不建议新手入门使用 连续函数、可微函数的重要结论梳理 总结 在数学分析一中,关于闭区间上的连续函数,我们用区间套公理可获得一系列结论 区间套定理 ⇒ \Rightarrow ⇒ 有界性定理 ⇒ \Righta
高等数学的函数连续,可导,可微和偏导数连续的关系(多元)
结论(一元函数范畴内) 可导与连续的关系:可导必连续,连续不一定可导; 可微与连续的关系:可微与可导是一样的; 可积与连续的关系:可积不一定连续,连续必定可积; 可导与可积的关系:可导一般可积,可积推不出一定可导; 这个就不多说了。。。 下面是多元函数的关系 先上图 很显然函数连续,可导,可微和偏导数连续的关系可以从图中看出 函数连续不一定的函数可微(例子:y=|x|
【端到端可微1】端到端的训练,使用反向传播,要求过程可微分
文章目录 背景想法: Weighted least-squares fitting方法: Backpropagating through the fitting procedure.温习之前的基础前向传播反向传播 总结 背景 想做一个端到端训练的模型,将最小二乘嵌入其中。因此有了这系列文章。 想法: Weighted least-squares fitting 我们想把“最小
NIPS 2022 Poster | DCD-FG:大规模因子图的可微因果发现
文章目录 一、论文关键信息二、基础概念三、主要内容1. Motivations2. Insights3. 解决方案的关键 四、总结 CSDN 叶庭云:https://yetingyun.blog.csdn.net/ 一、论文关键信息 论文标题:Large-Scale Differentiable Causal Discovery of Factor Graphs 会议