本文主要是介绍趣题:构造多边形使得过边界上某一点的任意直线均能等分面积,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
这是 2008 年莫斯科数学竞赛中的一个问题。构造一个多边形,使得这个多边形的边界上存在这样的一个点 O :经过点 O 的任意直线均会把该多边形分成面积相等的两份。这看起来不大可能对吧?但其实构造却并不困难。你能想出来吗?
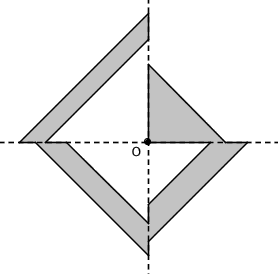
首先,在平面直角坐标系的第一象限内,沿着坐标轴放置一个等腰直角三角形。在第二象限内,拼接一个面积相等的等腰梯形。在第三象限和第四象限内,继续摆放面积相等的等腰梯形,并且让它们离原点越来越远,以保证最终所得的图形确实是一个多边形(而不是一块环形区域)。现在,把平面直角坐标系的原点记作点 O ,则过点 O 的任意一条直线都将把整个多边形分成面积相等的两份。
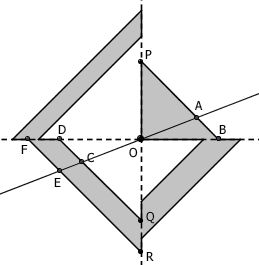
为了验证这一点,我们举一个例子。如上图,过点 O 作一条过一三象限的直线。容易看出,三角形 OAB 的面积占了三角形 OPB 面积的几分之几,三角形 OCD 的面积就占了三角形 OQD 面积的几分之几,同样地三角形 OEF 的面积就占了三角形 ORF 面积的几分之几,从而梯形 CDFE 的面积就是梯形 QDFR 的几分之几。由于三角形 OPB 的面积等于梯形 QDFR 的面积,因此三角形 OAB 的面积也就总是等于梯形 CDFE 的面积。自然,三角形 OAP 的面积也等于梯形 QCER 的面积了。而第二象限和第四象限的图形面积也是相等的,因此这条直线两侧的面积相等。过点 O 作其他方向上的直线,两侧的面积也相等,道理也一样。
这篇关于趣题:构造多边形使得过边界上某一点的任意直线均能等分面积的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!


