本文主要是介绍CMSIS-DSP实数FFT相关API(单精度浮点float),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目录
1. CMSIS-DSP的实数FFT
2. 频域上求模值
3. 如何求解相位
4. 对比python的求解过程
5. 在频域上以模和相角的方式还原信号
6. 求能量值
平台:STM32F407-Discovery+CMSIS-DSP-V1.6.0
1. CMSIS-DSP的实数FFT
文件:\CMSIS\DSP\Source\TransformFunctions\arm_rfft_fast_f32.c
| 函数原型 | void arm_rfft_fast_f32( arm_rfft_fast_instance_f32 * S, float32_t * p, float32_t * pOut, uint8_t ifftFlag) |
| 函数功能 | 实数FFT的实现(浮点数) |
| 参数 | S:指针,指向实例arm_rfft_fast_instance_f32 structure. p: 输入buffer(实序列). pOut: 输出buffer. IfftFlag:RFFT-0,RIFFT-1 |
| 返回值 | Void |
| 定义处(源文件) | |
| 声明处(头文件) |
一般来说,实序列FFT转换到频域上后,就是复数序列,且具有对称性质,其中实部偶对称,虚部奇对称。比如64个点的时序列FFT后,得到的复数序列如下:注意直流分量和正频率分量所在的位置,这两个特殊的分量虚数部分都是0,下面的结果是用numpy的fft模块运行得到:
[
2016. +0.j //直流分量
-32. +651.374964j
-32. +324.9014524j
-32. +215.72647697j
-32. +160.87486375j
-32. +127.75116108j
-32. +105.48986269j
-32. +89.43400872j
-32. +77.254834j
-32. +67.65831544j
-32. +59.86778918j
-32. +53.38877458j
-32. +47.89138441j
-32. +43.14700523j
-32. +38.99211282j
-32. +35.30655922j
-32. +32.j
-32. +29.00310941j
-32. +26.26172131j
-32. +23.73281748j
-32. +21.38171641j
-32. +19.18006188j
-32. +17.10435635j
-32. +15.13487283j
-32. +13.254834j
-32. +11.44978308j
-32. +9.70709388j
-32. +8.01558273j
-32. +6.36519576j
-32. +4.7467516j
-32. +3.15172491j
-32. +1.57205919j //实部相同,虚部互反
-32. +0.j //正频率分量(奈奎斯特频率分量)
-32. -1.57205919j //实部相同,虚部互反
-32. -3.15172491j
-32. -4.7467516j
-32. -6.36519576j
-32. -8.01558273j
-32. -9.70709388j
-32. -11.44978308j
-32. -13.254834j
-32. -15.13487283j
-32. -17.10435635j
-32. -19.18006188j
-32. -21.38171641j
-32. -23.73281748j
-32. -26.26172131j
-32. -29.00310941j
-32. -32.j
-32. -35.30655922j
-32. -38.99211282j
-32. -43.14700523j
-32. -47.89138441j
-32. -53.38877458j
-32. -59.86778918j
-32. -67.65831544j
-32. -77.254834j
-32. -89.43400872j
-32. -105.48986269j
-32. -127.75116108j
-32. -160.87486375j
-32. -215.72647697j
-32. -324.9014524j
-32. -651.374964j
]
arm_rfft_fast_f32(,, out_buff, )的输出也具有类似的特点,同样是64个点的FFT,一样的输入,测试代码如下:
#define RFFT_LEN 64static float32_t Input_f32[RFFT_LEN];
static float32_t Input_f32_bak[RFFT_LEN];
static float32_t Output_f32[RFFT_LEN];void rfft_f32_test(void)
{uint16_t i;arm_rfft_fast_instance_f32 S;/* 初始化结构体S中的参数 */arm_rfft_fast_init_f32(&S, RFFT_LEN);for(i=0; i<RFFT_LEN; i++){Input_f32[i] = i;Input_f32_bak[i] = Input_f32[i];}arm_rfft_fast_f32(&S, Input_f32, Output_f32, 0);for(i=0; i<RFFT_LEN; i++){printf("[%d], %f\r\n", i, Output_f32[i]);}}
输出:out_buff
[0], 2016.000000 //第一个点的实部和虚部
[1], -32.000000[2], -32.000015 //第二个点的实部和虚部
[3], 651.374939[4], -31.999990
[5], 324.901428[6], -32.000008
[7], 215.726471
[8], -31.999998
[9], 160.874878
[10], -32.000000
[11], 127.751160
[12], -32.000004
[13], 105.489853
[14], -32.000015
[15], 89.433998
[16], -32.000000
[17], 77.254837
[18], -31.999998
[19], 67.658318
[20], -32.000004
[21], 59.867783
[22], -32.000000
[23], 53.388767
[24], -32.000000
[25], 47.891380
[26], -32.000004
[27], 43.147003
[28], -32.000008
[29], 38.992107
[30], -32.000008
[31], 35.306553
[32], -32.000000
[33], 32.000000
[34], -32.000008
[35], 29.003107
[36], -31.999992
[37], 26.261724
[38], -31.999996
[39], 23.732821
[40], -32.000000
[41], 21.381718
[42], -32.000000
[43], 19.180065
[44], -32.000008
[45], 17.104353
[46], -32.000000
[47], 15.134871
[48], -32.000000
[49], 13.254833
[50], -31.999996
[51], 11.449793
[52], -31.999994
[53], 9.707090
[54], -31.999989
[55], 8.015587
[56], -32.000004
[57], 6.365196
[58], -32.000008
[59], 4.746758
[60], -32.000011
[61], 3.151733
[62], -31.999983
[63], 1.572052 //最后是下标为31的点的信息,相当于只输出前31个复数点的信息
//64个实数点对应应该是64个复数点信息,但是有一半数据是对称的。
2. 频域上求模值
上面讲了对arm_rfft_fast_f32()的输出是顺序输出,得到实际的每个点的复数值,每个点有实部和虚部后就可以进行求模以及求解相位等计算。但是,如果逐个点进行计算的话,在计算量和存储上都会有浪费,CMSIS-DSP库里就有现成的API可用,这些API都极大地进行了优化。
文件:CMSIS\DSP\Source\ComplexMathFunctions\arm_cmplx_mag_f32.c
| 函数原型 | void arm_cmplx_mag_f32( float32_t * pSrc, float32_t * pDst, uint32_t numSamples) |
| 函数功能 | 求解复数序列的模值 |
| 参数 | pSrc:输入的复数序列,注意排序!(实部+虚部) pDst: 输出的buffer(实序列). numSamples: 输入的复数序列的长度 |
| 返回值 | Void |
| 定义处(源文件) | |
| 声明处(头文件) |
测试:
#define RFFT_LEN 64static float32_t Input_f32[RFFT_LEN];
static float32_t Input_f32_bak[RFFT_LEN];
static float32_t Output_f32[RFFT_LEN];
static float32_t mag_f32[RFFT_LEN];void rfft_f32_test(void)
{uint16_t i;arm_rfft_fast_instance_f32 S;/* 初始化结构体S中的参数 */arm_rfft_fast_init_f32(&S, RFFT_LEN);for(i=0; i<RFFT_LEN; i++){Input_f32[i] = i;Input_f32_bak[i] = Input_f32[i];}arm_rfft_fast_f32(&S, Input_f32, Output_f32, 0);for(i=0; i<RFFT_LEN; i++){printf("[%d], %f\r\n", i, Output_f32[i]);}printf("=====================================\r\n");arm_cmplx_mag_f32(Output_f32, mag_f32, RFFT_LEN);for(i=0; i<RFFT_LEN; i++){printf("[%d], %f\r\n", i, mag_f32[i]);}
}
结果:
[17:15:17.081] 0, 2016.253906 //直流分量
[17:15:17.097] 1, 652.160522
[17:15:17.113] 2, 326.473480
[17:15:17.129] 3, 218.086929
[17:15:17.145] 4, 164.026596
[17:15:17.161] 5, 131.697983
[17:15:17.177] 6, 110.236603
[17:15:17.193] 7, 94.986534
[17:15:17.209] 8, 83.620033
[17:15:17.225] 9, 74.844154
[17:15:17.241] 10, 67.883369
[17:15:17.257] 11, 62.244362
[17:15:17.272] 12, 57.598473
[17:15:17.288] 13, 53.718376
[17:15:17.305] 14, 50.441895
[17:15:17.321] 15, 47.650322
[17:15:17.337] 16, 45.254833
[17:15:17.353] 17, 43.187737
[17:15:17.369] 18, 41.396591
[17:15:17.385] 19, 39.840263
[17:15:17.400] 20, 38.486073
[17:15:17.417] 21, 37.307838
[17:15:17.432] 22, 36.284424
[17:15:17.448] 23, 35.398647
[17:15:17.464] 24, 34.636551
[17:15:17.480] 25, 33.986725
[17:15:17.496] 26, 33.439907
[17:15:17.512] 27, 32.988617
[17:15:17.528] 28, 32.626923
[17:15:17.545] 29, 32.350151
[17:15:17.561] 30, 32.154846
[17:15:17.577] 31, 32.038574
[17:15:17.577] 32, 0.000000 //这里的值,对应的是N/2处的值
[17:15:17.593] 33, 0.000000 //后面的值,偶对称
[17:15:17.609] 34, 0.000000
[17:15:17.625] 35, 0.000000
[17:15:17.640] 36, 0.000000
[17:15:17.656] 37, 0.000000
[17:15:17.672] 38, 0.000000
[17:15:17.688] 39, 0.000000
[17:15:17.704] 40, 0.000000
[17:15:17.720] 41, 0.000000
[17:15:17.736] 42, 0.000000
[17:15:17.752] 43, 0.000000
[17:15:17.752] 44, 0.000000
[17:15:17.768] 45, 0.000000
[17:15:17.784] 46, 0.000000
[17:15:17.800] 47, 0.000000
[17:15:17.816] 48, 0.000000
[17:15:17.832] 49, 0.000000
[17:15:17.848] 50, 0.000000
[17:15:17.865] 51, 0.000000
[17:15:17.881] 52, 0.000000
[17:15:17.897] 53, 0.000000
[17:15:17.912] 54, 0.000000
[17:15:17.912] 55, 0.000000
[17:15:17.928] 56, 0.000000
[17:15:17.944] 57, 0.000000
[17:15:17.960] 58, 0.000000
[17:15:17.976] 59, 0.000000
[17:15:17.992] 60, 0.000000
[17:15:18.008] 61, 0.000000
[17:15:18.024] 62, 0.000000
[17:15:18.040] 63, 0.000000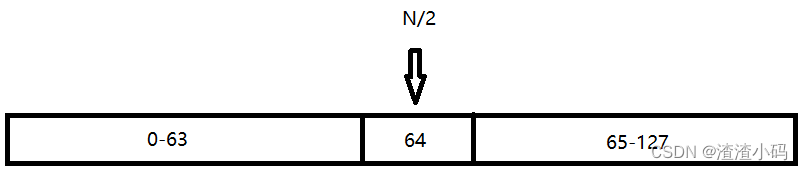
从上面两个实验来看,FFT结果以及求模,都只会输出前一半的数据,且都是顺序交替输出。
3. 如何求解相位
相位的求解没有可用的API,只能根据定义去求解,求解出来的是弧度制:
phase=arctan(虚部/实部)
自己编写算法求解即可,完整测试代码:
#define RFFT_LEN 64static float32_t Input_f32[RFFT_LEN];
static float32_t Input_f32_bak[RFFT_LEN];
static float32_t Output_f32[RFFT_LEN];
static float32_t mag_f32[RFFT_LEN];
static float32_t phase_f32[RFFT_LEN];void cal_phase_f32(float32_t *in_buf, float32_t *phase, uint16_t _usFFTPoints)
{float32_t real, img;uint16_t i;for (i=0; i <_usFFTPoints; i++){real= in_buf[2*i]; /* 实部 */img= in_buf[2*i + 1]; /* 虚部 *//* atan2求解的结果范围是(-pi, pi], 弧度制 */phase[i] = atan2(img, real);}
}void rfft_f32_test(void)
{uint16_t i;arm_rfft_fast_instance_f32 S;/* 初始化结构体S中的参数 */arm_rfft_fast_init_f32(&S, RFFT_LEN);for(i=0; i<RFFT_LEN; i++){Input_f32[i] = i;Input_f32_bak[i] = Input_f32[i];}arm_rfft_fast_f32(&S, Input_f32, Output_f32, 0);for(i=0; i<RFFT_LEN; i++){printf("[%d], %f\r\n", i, Output_f32[i]);}arm_cmplx_mag_f32(Output_f32, mag_f32, RFFT_LEN);printf("=====================================\r\n");for(i=0; i<RFFT_LEN; i++){printf("[%d], %f\r\n", i, mag_f32[i]);}cal_phase_f32(Output_f32, phase_f32, RFFT_LEN);printf("=====================================\r\n");for(i=0; i<RFFT_LEN; i++){printf("[%d], %f\r\n", i, phase_f32[i]);}
}
输出的相位信息:
[17:15:18.104] 0, 0.000000 //直流分量
[17:15:18.104] 1, 1.619884
[17:15:18.120] 2, 1.668971
[17:15:18.136] 3, 1.718058
[17:15:18.152] 4, 1.767146
[17:15:18.167] 5, 1.816233
[17:15:18.183] 6, 1.865321
[17:15:18.183] 7, 1.914408
[17:15:18.200] 8, 1.963495
[17:15:18.216] 9, 2.012583
[17:15:18.232] 10, 2.061670
[17:15:18.248] 11, 2.110758
[17:15:18.264] 12, 2.159845
[17:15:18.280] 13, 2.208932
[17:15:18.295] 14, 2.258020
[17:15:18.311] 15, 2.307107
[17:15:18.311] 16, 2.356194
[17:15:18.328] 17, 2.405282
[17:15:18.344] 18, 2.454369
[17:15:18.360] 19, 2.503457
[17:15:18.376] 20, 2.552544
[17:15:18.392] 21, 2.601631
[17:15:18.408] 22, 2.650719
[17:15:18.424] 23, 2.699806
[17:15:18.440] 24, 2.748893
[17:15:18.456] 25, 2.797981
[17:15:18.471] 26, 2.847068
[17:15:18.487] 27, 2.896156
[17:15:18.487] 28, 2.945243
[17:15:18.503] 29, 2.994330
[17:15:18.519] 30, 3.043418
[17:15:18.535] 31, 3.092505
[17:15:18.551] 32, 0.000000 //N/2
[17:15:18.567] 33, 0.000000
[17:15:18.583] 34, 0.000000
[17:15:18.600] 35, 0.000000
[17:15:18.616] 36, 0.000000
[17:15:18.632] 37, 0.000000
[17:15:18.647] 38, 0.000000
[17:15:18.647] 39, 0.000000
[17:15:18.663] 40, 0.000000
[17:15:18.679] 41, 0.000000
[17:15:18.695] 42, 0.000000
[17:15:18.711] 43, 0.000000
[17:15:18.727] 44, 0.000000
[17:15:18.743] 45, 0.000000
[17:15:18.759] 46, 0.000000
[17:15:18.775] 47, 0.000000
[17:15:18.792] 48, 0.000000
[17:15:18.808] 49, 0.000000
[17:15:18.808] 50, 0.000000
[17:15:18.824] 51, 0.000000
[17:15:18.840] 52, 0.000000
[17:15:18.855] 53, 0.000000
[17:15:18.871] 54, 0.000000
[17:15:18.887] 55, 0.000000
[17:15:18.903] 56, 0.000000
[17:15:18.919] 57, 0.000000
[17:15:18.935] 58, 0.000000
[17:15:18.951] 59, 0.000000
[17:15:18.968] 60, 0.000000
[17:15:18.983] 61, 0.000000
[17:15:18.983] 62, 0.000000
[17:15:18.999] 63, 0.000000
4. 对比python的求解过程
测试代码:
import numpy as np
signal=[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63]
fftresult=np.fft.fft(signal)
print(fftresult)
magnitude=np.abs(fftresult)
print(magnitude)
phase=np.angle(fftresult)
print(phase)
FFT结果:
2016. +0.j
-32. +651.374964j //20.355467625
-32. +324.9014524j
-32. +215.72647697j
-32. +160.87486375j
-32. +127.75116108j
-32. +105.48986269j
-32. +89.43400872j
-32. +77.254834j
-32. +67.65831544j
-32. +59.86778918j
-32. +53.38877458j
-32. +47.89138441j
-32. +43.14700523j
-32. +38.99211282j
-32. +35.30655922j
-32. +32.j
-32. +29.00310941j
-32. +26.26172131j
-32. +23.73281748j
-32. +21.38171641j
-32. +19.18006188j
-32. +17.10435635j
-32. +15.13487283j
-32. +13.254834j
-32. +11.44978308j
-32. +9.70709388j
-32. +8.01558273j
-32. +6.36519576j
-32. +4.7467516j
-32. +3.15172491j
-32. +1.57205919j
-32. +0.j
-32. -1.57205919j
-32. -3.15172491j
-32. -4.7467516j
-32. -6.36519576j
-32. -8.01558273j
-32. -9.70709388j
-32. -11.44978308j
-32. -13.254834j
-32. -15.13487283j
-32. -17.10435635j
-32. -19.18006188j
-32. -21.38171641j
-32. -23.73281748j
-32. -26.26172131j
-32. -29.00310941j
-32. -32.j
-32. -35.30655922j
-32. -38.99211282j
-32. -43.14700523j
-32. -47.89138441j
-32. -53.38877458j
-32. -59.86778918j
-32. -67.65831544j
-32. -77.254834j
-32. -89.43400872j
-32. -105.48986269j
-32. -127.75116108j
-32. -160.87486375j
-32. -215.72647697j
-32. -324.9014524j
-32. -651.374964j
模值:
2016.
652.16051991
326.4735116
218.08693878
164.02658866
131.69798464
110.23661429
94.98653544
83.62002975
74.84415574
67.8833719
62.24436722
57.59847828
53.71837731
50.4418959
47.65032134
45.254834
43.18773385
41.39659414
39.84026387
38.48607276
37.30783797
36.28441823
35.39864935
34.63655041
33.98672583
33.43991136
32.98862784
32.62691706
32.35014143
32.15483432
32.03859189
32.
32.03859189
32.15483432
32.35014143
32.62691706
32.98862784
33.43991136
33.98672583
34.63655041
35.39864935
36.28441823
37.30783797
38.48607276
39.84026387
41.39659414
43.18773385
45.254834
47.65032134
50.4418959
53.71837731
57.59847828
62.24436722
67.8833719
74.84415574
83.62002975
94.98653544
110.23661429
131.69798464
164.02658866
218.08693878
326.4735116
652.16051991
相位:
0.
1.61988371
1.6689711
1.71805848
1.76714587
1.81623325
1.86532064
1.91440802
1.96349541
2.01258279
2.06167018
2.11075756
2.15984495
2.20893233
2.25801972
2.3071071
2.35619449
2.40528188
2.45436926
2.50345665
2.55254403
2.60163142
2.6507188
2.69980619
2.74889357
2.79798096
2.84706834
2.89615573
2.94524311
2.9943305
3.04341788
3.09250527
3.14159265 //python 的优化吗?这是
-3.09250527
-3.04341788
-2.9943305
-2.94524311
-2.89615573
-2.84706834
-2.79798096
-2.74889357
-2.69980619
-2.6507188
-2.60163142
-2.55254403
-2.50345665
-2.45436926
-2.40528188
-2.35619449
-2.3071071
-2.25801972
-2.20893233
-2.15984495
-2.11075756
-2.06167018
-2.01258279
-1.96349541
-1.91440802
-1.86532064
-1.81623325
-1.76714587
-1.71805848
-1.6689711
-1.61988371
注:对比可以发现CMSIS针对嵌入式平台刻意做了计算量、存储等方面的优化。
5. 在频域上以模和相角的方式还原信号
对于逆变换,也只是需要一半的数据参与即可,将FFT的输出作为IFFT的输入,如下:
void rfft_f32_test(void)
{uint16_t i;arm_rfft_fast_instance_f32 S;/* 初始化结构体S中的参数 */arm_rfft_fast_init_f32(&S, RFFT_LEN);for(i=0; i<RFFT_LEN; i++){Input_f32[i] = i;Input_f32_bak[i] = Input_f32[i];}arm_rfft_fast_f32(&S, Input_f32, Output_f32, 0);arm_rfft_fast_f32(&S, Output_f32, ifftOutput_f32, 1);printf("=====================================\r\n");for(i=0; i<RFFT_LEN; i++){printf("[%d], %f %f\r\n", i, Input_f32_bak[i], ifftOutput_f32[i]);}
}
频域上往往需要进行各种处理后,再进行逆变换,频域上以模和相位的方式重组复数点的实部虚部,再做逆变换。
理论推导:语音信号处理之预处理简述(二)_语音的帧数和帧长,帧移的关系式-CSDN博客
代码如下:
#define RFFT_LEN 64static float32_t Input_f32[RFFT_LEN];
static float32_t Input_f32_bak[RFFT_LEN];
static float32_t Output_f32[RFFT_LEN];
static float32_t mag_f32[RFFT_LEN];
static float32_t phase_f32[RFFT_LEN];static float32_t ifftInput_f32[RFFT_LEN];
static float32_t ifftOutput_f32[RFFT_LEN];void cal_phase_f32(float32_t *in_buf, float32_t *phase, uint16_t _usFFTPoints)
{float32_t real, img;uint16_t i;for (i=0; i <_usFFTPoints; i++){real= in_buf[2*i]; /* 实部 */img= in_buf[2*i + 1]; /* 虚部 *//* atan2求解的结果范围是(-pi, pi], 弧度制 */phase[i] = atan2(img, real);}
}void rfft_f32_test(void)
{uint16_t i;arm_rfft_fast_instance_f32 S;/* 初始化结构体S中的参数 */arm_rfft_fast_init_f32(&S, RFFT_LEN);for(i=0; i<RFFT_LEN; i++){Input_f32[i] = i;Input_f32_bak[i] = Input_f32[i];}arm_rfft_fast_f32(&S, Input_f32, Output_f32, 0);
// for(i=0; i<RFFT_LEN; i++)
// {
// printf("[%d], %f\r\n", i, Output_f32[i]);
// }arm_cmplx_mag_f32(Output_f32, mag_f32, RFFT_LEN);
// printf("=====================================\r\n");
// for(i=0; i<RFFT_LEN; i++)
// {
// printf("[%d], %f\r\n", i, mag_f32[i]);
// }cal_phase_f32(Output_f32, phase_f32, RFFT_LEN);
// printf("=====================================\r\n");
// for(i=0; i<RFFT_LEN; i++)
// {
// printf("[%d], %f\r\n", i, phase_f32[i]);
// }for(i=0; i <RFFT_LEN/2; i++){/* 实部 */ifftInput_f32[2*i]= mag_f32[i]*arm_cos_f32(phase_f32[i]);/* 虚部 */ifftInput_f32[2*i+1]= mag_f32[i]*arm_sin_f32(phase_f32[i]);}arm_rfft_fast_f32(&S, ifftInput_f32, ifftOutput_f32, 1);printf("=====================================\r\n");for(i=0; i<RFFT_LEN; i++){printf("[%d], %f %f\r\n", i, Input_f32_bak[i], ifftOutput_f32[i]);}
}
打印输出:
[0], 0.000000 -0.000479
[1], 1.000000 0.999496
[2], 2.000000 1.999522
[3], 3.000000 2.999496
[4], 4.000000 3.999519
[5], 5.000000 4.999496
[6], 6.000000 5.999519
[7], 7.000000 6.999498
[8], 8.000000 7.999521
[9], 9.000000 8.999496
[10], 10.000000 9.999523
[11], 11.000000 10.999493
[12], 12.000000 11.999523
[13], 13.000000 12.999498
[14], 14.000000 13.999523
[15], 15.000000 14.999496
[16], 16.000000 15.999520
[17], 17.000000 16.999496
[18], 18.000000 17.999519
[19], 19.000000 18.999496
[20], 20.000000 19.999523
[21], 21.000000 20.999496
[22], 22.000000 21.999519
[23], 23.000000 22.999496
[24], 24.000000 23.999521
[25], 25.000000 24.999496
[26], 26.000000 25.999519
[27], 27.000000 26.999500
[28], 28.000000 27.999519
[29], 29.000000 28.999496
[30], 30.000000 29.999519
[31], 31.000000 30.999496
[32], 32.000000 31.999519
[33], 33.000000 32.999496
[34], 34.000000 33.999516
[35], 35.000000 34.999496
[36], 36.000000 35.999519
[37], 37.000000 36.999496
[38], 38.000000 37.999519
[39], 39.000000 38.999496
[40], 40.000000 39.999519
[41], 41.000000 40.999496
[42], 42.000000 41.999519
[43], 43.000000 42.999500
[44], 44.000000 43.999519
[45], 45.000000 44.999496
[46], 46.000000 45.999519
[47], 47.000000 46.999496
[48], 48.000000 47.999519
[49], 49.000000 48.999496
[50], 50.000000 49.999519
[51], 51.000000 50.999496
[52], 52.000000 51.999516
[53], 53.000000 52.999496
[54], 54.000000 53.999519
[55], 55.000000 54.999496
[56], 56.000000 55.999519
[57], 57.000000 56.999496
[58], 58.000000 57.999516
[59], 59.000000 58.999493
[60], 60.000000 59.999516
[61], 61.000000 60.999496
[62], 62.000000 61.999516
[63], 63.000000 62.999496
注:short类型的音频数据和float互转,在某些场合下是不是要向上取整,以保证精度?
6. 求能量值
实际上就是求模值的平方。
文件:CMSIS\DSP\Source\ComplexMathFunctions\ arm_cmplx_mag_squared_f32.c
| 函数原型 | void arm_cmplx_mag_squared_f32( const float32_t * pSrc, float32_t * pDst, uint32_t numSamples) |
| 函数功能 | 求解复数序列的模值 |
| 参数 | pSrc:输入的复数序列,注意排序!(实部+虚部) pDst: 输出的buffer(实序列). numSamples: 输入的复数序列的长度 |
| 返回值 | Void |
| 定义处(源文件) | |
| 声明处(头文件) |
示例代码:
void rfft_f32_test(void)
{uint16_t i;arm_rfft_fast_instance_f32 S;/* 初始化结构体S中的参数 */arm_rfft_fast_init_f32(&S, RFFT_LEN);for(i=0; i<RFFT_LEN; i++){Input_f32[i] = i;Input_f32_bak[i] = Input_f32[i];}arm_rfft_fast_f32(&S, Input_f32, Output_f32, 0);
// for(i=0; i<RFFT_LEN; i++)
// {
// printf("[%d], %f\r\n", i, Output_f32[i]);
// }arm_cmplx_mag_f32(Output_f32, mag_f32, RFFT_LEN);printf("=====================================\r\n");for(i=0; i<RFFT_LEN; i++){printf("[%d], %f\r\n", i, mag_f32[i]);}arm_cmplx_mag_squared_f32(Output_f32, mag_squared_f32, RFFT_LEN);printf("=====================================\r\n");for(i=0; i<RFFT_LEN; i++){printf("[%d], %f\r\n", i, mag_squared_f32[i]);}
}
串口输出:
[16:15:51.866] =====================================
[16:15:51.914] [0], 2016.253906
[16:15:51.930] [1], 652.160522
[16:15:51.946] [2], 326.473480
[16:15:51.962] [3], 218.086929
[16:15:51.978] [4], 164.026596
[16:15:51.994] [5], 131.697983
[16:15:52.026] [6], 110.236603
[16:15:52.042] [7], 94.986534
[16:15:52.058] [8], 83.620033
[16:15:52.074] [9], 74.844154
[16:15:52.090] [10], 67.883369
[16:15:52.106] [11], 62.244362
[16:15:52.122] [12], 57.598473
[16:15:52.138] [13], 53.718376
[16:15:52.154] [14], 50.441895
[16:15:52.170] [15], 47.650322
[16:15:52.186] [16], 45.254833
[16:15:52.218] [17], 43.187737
[16:15:52.234] [18], 41.396591
[16:15:52.250] [19], 39.840263
[16:15:52.266] [20], 38.486073
[16:15:52.282] [21], 37.307838
[16:15:52.298] [22], 36.284424
[16:15:52.314] [23], 35.398647
[16:15:52.330] [24], 34.636551
[16:15:52.346] [25], 33.986725
[16:15:52.378] [26], 33.439907
[16:15:52.394] [27], 32.988617
[16:15:52.410] [28], 32.626923
[16:15:52.426] [29], 32.350151
[16:15:52.442] [30], 32.154846
[16:15:52.458] [31], 32.038574
[16:15:52.474] [32], 2.004150
[16:15:52.490] [33], 0.000000
[16:15:52.506] [34], 0.000000
[16:15:52.522] [35], 0.000000
[16:15:52.538] [36], 0.000000
[16:15:52.554] [37], 0.000000
[16:15:52.570] [38], 0.000000
[16:15:52.586] [39], 0.000000
[16:15:52.618] [40], 0.000000
[16:15:52.634] [41], 0.000000
[16:15:52.650] [42], 0.000000
[16:15:52.666] [43], 0.000000
[16:15:52.682] [44], 0.000000
[16:15:52.698] [45], 0.000000
[16:15:52.714] [46], 0.000000
[16:15:52.730] [47], 0.000000
[16:15:52.745] [48], 0.000000
[16:15:52.761] [49], 0.000000
[16:15:52.778] [50], 0.000000
[16:15:52.793] [51], 0.000000
[16:15:52.809] [52], 0.000000
[16:15:52.825] [53], 0.000000
[16:15:52.841] [54], 0.000000
[16:15:52.857] [55], 0.000000
[16:15:52.873] [56], 0.000000
[16:15:52.889] [57], 0.000000
[16:15:52.905] [58], 0.000000
[16:15:52.921] [59], 0.000000
[16:15:52.937] [60], 0.000000
[16:15:52.953] [61], 0.000000
[16:15:52.969] [62], 0.000000
[16:15:53.001] [63], 0.000000
[16:15:53.017] =====================================
[16:15:53.049] [0], 4065280.000000
[16:15:53.065] [1], 425313.312500
[16:15:53.097] [2], 106584.937500
[16:15:53.113] [3], 47561.910156
[16:15:53.129] [4], 26904.726563
[16:15:53.161] [5], 17344.359375
[16:15:53.177] [6], 12152.109375
[16:15:53.193] [7], 9022.441406
[16:15:53.209] [8], 6992.310059
[16:15:53.225] [9], 5601.647949
[16:15:53.258] [10], 4608.151367
[16:15:53.274] [11], 3874.360352
[16:15:53.290] [12], 3317.584229
[16:15:53.306] [13], 2885.664063
[16:15:53.322] [14], 2544.384766
[16:15:53.354] [15], 2270.553223
[16:15:53.370] [16], 2048.000000
[16:15:53.386] [17], 1865.180664
[16:15:53.402] [18], 1713.677734
[16:15:53.434] [19], 1587.246582
[16:15:53.450] [20], 1481.177856
[16:15:53.466] [21], 1391.874878
[16:15:53.482] [22], 1316.559326
[16:15:53.514] [23], 1253.064331
[16:15:53.530] [24], 1199.690552
[16:15:53.546] [25], 1155.097534
[16:15:53.562] [26], 1118.227295
[16:15:53.594] [27], 1088.248901
[16:15:53.610] [28], 1064.515991
[16:15:53.625] [29], 1046.532227
[16:15:53.642] [30], 1033.934204
[16:15:53.673] [31], 1026.470215
[16:15:53.689] [32], 4.016619
[16:15:53.705] [33], 0.000000
[16:15:53.721] [34], 0.000000
[16:15:53.737] [35], 0.000000
[16:15:53.753] [36], 0.000000
[16:15:53.769] [37], 0.000000
[16:15:53.785] [38], 0.000000
[16:15:53.801] [39], 0.000000
[16:15:53.817] [40], 0.000000
[16:15:53.833] [41], 0.000000
[16:15:53.849] [42], 0.000000
[16:15:53.865] [43], 0.000000
[16:15:53.881] [44], 0.000000
[16:15:53.897] [45], 0.000000
[16:15:53.913] [46], 0.000000
[16:15:53.929] [47], 0.000000
[16:15:53.945] [48], 0.000000
[16:15:53.961] [49], 0.000000
[16:15:53.993] [50], 0.000000
[16:15:54.009] [51], 0.000000
[16:15:54.025] [52], 0.000000
[16:15:54.041] [53], 0.000000
[16:15:54.057] [54], 0.000000
[16:15:54.073] [55], 0.000000
[16:15:54.089] [56], 0.000000
[16:15:54.105] [57], 0.000000
[16:15:54.121] [58], 0.000000
[16:15:54.137] [59], 0.000000
[16:15:54.153] [60], 0.000000
[16:15:54.169] [61], 0.000000
[16:15:54.185] [62], 0.000000
[16:15:54.201] [63], 0.000000
这篇关于CMSIS-DSP实数FFT相关API(单精度浮点float)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






