实数专题
SAP HCM 如何计算缺勤实数
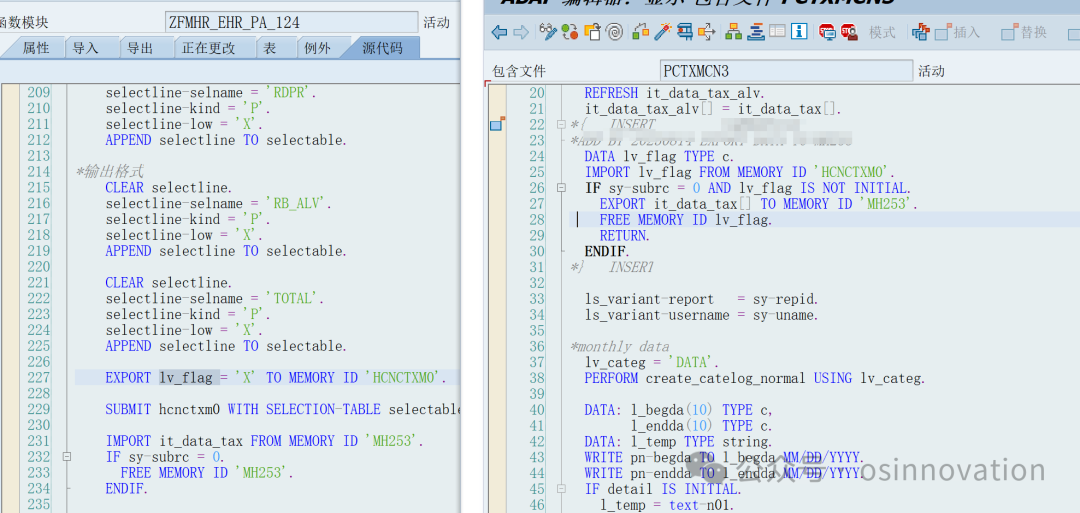
导读 INTRODUCTION 缺勤实数:这几天好几个朋友问题有什么办法可以计算出缺勤的时长,因为计算时长需要和排班去匹配,所以逻辑复杂度还是比较高的,希望有标准的函数能完成。其实SAP有个标准的函数可以完成,复杂的时候填充的参数特别多,所以今天介绍一个函数PA30保存2001的时候会调用,这样可以知道标准参数需要填充什么值。 作者:vivi,来源:osinnovation。 一、具体函数
【高中数学/极值/判别式法】已知实数a和b,b在(0,1)区间,a-b=1,则1/(a-1)+1/(5-4b)的最小值是?
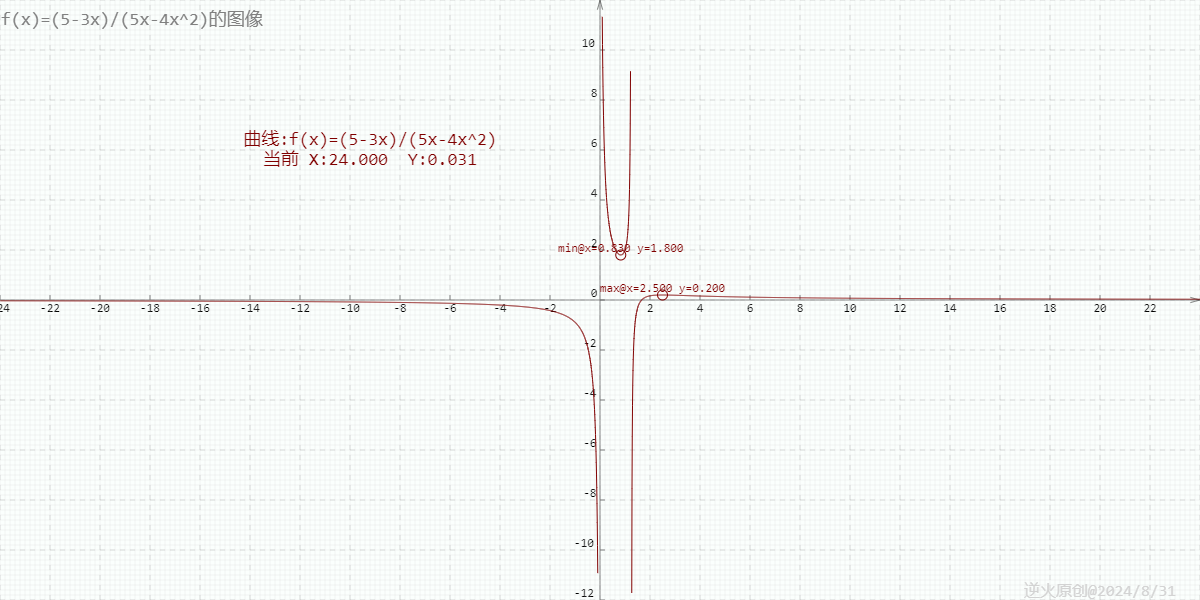
【问题】 已知实数a,b,b在(0,1)区间,a-b=1,则1/(a-1)+1/(5-4b)的最小值是? 【来源】 《解题卡壳怎么办 高中数学解题智慧点剖析》P34 余继光 苏德矿合著 浙江大学出版社出版 【破题点】 将a-1用b取代,发现结果是二次式相除,正好可用判别式法。 【解答】 由a-b=1得到a-1=b 于是原式=1/b+1/(5-4b) 设b为x,结果为y,得到表达式
实数系和复数系-习题
出去有明确的相反的说明以外,本习题中所提到的数,都理解为实数 1.如果 r ( r ≠ 0 ) r\left( r\neq 0 \right) r(r=0)是有理数而 x x x是无理数,证明 r + x r + x r+x及 r x rx rx是无理数 证明: 假设 r + x r + x r+x是有理数,则 x = r + x − r x = r + x - r x=r+x−r是有理数,矛
信号傅里叶变换后的实数和虚数部分理解
傅里叶(FFT、DFT、傅立叶、Fourier)傅里叶变换的结果为什么含有复数? 为什么傅里叶变换的结果含有复数成份? 看了很多关于FFT的资料,现在看到一个资料说FFT转换的结果是实部+虚部,所以不理解为什么从时域转到频域就会变成复数。 第一,从定义式上看,积分号里含有复数,积分结果是复数; 第二,从傅立叶变换的物理意义上看:FT变换是将一个信号分解为多个信号之和的形式,并且是正弦或余弦信号
如何理解与学习数学分析——第二部分——数学分析中的基本概念——第10章——实数
第2 部分:数学分析中的基本概念 (Concepts in Analysis) 10. 实数(The Real Numbers) 本章介绍比率数(rational numbers)和非比数(irrational numbers)及其与十进制展开的关系。讨论了实数的公理,并解释了完备性公理对于区分实数和比率数为何必不可少,并证明关于序列和函数的直观而令人信服的结果。 10.1 数的
uva 748 Exponentiation(高精度实数乘法)
题目链接:748 - Exponentiation 题目大意:高精度求次幂。 解题思路:先将小树点剔除,记录小数点的位数。然后进行高精度乘法运算(注意输出时0的剔除) #include <stdio.h>#include <string.h>const int N = 1005;int n, a[N], b[N], na, nb;int find(char *st
hdu 1753 大明A+B(实数高精度)
题目连接:1753 大明A+B 解题思路:将实数的整数部分和小数数部分分开储存, 小数部分正序储存,由两个数中小数位数最大的地方开始相加(普通的高精度加法), 注意赋值的时候要清零,这里默认没有位数的地方为零。 如果加到i =0位后任有剩, 要保留到整数为进行加法。 #include <stdio.h>#include <string.h>const int N = 405
5.1,从键盘任意输入一个实数,不使用计算绝对值函数编程计算并输出该实数的绝对值。
#include<stdio.h>main(){int a;printf("输入一个实数");scanf("%d",&a);a=sqrt(a*a);printf("%d\n",a);return 0;} 心得:学会了用函数sqrt来对一个数开方,还用到取地址符号,在c语言中该取一个数的地址时取地址符号是不可少的。
采用分治法求含n个实数序列中的最大元素和次大元素(C语言)
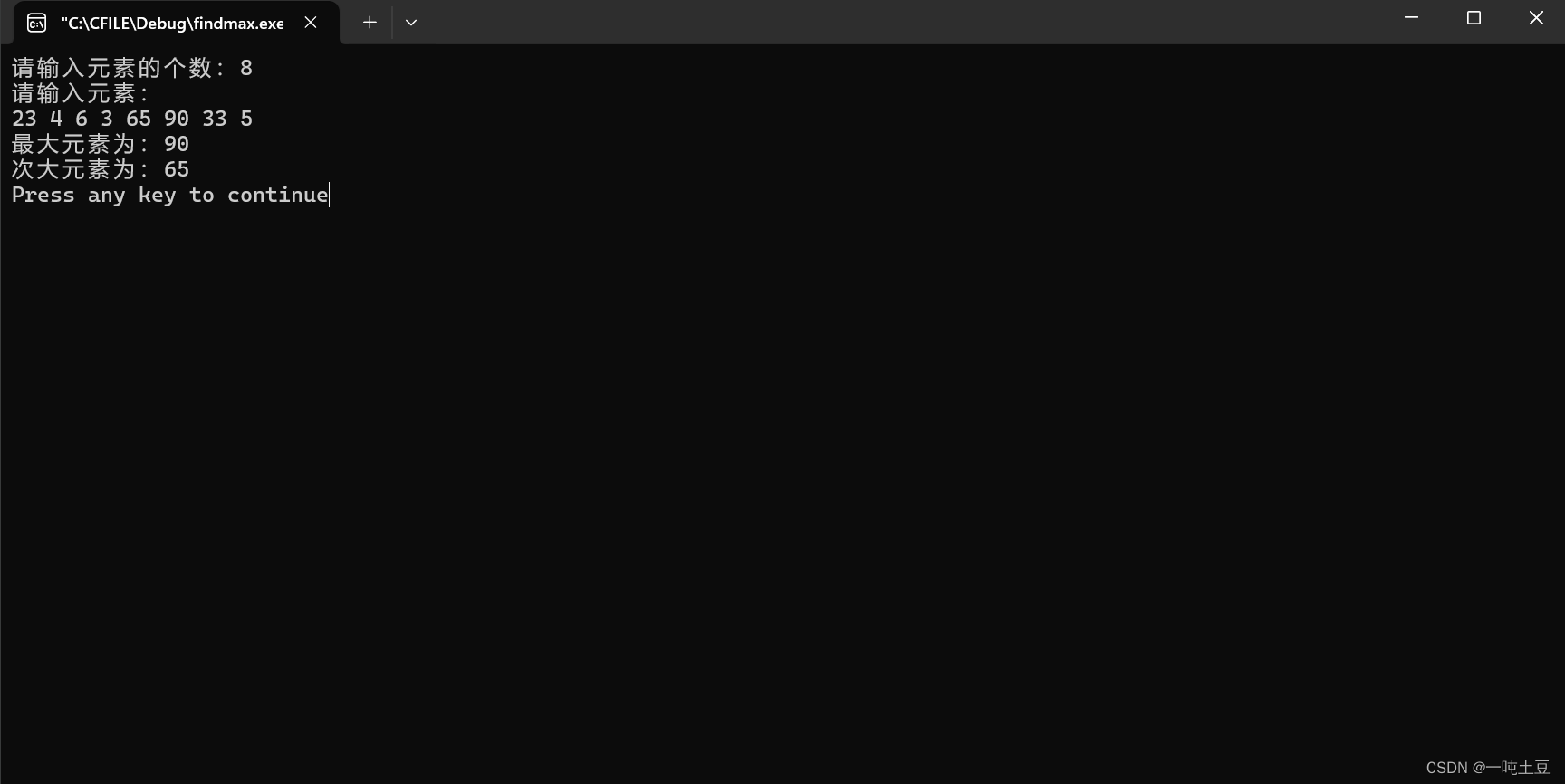
目录 实验内容: 实验过程: 1.算法设计 2.程序清单 3.复杂度分析 4.运行结果 实验内容: 设计一个程序,采用分治法求含n个实数序列中的最大元素和次大元素,并分析算法的时间复杂度。 实验过程: 1.算法设计 该程序采用递归分治策略,以下是算法设计思路的详细描述: 核心函数solve(): 基本情况:当数组只有一个元素(low == high)时,直接将
PTA 6-5 实数数组 - 数组的输出 (10 分)
6-5 实数数组 - 数组的输出 (10 分) 请编写函数,输出实数数组的元素。 函数原型 void ArrayOutput(const double *array, int size); 说明:array 为数组的起始地址,size 为数组尺寸。函数输出该数组的全部元素,元素之间以逗号和空格间隔(参见输出样例)。 裁判程序 #include <stdio.h>#include <s
PTA 6-4 实数数组 - 2. 数组的输入 (10 分)
请编写函数,输入实数数组的元素。 函数原型 void ArrayInput(double *array, int size); 说明:array 为数组的起始地址,size 为数组元素个数。函数输入该数组的全部元素,元素之间以逗号或空格分隔(参见输入样例)。 裁判程序 #include <stdio.h>#include <stdlib.h>#define arraySize 1024
C++教学——从入门到精通 5.单精度实数float
众所周知,三角形的面积公式是(底*高)/2 那就来做个三角形面积计算器吧 到吗如下 #include"bits/stdc++.h"using namespace std;int main(){int a,b;cin>>a>>b;cout<<(a*b)/2;} 这不对呀,明明是7.5而他却是7,这是什么原因呢? 其实int是整型,这能是整数而不能是小数或字符 所以又要学新的类型
二次方程式 ax**2 + bx + c = 0(用python实现,区分实数根与复数根)
import mathimport cmathdef sol(a,b,c):#判断b的平方是否大于4ac,大于等于的时候是实数根,小于的时候是复数根(cmath相比与math的区别是cmath是复数运算)if b**2 >= 4*a*c :sqrt = math.sqrt(b**2 - 4*a*c)x1 = (-b + sqrt) / (2 * a)x2 = (-b - sqrt) / (2 *
在没有康托尔对角化方法的情况下证明实数的不可数性
乔治·康托尔 |图片来源: 维基百科 一、说明 对于那些对数学感兴趣的人来说,无穷大实际上可以有不同的大小,这可能是一个众所周知的事实。事实上,最著名的例子是所有实数的集合比所有自然数的集合“大”。你可能知道,这实际上有一个非常优雅的证明,称为康托尔对角线方法,由乔治·康托尔在1891年提出。如果您不知道这一点,我绝对建议您研究一下,因为我认为该方法非常聪
每日一题:C语言经典例题之实数的整数部分
题目描述 输入一个实数,输出实数的整数部分。注意该实数的位数不超过100位。输入的整数部分可能含有不必要的前导0,输出时应去掉,当然,若整数部分为0,则该0不能去掉。如输入0023.56732,输出应为23,而不是0023;0.123对应的输出应为0。当然输入也可能不含小数部分。 输入 输入一个实数。 输出 输出实数的整数部分。 样例输入: 0023.56732 样例输出: 23 代码: #
每日一题:C语言经典例题之实数的小数部分
题目描述 输入一个实数,输出该实数的小数部分,小数部分若多余的末尾0,请去掉。如输入111111.12345678912345678900则输出0.123456789123456789。若去掉末尾0之后小数部分为0,则输出“No decimal part”。注意该实数的位数不超过100位。 输入 输入一个实数。 输出 输出该实数的小数部分。 样例输入: 111111.12345678912
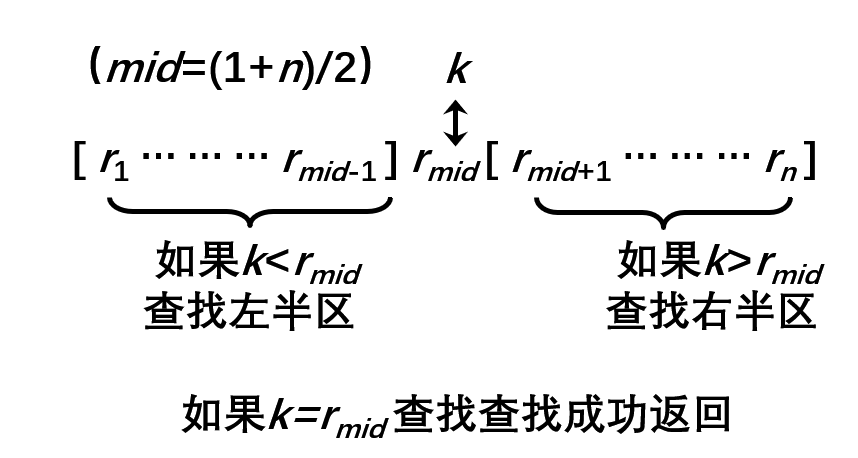
【No.13】蓝桥杯二分查找|整数二分|实数二分|跳石头|M次方根|分巧克力(C++)
二分查找算法 知识点 二分查找原理讲解在单调递增序列 a 中查找 x 或 x 的后继在单调递增序列 a 中查找 x 或 x 的前驱 二分查找算法讲解 枚举查找即顺序查找, 实现原理是逐个比较数组 a[0:n-1] 中的元素,直到找到元素 x 或搜索整个数组后确定 x 不在其中。最坏情况下需要比较 N 次,时间复杂度是 O(n),属于线性阶算法。 而二分查找是一种折半查找方法。 该方法将 N
js比较a,b大小,按从小到大的顺序输出这两个实数。
1.//比较a,b大小,按从小到大的顺序输出这两个实数。 2.程序 <script> var a,b,c; a=3.8;b=3; if(a<b){ document.write(a+'<'+b); }else{ c=a; a=b; b=c; document.write(a+'<'+
数学分析(一)-实数集与函数3-函数概念6-初等函数4-三角函数6:arccotx【cotx的反函数】【减函数】【定义域:(-∞,+∞);值域:(0,π)】【arccot0=π/4】
高中数学,三角函数的图像与性质 系统化,轻快学习高中数学三角函数的图像、性质及其变换必备知识 精准狠——三角函数图像及其性质 三角函数与反三角函数(图像)
复变函数论(一)-复数与复变函数01-复数02:复平面【复数z=x+iy由一对有序实数(x,y)唯一确定;(x,y) 就称为复数z的实数对形式】【表示复数z的平面称为复平面;x轴:实轴;y轴:虚轴】
一个复数 z = x + i y z=x+\mathrm{i} y z=x+iy 本质上由一对有序实数 ( x , y ) (x, y) (x,y) 惟一确定, ( x , y ) (x, y) (x,y) 就称为复数 z z z 的实数对形式. 于是能够建立平面上全部的点和全体复数间的一一对应关系. 换句话说, 我们可以借助于横坐标为 x x x 、纵坐标为 y y y 的点
求实数绝对值 (sdut oj)
求实数绝对值 Time Limit: 1000MS Memory Limit: 65536KB Problem Description 求实数的绝对值。 Input 输入数据有多组,每组占一行,每行包含一个实数。输入文件直到EOF为止! Output 对于每组输入数据,输出它的绝对值,要求每组数据输出一行,
计算机科学与导论 第三章数据存储(第二部分存储实数)
文章预览: 1. 存储实数1.1.浮点表示法1.2.规范化1.3. 符号,指数,尾数1.4. 余码系统1.5. IEEE1.6. IEEE标准浮点数的存储1.7. 将存储IEEE标准浮点数的数字还原1. 8.上溢和下溢1.9. 存储01.10 截断错误 2. 存储文本2.1. ASCII2.2 unicode 3. 存储音频3.1 采样3.2 量化3.3 编码3.3.1. 每样本位3.3.2
初中数学题目(实数) - 第五小题解答
§05 第五小题 若 1 − 2 x 3 + 3 y − 2 3 = 0 \sqrt[3]{1 - 2x} + \sqrt[3]{3y - 2} = 0 31−2x +33y−2 =0,且 y ≠ 0 y \ne 0 y=0,求 2 x + 1 y {{2x + 1} \over y} y2x+1的值。 ※ 解答 ▲ 图1 第五小题答案
MATLAB初始化种群-随机和一定的实数序列
在智能算法的编码场景中,很多时候是需要用求和为一定的编码的, 比如分配问题, 配送问题等, 下面给出具体程序代码: clc;close all;clear all;warning off;%清除变量 rand('seed', 100); randn('seed', 100); format long g; N=5; % 设定优化问题维数 lb=0*ones(1,N);% 自变量上限 ub=1