【No.13】蓝桥杯二分查找|整数二分|实数二分|跳石头|M次方根|分巧克力(C++)

本文主要是介绍【No.13】蓝桥杯二分查找|整数二分|实数二分|跳石头|M次方根|分巧克力(C++)，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

二分查找算法

知识点

• 二分查找原理讲解
• 在单调递增序列 a 中查找 x 或 x 的后继
• 在单调递增序列 a 中查找 x 或 x 的前驱

二分查找算法讲解

枚举查找即顺序查找，
实现原理是逐个比较数组 a[0:n-1] 中的元素，直到找到元素 x 或搜索整个数组后确定 x 不在其中。最坏情况下需要比较 N 次，时间复杂度是 O(n)，属于线性阶算法。
而二分查找是一种折半查找方法。
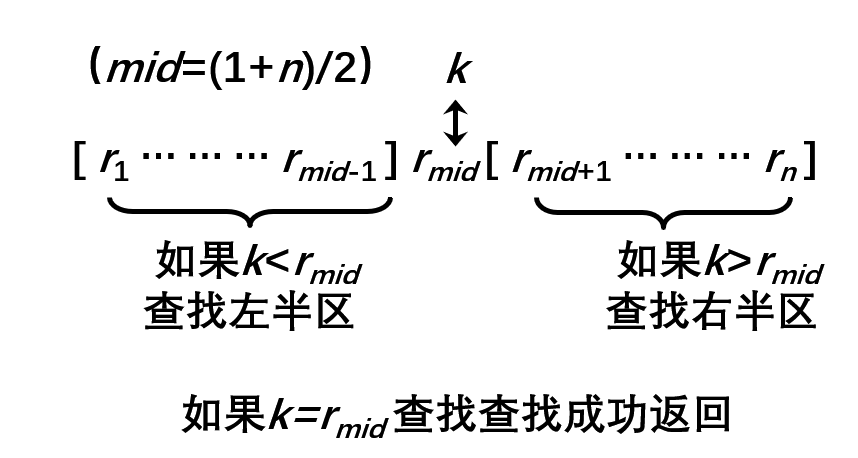
该方法将 N 个元素分成大致相等的两部分，选取中间元素与查找的元素进行比较。

• 如果相等，则查找成功；
• 如果查找元素小于中间元素，则在左半区继续查找；
• 如果查找元素大于中间元素，则在右半区继续查找。
  每次都将范围缩小至原来的一半，因此时间复杂度是 $O({\log }_{2}n)$。
  需要注意的是，二分查找的前提是数组有序，一般是从小到大排列。
  折半查找的基本思想：
  在有序表中（low, high, low<=high），取中间记录即 a[(high+low)/2] 作为比较对象。
• 若给定值与中间记录的关键码相等，则查找成功。
• 若给定值小于中间记录的关键码，则在中间记录的左半区继续查找。
• 若给定值大于中间记录的关键码，则在中间记录的右半区继续查找。
  不断重复上述过程，直到查找成功，或所查找的区域无记录，查找失败。
  二分查找的特征：

1. 答案具有单调性。
2. 二分答案的问题往往有固定的问法，例如：令最大值最小（最小值最大），求满足条件的最大（小）值等。
   折半查找一般过程：
   

Step 1:假设存在一个有序数组：
下标[ 0   1   2   3   4   5   6   7   8    9    10   11   12 ]
数据[ 7   14  18  21  23  29  31  35   38   42   46   49  52 ]↑                                                   ↑low=0                                              high=12mid=(low+high)/2mid=(0+12)/2mid=6[mid]=31 > 14，所以选择左半部分操作：此时令low不变，high=mid-1=5Step 2:下标[ 0   1   2   3   4   5   6   7   8    9    10   11   12 ]
数据[ 7   14  18  21  23  29  31  35   38   42   46   49  52 ]↑                   ↑low=0                 high=5mid=(low+high)/2mid=(0+6)/2mid=3[mid]=21 > 14，所以选择左半部分操作：此时令low不变，high=mid-1=2Step 3:下标[ 0   1   2   3   4   5   6   7   8    9    10   11   12 ]
数据[ 7   14  18  21  23  29  31  35   38   42   46   49  52 ]↑       ↑low=0    high=2mid=(low+high)/2mid=(0+2)/2mid=1[mid]=14 = 14  找到答案操作：返回下标

整数二分法常用算法模板

// 在单调递增序列a中查找>=x的数中最小的一个（即x或x的后继）
while (low < high)
{int mid = (low + high) / 2;if (a[mid] >= x)high = mid;elselow = mid + 1;
}// 在单调递增序列a中查找<=x的数中最大的一个（即x或x的前驱）
while (low < high)
{int mid = (low + high + 1) / 2;  //向右+1个，以便于判断区间的时候落到右侧// int mid = left + (right - left) / 2;if (a[mid] <= x)low = mid;elsehigh = mid - 1;
}

此处我们先分整数的二分查找法的常用模版，关于实数的部分，我们后面再讲。

为什么采用这一套代码的而不是采用查找等于的 X

是因为这样的适用范围更广，当有 X 时这套代码就返回 X 的位置。如果没有 X，就返回 <=x 的数中最大的一个或者 >=x 的数中最小的一个。

跳石头

【题目描述】
“跳石头"比赛在一条笔直的河道中进行，河道中分布着一些巨大岩石。组委会已经选择好了两块岩石作为比赛起点和终点。在起点和终点之间，有n块岩石(不含起点和终点的岩石)。在比赛过程中，选手们将从起点出发，每一步跳向相邻的岩石，直至到达终点。
为了提高比赛难度，组委会计划移走些岩石，使得选手们在比赛过程中的最短跳跃距离尽可能长。由于预算限制，组委会至多从起点和终点之间移走m块岩石(不能移走起点和终点的岩石)
【输入描述】
输入文件第一行包含三个整数L，N，M，分别表示起点到终点的距离，起点和终点之间的岩石数，以及组委会至多移走的岩石数。
接下来 N行，每行一个整数，第 i行的整数 Di(0<Di<L)表示第 i 块岩石与起点的距离。这些岩石按与起点距离从小到大的顺序给出，且不会有两个岩石出现在同一个位置。
其中，0≤M≤N≤5x10^{4，1≤L≤10}9
【输出描述】
输出只包含一个整数，即最短跳跃距离的最大值。

题目解析

二分法套路题：最小值最大化，最大值最小化
在n块岩石中移走m个石头，有很多种移动方法
在第i种移动方法中，剩下的石头之间的距离，有一个最小距离ai.
在所有移动方法的最小距离ai中，问最大的ai是多少
在所有可能的最小值中，找最大的那个，就是最小值最大化

在单调递增的序列中，找到满足某个条件的最大的那个值

1. 暴力法：找所有的组合，在n块岩石中选m个石头的组合，情况太多，超时
2. 二分思路：不找搬走石头的组合，而是给出一个距离d，检查能不能搬走m块石头而得到最短距离d。把所有的d都试一遍，肯定能找到一个最短的d，用二分法找这个d

最短距离ai，最小可以取到0，最大可以取到L，不管用什么方法，ai一定是这个区间上的一个数
这个区间是一个递增的，有序的，
二分这个区间，找到一个ai，检查这个ai是不是符合题意：是不是能通过n块岩石中移走m块岩石能构造出，最短距离是ai的这么一种情况

如何判断能否通过n块石头中一走m块石头来实现

比如说现在要找的ai是3，有5块石头，它们之间的距离是5，3，4，2，显然5，3，4满足条件，但是2不满足，所以要移走第四块石头，变成5，3，6，可以通过这样的方法来判断是否要移走某块石头
满足了3以后，因为要找最大的，所以解下来判断4，这一组石头里的3就不符合了，移走第二块石头，变成8，6，这样就需要移走两块石头
如果m=2的话，就满足条件，如果m=1就不满足
所以m=1的话，ai就只能是3，m=2的话，可以是4

1. 如果是用暴力法去找的话，就是从1开始一直枚举到L
2. 1~L是一个有序的枚举，所以可以通过二分去做
   1~L。找mid，看这个mid能不能通过移走m块来实现，可以的话，就在右边的区间继续去找，不能移走的话，就从左区间开始找

代码

#include <cstdio>
int len, n, m;
int stone[50005];
bool check(int d)  //检查距离d是否合适
{int num = 0;  //num记录搬走石头的数量int pos = 0;  //当前站立的石头for (int i = 1; i <= n; i ++){if (stone[i]-pos < d)num++;  //第i块石头可以搬走elsepos = stone[i];  //第i块石头不能搬走}if (num <= m)return true;  //要移动的石头比m少，满足条件elsereturn false;  //要移动的石头比m多，不满足条件
}int main()
{scanf("%d%d%d", &len, &n, &m);for (int i = 1; i <= n; i ++){scanf("%d", &stone[i]);}int L = 0, R = len, mid;while (L < R){mid = (L + R + 1) / 2;//查找满足条件的最大的那个值，所以向右贪心if (check(mid)){L = mid;  //满足条件，说明mid小了，调大一点}elseR = mid - 1;  //不满足条件，说明mid大了，调小一点}printf ("%d\n", L);return 0;
}

M 次方根

题目描述:
小 A 最近在学高等数学，他发现了一道题，求三次根号下27​。现在已知，小 A 开始计算，1 的三次方得1，2 的三次方得8，3 的三次方得27，然后他很高兴的填上了3。
接着他要求5次根号下164​。然后他开始1 的三次方得1，2 的三次方得8，3 的三次方得27…
直到他算到了秃头，也没有找到答案。
这时一旁的小 B 看不下去了，说这题答案又不是个整数。小 A 震惊，原来如此。作为程序高手的小 A，打算设计一个程序用于求解M次根下N的值。
但是由于要考虑精度范围，答案必须要保留7位小数，连三次根号下27都要掰手指的小 A 又怎么会设计呢。请你帮小 A 设计一个程序用于求解 M 次根号N。
数据范围：
1≤N≤1e5
1≤M≤100
M < N
要求输入:

输入描述:
第一行输入整数 N 和 M，数据间用空格隔开。

要求输出：

输出描述:
输出一个整数，并保留 7 位小数。

样例:

输入样例：
27 3
输出样例：
3.000000

运行限制:

最大运行时间：1s
最大运行内存: 256M
注意：
1. 请严格按要求输出，不要画蛇添足地打印类似：“请您输入…” 的多余内容。
2. 不要调用依赖于编译环境或操作系统的特殊函数。
3. 所有依赖的函数必须明确地在源文件中。
4. 不能通过工程设置而省略常用头文件。

题目分析

根据前面的知识，我们要找到一个具有单调性的数列，去二分。这个题的关键是我们要去二分什么，这里可以二分的是 a^M 中的 a，所以我们要先想办法设计出用于处理实数二分的代码。
这里给大家两个模板，都可以大家选择一个使用即可：

//模版一：实数域二分，设置eps法//令 eps 为小于题目精度一个数即可。比如题目说保留4位小数，0.0001 这种的。那么 eps 就可以设置为五位小数的任意一个数 0.00001- 0.00009 等等都可以。//一般为了保证精度我们选取精度/100 的那个小数，即设置 eps= 0.0001/100 =1e-6while (l + eps < r)  //l加上这个精度<r，就继续二分
//如果不小于r，就说明l-r<eps，代表这两个数之间的精度差距不会超过0.0001，代表找到这个值了
{double mid = (l + r) / 2;if (pd(mid))r = mid;elsel = mid;
}//模版二：实数域二分，规定循环次数法
//通过循环一定次数达到精度要求，这个一般 log_2 N < 精度即可。N 为循环次数，在不超过时间复杂度的情况下，可以选择给 N 乘一个系数使得精度更高。
//为什么循环100次一定可以，二分是每次除以2，除100次2，也就是做100次log_2n，1024是10次。10^6约20次，10^9约30次，所以100次一定可以满足for (int i = 0; i < 100; i++)
{double mid = (l + r) / 2;if (pd(mid))r = mid;elsel = mid;
}

模板讲完了，然后我们就要考虑判定条件了，怎样判定是否存在满足大于平均值的区间。当然这个题你可以使用语言中自带开方软件，但是我们还是联系一下实数的二分代码。
关于判定条件，我们应该设计一个代码用于比较 a^m 和 N 的大小关系。
在我们代码中：

if (pd(mid))r = mid;
elsel = mid;

pd 成功的情况，一定是 pd 的mid 符合条件，且小于 mid 的一定符合条件。因此我们要在大于mid 中继续查找，找到更大的mid。
所以我们可以设计出如下判定条件:

double pd(double a,int m)
{double c=1;while(m>0)  //计算a的m次方{c=c*a;m--;}if(c>=n) return true;elsereturn false;
}

代码解答

#include <cstdio>
#include <iostream>
#include<iomanip> //用于浮点数输出
using namespace std;double n,l,r,mid;
double eps=1e-8;bool pd(double a,int m)
{double c=1;while(m>0) {c=c*a;m--;}if(c>=n)  //return true;elsereturn false;
}int main()
{int m;cin>>n>>m;
//设置二分边界l=0,r=n;//实数二分while (l + eps < r){double mid = (l + r) / 2;if (pd(mid,m))r = mid;elsel = mid;}cout << fixed << setprecision(7) << l;//一般使用print//printf("%x.yf",n)//其中X是固定整数长度，小数点前的整数位数不够，会在前面补0//y是保留小数位数，不够补零//printf("%.7f",l);return 0;
}

分巧克力

2017 年省赛真题链接。
题目描述: 儿童节那天有 K 位小朋友到小明家做客。小明拿出了珍藏的巧克力招待小朋友们。
小明一共有 N 块巧克力，其中第 i 块是 Hi​×Wi 的方格组成的长方形。为了公平起见，
小明需要从这 N 块巧克力中切出 K 块巧克力分给小朋友们。切出的巧克力需要满足：

1. 形状是正方形，边长是整数;
2. 大小相同;
   例如一块 6x5 的巧克力可以切出 6 块 2x2 的巧克力或者 2 块 3x3 的巧克力。
   当然小朋友们都希望得到的巧克力尽可能大，你能帮小明计算出最大的边长是多少么？
   输入描述:
   第一行包含两个整数 N,K (1≤N,K≤10^5)。
   以下 N 行每行包含两个整数 Hi​,Wi​ (1≤Hi​,Wi​≤10^5)。
   输入保证每位小朋友至少能获得一块 1x1 的巧克力。
   输出描述:
   输出切出的正方形巧克力最大可能的边长。
   输入输出样例:
   示例:

输入

2 10 6 5 5 6

输出

2

运行限制:

• 最大运行时间：2s
• 最大运行内存: 256M
  注意：

1. 请严格按要求输出，不要画蛇添足地打印类似：“请您输入…”的多余内容。
2. 不要调用依赖于编译环境或操作系统的特殊函数。
3. 所有依赖的函数必须明确地在源文件中
4. 不能通过工程设置而省略常用头文件。

题目分析

简单思路，边长的最大规模为 100000；我们可以枚举出所有的情况。按从大到小的顺序进行切割，直到找到满足要求的巧克力边长。
在判断边长是否满足条件时：求一块长方形（h∗w）最多被分成的正方形（len∗len）巧克力个数为：
cnt=(h/len)∗(w/len)
但是使用朴素算法枚举时间复杂度O(n)∗O(n)=O(n^2) 会超时，所以改用 2 分查找法，这找到符合要求的最大的一个。
即用在单调递增序列 a 中查找 <=x 的数中最大的一个（即 x 或 x 的前驱）即可，原本这里的条件是 <=x ，我们将其换成验证即可。

代码解答

#include<bits/stdc++.h>using namespace std;
const int MAXN=100010;
int n,k;
int h[MAXN],w[MAXN];bool pd(int l)
{int sum=0;for(int i=0; i<n; i++){sum+=(h[i]/l)*(w[i]/l);if(sum>=k){return true;}}return false;
}int main()
{cin>>n>>k;for(int i=0; i<n; i++)cin>>h[i]>>w[i];//找到二分查找的上界int high=0;for(int i=0; i<n; i++){high=max(high,h[i]);high=max(high,w[i]);}// 二分下届由题意可得至少为1int low=1;// 由于本题目就是求符合要求的Mid 值所以要将mid定义在二分查找外边int mid=0;while(low<high){mid = (low + high+1) / 2;if(pd(mid))low=mid;elsehigh = mid - 1;//        cout<<low<<" "<<high<<endl;}//因为low=high所以输出哪一个都一样cout<<low;return 0;
}

这篇关于【No.13】蓝桥杯二分查找|整数二分|实数二分|跳石头|M次方根|分巧克力(C++)的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---