机器人学习笔记（2） 刚性运动和齐次变换

2019/10/22
2.1 位置的表示方法
几何推理的方法：合成方法、分析方法。

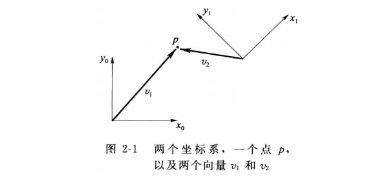
点在坐标系的表示：
点P在两个坐标系中表示如下，其中右上角表示的为所在坐标系。

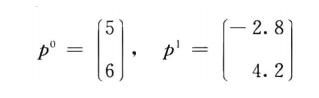
坐标系相对坐标系的表示：第一项表示的为坐标系x1y1o1相对xyo的坐标。

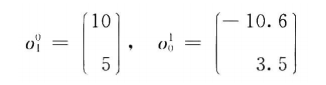
2.2 旋转的表示方法
2.2.1 平面内的旋转

二维空间中，坐标系o1x1y1的各轴线（单位向量）被投影到坐标系o0x0y0（参考坐标系）,旋转矩阵：

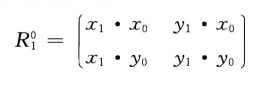
相反：

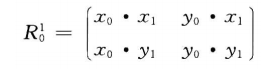
由于向量的点积服从交换律，因此有

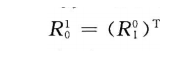
2.2.2 三维空间中内旋转
三维空间中，坐标系o1x1y1的各轴线（单位向量）被投影到坐标系o0x0y0（参考坐标系）,旋转矩阵：

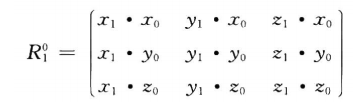
绕z轴旋转

Rz,θ具有的性质：

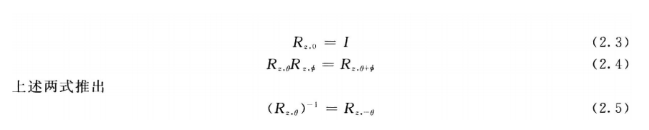
绕x轴和y轴旋转

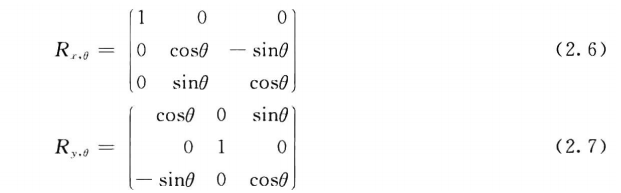
2.3 旋转变换
在坐标系o1x1y1中p坐标表示为：

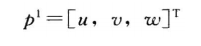
p满足：

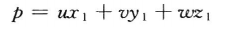
将p投影到o0x0y0中：

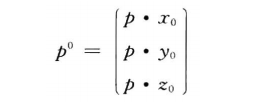
联立方程：

左边的矩阵为

坐标的矩阵为o1x1y1相对o0x0y0的姿态矩阵

旋转矩阵可以用三种不同的方式解释：（具体的解释根据题意）

2019/10/23
2.3.1 相似变换

在不同坐标系中表示相同的变换
2.4 旋转的叠加
2.4.1 相对于当前坐标的旋转
旋转的叠加定律：

我们称旋转发生时围绕的那个坐标系为当前坐标系（即可能不是针对一个固定坐标系而言）。此时矩阵相乘的顺序是右乘（后乘）。

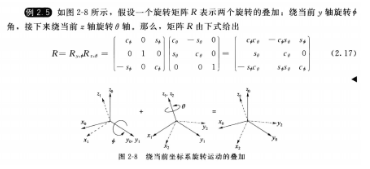
2.4.2 相对于固定的坐标系的旋转
此时矩阵相乘的顺序是左乘（前乘）。
2.4.3 旋转变换的叠加定律
即对上面叠加的总结：“当前后乘，固定左乘”
2.5 旋转的参数化

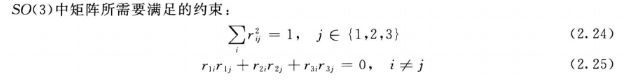
因为列向量是单位向量，各列相互正交。（1,0,0)(0,1,0)=10+01+00=0;
上面的约束一起定义了6个独立的方程，其中有9个未知数，这意味着其中的自由变量数目为3。（即想完全表达两个的坐标的系的关系需要知道三个变量）
有三种方式来表达任意旋转，任何一种方式都需要三个独立变量：欧拉角、滚动-俯仰-偏航（roll-pitch-yaw）表示法、转轴/角度表示法。
2.5.1 欧拉角

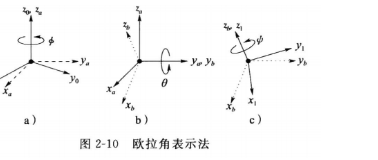
即用三个角度来表示坐标系o1x1y1z1相对于坐标系o0x0y0z0的姿态，这三角度都是相对于当前的坐标系而言，因此为后乘，用旋转矩阵表示图示变换为：

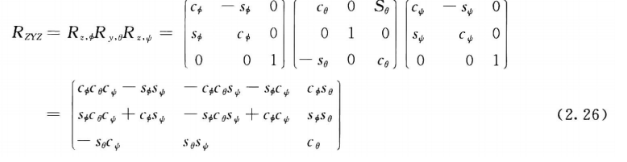
（2.26）也称ZYZ-欧拉角变换。
如何根据特定的矩阵求解角度（待补充）
2.5.2 滚动角、俯仰角和偏航角

2019/10/24
2.5.3 转轴/角度表示
利用相似变换的使得绕某轴K的旋转变换成在原有坐标系的相同的旋转。


2.6 刚性运动
定义：刚性运动是一个有序对（d,R）,其中d∈R³，R∈SO(3)。所有刚性运动组成的群被称为特殊欧式群，记为SE(3)。SE(3)=R³xSO(3).

2.7 齐次变换