本文主要是介绍Unity 布料仿真笔记1 弹簧质点模型,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
前言
万物皆可盘
弹簧质点模型
我们要在三维中仿真物理世界,那么就要将物理世界中的原理在三维场景中进行建模。也就是使用数学描述去反馈自然界中的一些现象。弹簧质点(Sping-Mass)模型是一个经典的物理学仿真模型。而弹簧质点就能够用在布料仿真、一些粒子系统中。
弹簧质点模型的思路很简单:
- 所有的节点都是一个质点
- 节点之间的连线就是一个弹簧
- 节点之间的受力通过经典力学公式计算
- 弹簧受力通过胡可定律计算
知道这个之后我们就能够分析如何在Unity中去实现一个三维仿真算法。
当我们实现一个弹簧模型之后,接下来去做布料仿真效果就很容易。
分析
从头开始
最简单的弹簧质点模型莫过于两个质点之间连接一个弹簧,我们将会用这种最简单的方式来分析。
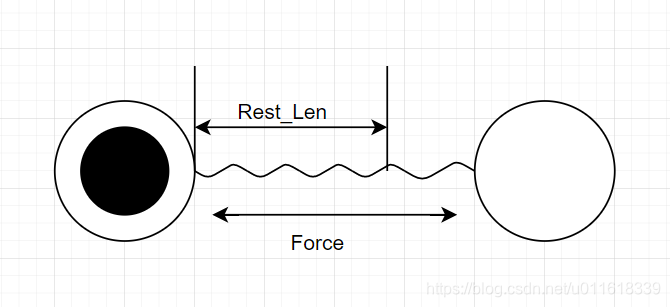
根据牛顿力学定律,力的作用是相互的,当我们右边的小球移动,就会带动弹簧拉伸,而拉伸之后的弹簧就会产生一个“还原”的力,使右边的小球受到弹簧向左拉的力。而左边的小球会受到弹簧向右拉的力。如果上面的画面不直观,那么可以想象一下,如果我们用两只手分别拿着一根弹簧的两端。当两只手往外拉的时候,两只手都会感觉弹簧在往里收缩,而且拉的越长,往里收缩的力就越大。而如果我们往里挤,那么也会感觉到,挤得越近,弹簧往外伸展的力就越大。
这里我们考虑一个理想弹簧,那么弹簧不管拉伸成什么样,或者挤压成什么样,都还是能遵循最初的胡克定律。当然如果我们添加一些弹簧的拉伸阈值或者挤压阈值(弹性限度),那么我们能够仿真更真实的效果。例如我们可以仿真布料被拉坏的效果。
胡克定律
胡克定律用17世纪英国物理学家罗伯特·胡克的名字命名[1]。其力的大小与伸长量或收缩量线性成正比。
公式为:
F = − k ⋅ Δ x F=-k\cdot \Delta x F=−k⋅Δx
Δ x \Delta x Δx是两个长度的差值,现在长度和 r e s t l e n rest_len restlen的长度。如果 Δ x \Delta x Δx越大,那么力也就越大。从公式可以看出,如果我们单纯从一个方向看,那么质点所受到的力是相反方向。
非常简单一个公式。接下来结合其他力,做一次力学仿真。
单纯受力分析
假设我们的弹簧,现在是躺在地上,那么地面的支撑力和重力抵消,同时我们假设地面绝对平滑,没有摩擦力。

左边的弹簧在拉伸的时候,会受到一个向左的力
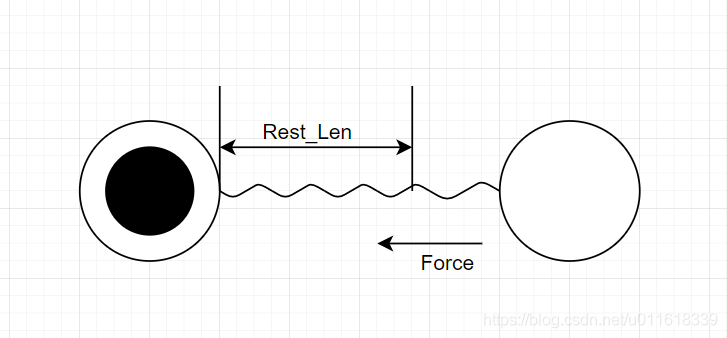
因此会导致在速度为0的时候,会向左运动。当向左弹簧的长度小于Rest_len的时候,小球会受到向右的力,逐渐减速。
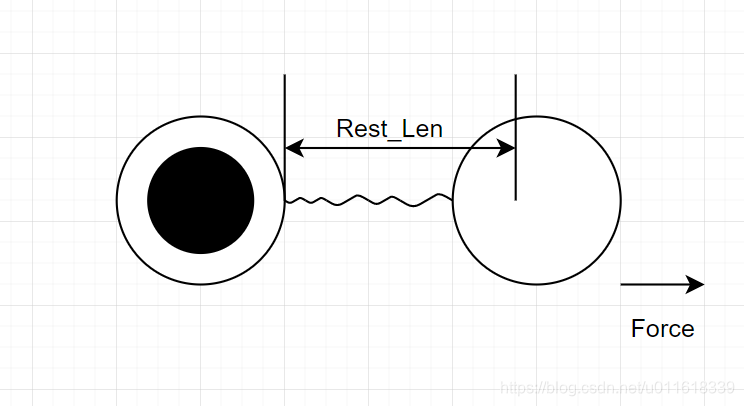
接下来,假设我们没有地面。这是一个挂在空中的小球。那么它会额外受到一个重力。
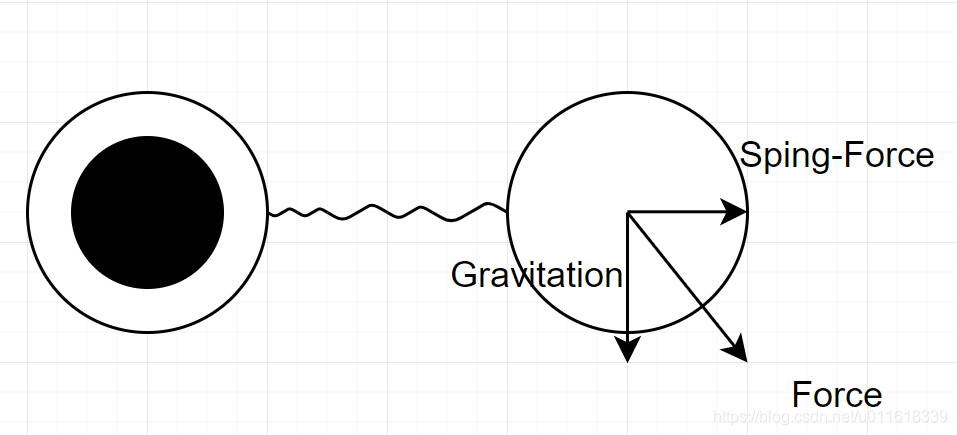
重力会使我们的小球自然向下掉落,同时也会带动弹簧拉伸。于是仿真效果就如同在弹簧上挂了一个小球。

如同没有添加小球时效果一样,小球会沿弹簧方向不断做往复运动。公式如下:
F = − k ⋅ Δ x + F g F=-k\cdot \Delta x+F_{g} F=−k⋅Δx+Fg
根据牛顿第二定律,物体的加速度与物体受的合力成正比。
F = m a F=ma F=ma
而加速度的大小会决定速度的大小,已知:
V t = V t − 1 + a Δ t V_{t}=V_{t-1}+a \Delta t Vt=Vt−1+aΔt
从公式上可以分析得到:已知速度、已知时间长度、已知受力,我们就可以大致去仿真一个弹簧质点模型。
这是大家需要考虑一个问题:弹簧在长度不断变化的过程中,弹力也在不断变化,那么质点所受的力会一直变化。难道有使用定积分这样的工具来计算吗?那么我们如何去计算在一个变化过程中的弹簧的受力过程呢。
其实不然,虽然弹簧是这样一个过程,但是我们可以用一些其他方法来计算:例如欧拉积分、Verlet积分、龙格库塔积分等方法。可以去近似逼近定积分结果。
积分
有了最基本的数学分析之后,我们需要将该算法与实际速度、位置等数据进行推导。这里使用的两种工具:欧拉积分、维特积分。当然对于这两种分析,网上有非常多的详细的论证,这里就不展开将。如果后面有时间,翻译一些国外的资料过来。
欧拉积分
欧拉积分其实分为隐式欧拉和显式欧拉,为了简单开发,这里使用显式欧拉方法进行积分。欧式积分,其实可以看成我们假定在一个规定的时间,物体的速度是一致的。那么在这个一致速度的时间范围内,我们就能很好去求解质点下一刻的状态。
V t + 1 = V t + a Δ t V_{t+1}=V_{t} + a \Delta t Vt+1=Vt+aΔt
X t + 1 = X t + V t Δ t X_{t+1}=X_{t} + V_{t} \Delta t Xt+1=Xt+VtΔt
Verlet 积分
Verlet积分参考
Verlet积分会使用上一个时刻的状态来推下一个时刻的状态。
X t + 1 = X t + ( X t − X t − 1 ) + a t ∗ Δ t ∗ Δ t X_{t+1}=X_{t} + (X_{t}-X_{t -1})+a_{t} *\Delta t*\Delta t Xt+1=Xt+(Xt−Xt−1)+at∗Δt∗Δt
实现结果
Verlet积分
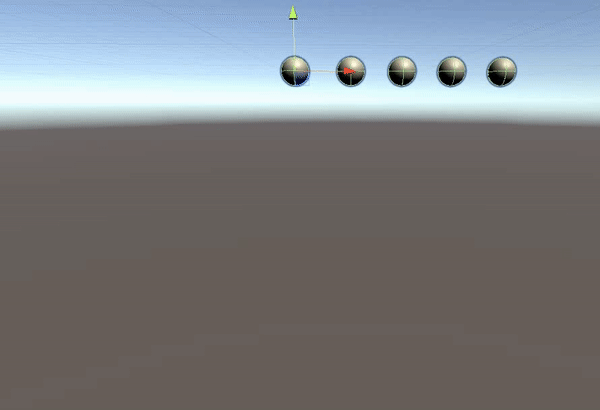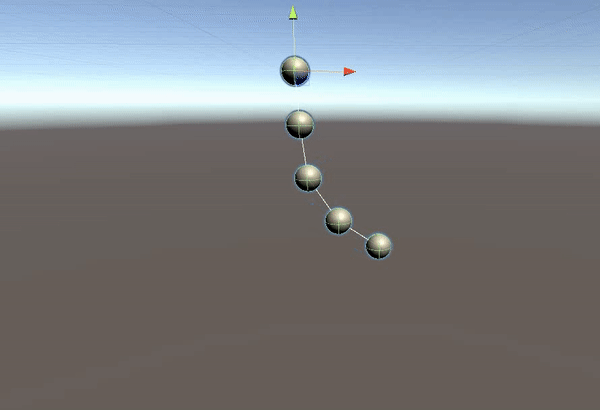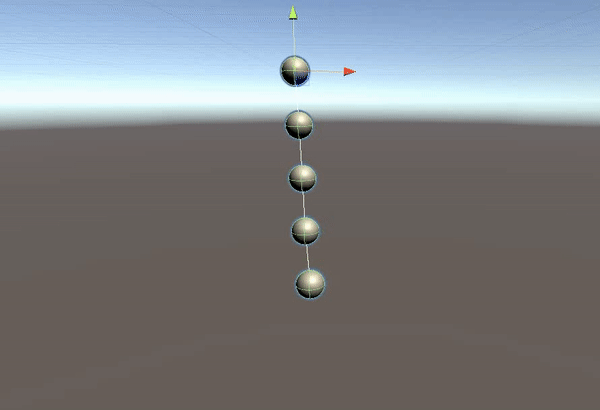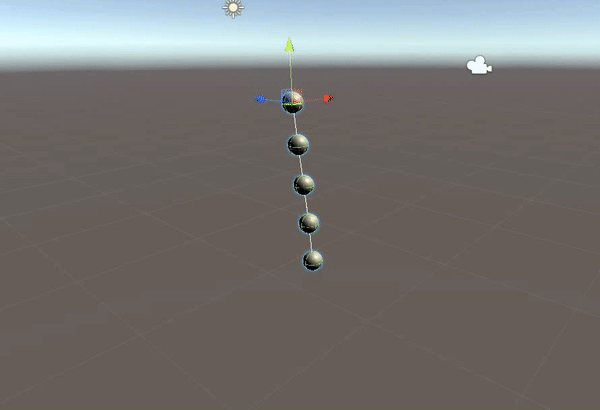
显式欧拉积分

总结
两种方法其实都挺简单的,但是实现效果还不错。接下来将会对代码进行说明。然后利用龙格库塔积分方法,去实现绳子的模拟,之后一步一步推导布料仿真上去。
从绳子推导到布料的仿真:
布料本质上就是一系列的绳子的集合,那么可以通过不同绳子的组合来模拟布料。
附录
【1】百科百科。https://baike.baidu.com/item/%E8%83%A1%E5%85%8B%E5%AE%9A%E5%BE%8B/2307271?fr=aladdin
站在巨人的肩上。
创作不易,如果喜欢的话,请点赞,收藏,谢谢。
内容本周末再填写,可以先移步git项目
这篇关于Unity 布料仿真笔记1 弹簧质点模型的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







