本文主要是介绍Gaussian Temporal Awareness Networks GTAN论文阅读笔记,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
论文地址:Long_Gaussian_Temporal_Awareness_Networks_for_Action_Localization_CVPR_2019_paper.pdf
概述
基于图像帧的 TAL 的常规方法步骤为:通过 1D 的时序通道卷积来获得更大的感受野,然后在此基础上预测动作类别和时序边界。这种方法获得的 proposal 被分配了相同的感受野,然而不同的动作的时序长度是不同的。为了解决这个问题,2019 年,F. Long 等人提出了 GTAN(Gaussian Temporal Awareness Networks),对每一个 proposal,通过学习一个高斯核来表达时序信息。
首先网络提供通过 3D-CNN 提取特征,并通过 2 个 1D 卷积加上 1 个 1D 池化操作增加感受
野。随后采用 8 个 1D 的卷积来在不同的时序尺度上生成多个 feature map,类似于目标检测中的FPN。在每个 feature map 上,学习一个高斯核来描述一个动作的时序长度,高重合度的高斯核将会被合并,最后再使用 Gaussian Pooling 整合特征。
网络结构

输入一个视频,通过3D卷积网络提取clip-level的特征。然后经过两个时序卷积和一个max-pooling进一步增加感受野。常规的one-stage时序行为定位的方法是采用1D卷积生成proposal用来识别和边界回归。这种方法获得的action proposal被分配了相同的感受野。然而不同的action的时序长度是不同的。
为了解决这个问题,本文提出了高斯核学习:为每个cell生成一个高斯核。具体来说,我们定义 feature map为 { f i } i = 0 T j − 1 ∈ R T j × D j \left\{f_{i}\right\}_{i=0}^{T^{j}-1} \in \mathbb{R}^{T^{j} \times D^{j}} {fi}i=0Tj−1∈RTj×Dj ,其中 T j T^{j} Tj 和 D j D^{j} Dj 为时序长度和特征维度。对于一个 proposal P t j P_{t}^{j} Ptj ,中间位置为 t t t ,通过一个高斯核 G t j G_{t}^{j} Gtj 来刻画他的时序尺度。通过一个1D 卷积层来学习标准差 σ t j , G t j \sigma_{t}^{j}, G_{t}^{j} σtj,Gtj 可定义如下:
W t j [ i ] = 1 Z exp ( − ( p i − μ t ) 2 2 σ t j 2 ) s.t. p i = i T j , μ t = t T j i ∈ { 0 , 1 , … , T j − 1 } , t ∈ { 0 , 1 , … , T j − 1 } \begin{gathered} W_{t}^{j}[i]=\frac{1}{Z} \exp \left(-\frac{\left(p_{i}-\mu_{t}\right)^{2}}{2 \sigma_{t}^{j^{2}}}\right) \\ \text { s.t. } p_{i}=\frac{i}{T^{j}}, \mu_{t}=\frac{t}{T^{j}} \\ i \in\left\{0,1, \ldots, T^{j}-1\right\}, t \in\left\{0,1, \ldots, T^{j}-1\right\} \end{gathered} Wtj[i]=Z1exp(−2σtj2(pi−μt)2) s.t. pi=Tji,μt=Tjti∈{0,1,…,Tj−1},t∈{0,1,…,Tj−1}
其中, Z Z Z 为标准化常量。然后我们可以通过 σ t j \sigma_{t}^{j} σtj 来获得时序边界: a c = ( t + 0.5 ) / T j , a w = r d ⋅ 2 σ t j / T j a_{c}=(t+0.5) / T^{j}, \quad a_{w}=r_{d} \cdot 2 \sigma_{t}^{j} / T^{j} ac=(t+0.5)/Tj,aw=rd⋅2σtj/Tj,其中 a c a_{c} ac 和 a w a_{w} aw 为时序边界的中心和宽度。

如上图所示,当两个高斯核的重合度IOU=H/L大于threshold时,需要将其合并,新合并的高斯核如下:
W [ i ] = 1 Z exp ( − ( p i − μ ′ ) 2 2 σ ′ 2 ) s.t. p i = i T , μ ′ = t 1 + t 2 2 ⋅ T , σ ′ = L 2 i ∈ { 0 , 1 , … , T − 1 } \begin{aligned} W[i] &=\frac{1}{Z} \exp \left(-\frac{\left(p_{i}-\mu^{\prime}\right)^{2}}{2 \sigma^{\prime 2}}\right) \\ \text { s.t. } \quad p_{i} &=\frac{i}{T}, \quad \mu^{\prime}=\frac{t_{1}+t_{2}}{2 \cdot T}, \quad \sigma^{\prime}=\frac{L}{2} \\ i & \in\{0,1, \ldots, T-1\} \end{aligned} W[i] s.t. pii=Z1exp(−2σ′2(pi−μ′)2)=Ti,μ′=2⋅Tt1+t2,σ′=2L∈{0,1,…,T−1}
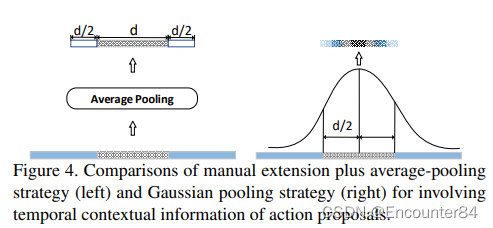
相比常规的Average Pooling(左),Gaussian Pooling考虑到了时序的上下文信息。具体的Gaussian pooling如下,其中 F t j F_{t}^{j} Ftj 被用于后续的行为识别和时序边界回归。
F t j = 1 T j ∑ i = 0 T j − 1 W t j [ i ] ⋅ f i F_{t}^{j}=\frac{1}{T^{j}} \sum_{i=0}^{T^{j}-1} W_{t}^{j}[i] \cdot f_{i} Ftj=Tj1i=0∑Tj−1Wtj[i]⋅fi
损失函数
GTAN网络一共有三个loss函数,分别对应分类,定位和重合度。
L c l s = − ∑ n = 0 I n = c log ( y n a ) L l o c = S L 1 ( φ c − g c ) + S L 1 ( φ w − g w ) L o v = ( y o v − g i o u ) 2 \begin{aligned} &L_{c l s}=-\sum_{n=0} I_{n=c} \log \left(y_{n}^{a}\right) \\ &L_{l o c}=S_{L 1}\left(\varphi_{c}-g_{c}\right)+S_{L 1}\left(\varphi_{w}-g_{w}\right) \\ &L_{o v}=\left(y_{o v}-g_{i o u}\right)^{2} \end{aligned} Lcls=−n=0∑In=clog(yna)Lloc=SL1(φc−gc)+SL1(φw−gw)Lov=(yov−giou)2
最后的loss函数是三个loss的加权和:
L = L c l s + β L l o c + γ L o v L=L_{c l s}+\beta L_{l o c}+\gamma L_{o v} L=Lcls+βLloc+γLov
参考:https://zhuanlan.zhihu.com/p/73674552
这篇关于Gaussian Temporal Awareness Networks GTAN论文阅读笔记的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







