代码随想录算法训练营第四十二天【动态规划part04】

本文主要是介绍代码随想录算法训练营第四十二天【动态规划part04】 | 01背包、416. 分割等和子集，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

01背包问题

题目链接：

题目页面

求解思路：

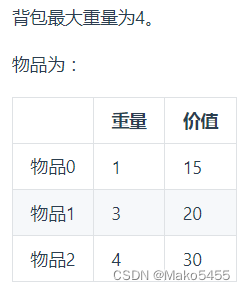
确定dp数组及其下标含义：dp[i][j] 表示从下标为 [0] 到 [i] 的物品里任意选取，放进容量为j的背包，此时的价值总和最大值
确定递推公式：
不放物品i，总和为dp[i-1][j]；
放物品i，总和为 dp[i - 1][j - weight[i]] + value[i]；
因此递推公式为 dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
dp数组的初始化：注意第一行，dp[0][j]，即i为0，存放编号0的物品的时候。当 j < weight[0]的时候，dp[0][j] 应该是 0，因为背包容量比编号0的物品重量还小；当j >= weight[0]时，dp[0][j] 应该是value[0]，因为背包容量放足够放编号0物品
确定遍历顺序：有两个遍历的维度，分别为物品与背包重量，本题中先遍历哪个都可以
举例推导dp数组：如图所示

代码：

#include <bits/stdc++.h>
using namespace std;int n, bagweight;
void solve(){vector<int> weight(n, 0); // 每件物品所占空间vector<int> value(n, 0); // 每件物品的价值for (int i = 0; i < n; i++){cin >> weight[i];}for (int j = 0; j < n; j++){cin >> value[j];}// 先将dp数组全部初始化为0vector<vector<int>> dp(weight.size(), vector<int>(bagweight + 1, 0));// 当只有1件物品的时候（第一行）的初始化for (int j = weight[0]; j <= bagweight; j++){dp[0][j] = value[0];}// 开始遍历for (int i = 1; i < weight.size(); i++){ // 遍历物品for (int j = 0; j <= bagweight; j++){ // 遍历背包if (j < weight[i]) // 放不下的情况dp[i][j] = dp[i-1][j];else dp[i][j] = max(dp[i-1][j], dp[i-1][j-weight[i]] + value[i]);}}cout << dp[weight.size()-1][bagweight] << endl;
}int main(){cin >> n >> bagweight;solve();return 0;
}

01背包问题（滚动数组）

题目链接：

卡码网KamaCoder

求解思路：

对于背包问题其实状态都是可以压缩的。

在使用二维数组的时候，递推公式：dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);

其实可以发现如果把dp[i - 1]那一层拷贝到dp[i]上，表达式完全可以是：dp[i][j] = max(dp[i][j], dp[i][j - weight[i]] + value[i]);

与其把dp[i - 1]这一层拷贝到dp[i]上，不如只用一个一维数组了，只用dp[j]（一维数组，也可以理解是一个滚动数组）。

这就是滚动数组的由来，需要满足的条件是上一层可以重复利用，直接拷贝到当前层。

动规五部曲

确定dp数组的意义：dp[j] 表示容量为j的背包，所背的物品最大价值为 dp[j]
确定递推公式：根据上文可知，dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
dp数组的初始化：因为背包容量为0所背的物品的最大价值就是0，所以dp[0] = 0；dp[j] 在计算的时候会加上自身来判断更大的值，且所有物品价值大于0，为了让值不被初始值覆盖，其他下标也都初始化成0
遍历顺序：注意必须倒序遍历，并且先遍历物品再遍历背包。
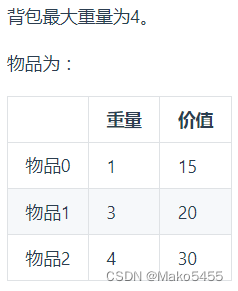
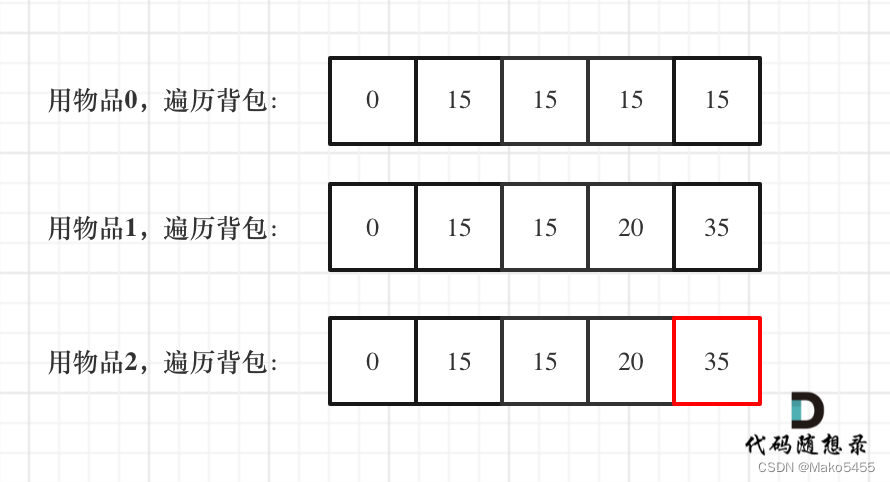
举例推导dp数组：如图所示

代码：

#include <iostream>
#include <vector>
using namespace std;int main(){int M, N;cin >> M >> N;vector<int> costs(M);vector<int> values(M);for (int i = 0; i < M; i++)cin >> costs[i];for (int i = 0; i < M; i++)cin >> values[i];vector<int> dp(N+1, 0);for (int i = 0; i < M; i++){for (int j = N; j >= costs[i]; j--){dp[j] = max(dp[j], dp[j-costs[i]] + values[i]);}}cout << dp[N] << endl;return 0;
}

416. 分割等和子集

题目链接：

力扣（LeetCode）官网 - 全球极客挚爱的技术成长平台

求解思路：

分割成两个等和子集，等于找出和为一半的子集，等于一个容量为数组和一半的背包可以被数组里的数装满。

注意事项

背包的体积为sum / 2
背包要放入的商品（集合里的元素）重量为元素的数值，价值也为元素的数值
背包如果正好装满，说明找到了总和为 sum / 2 的子集。
背包中每一个元素是不可重复放入。

动规五部曲

确定dp数组及其下标含义：dp[j] 表示背包总容量为j，放进物品后，背包的最大重量为dp[j]
确定递推公式：因为物品i的重量和价值都是nums[i]，所以 dp[j] = max(dp[j], dp[j - nums[i]] + nums[i]);
dp数组的初始化：dp[0] = 0，其他下标也为0（因为价值都是正数）
遍历顺序：先物品，再背包，并且背包要倒序遍历（参考前面滚动数组）
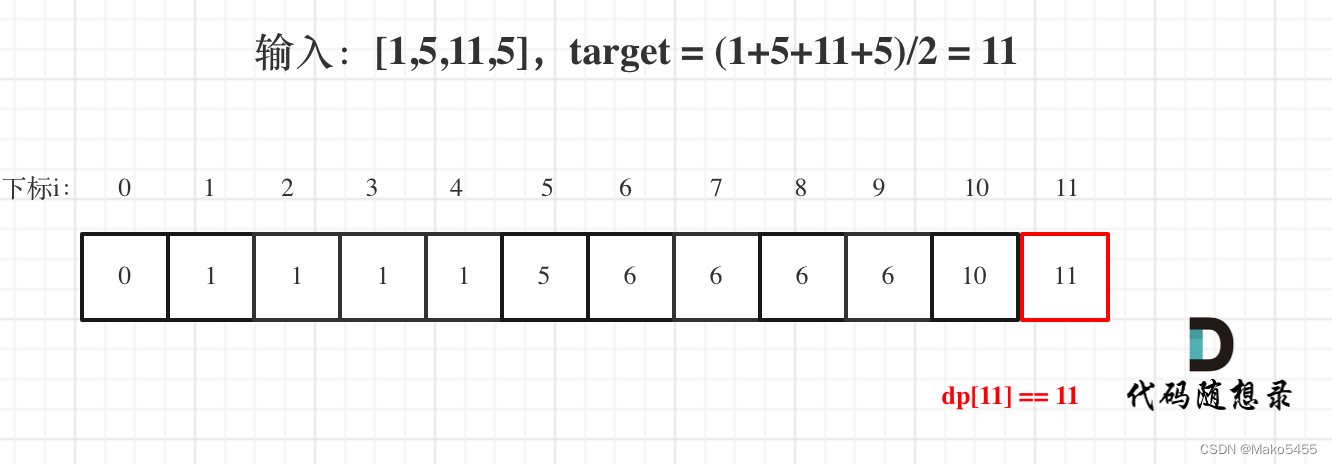
举例推导dp数组：以[1,5,11,5]为例，如图

代码：

class Solution {
public:bool canPartition(vector<int>& nums) {// 求和int sum = 0;for (int i : nums) sum+= i;// 和为奇数不可能有解if (sum % 2 == 1) return false;// 01背包int target = sum / 2;vector<int> dp(target+1, 0);for (int i = 0; i < nums.size(); i++){for (int j = target; j >= nums[i]; j--){dp[j] = max(dp[j], dp[j-nums[i]] + nums[i]);if (dp[j] == target) return true;}}return false;}
};

这篇关于代码随想录算法训练营第四十二天【动态规划part04】 | 01背包、416. 分割等和子集的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！