一种融合偶然和认知不确定性的贝叶斯深度学习RUL框架

_原文： _《《A Bayesian Deep Learning RUL Framework Integrating Epistemic and Aleatoric Uncertainties》

_作者__： _Gaoyang Lia，Li Yangb，Chi-Guhn Leec，Xiaohua Wangd，Mingzhe Ronge

_作者单位： _

_a. School of Electrical Engineering, State Key Laboratory of Electrical Insulation and Power Equipment, Xi’an Jiaotong University
_

b. Big Date Center of State Grid Corporation of China, Beijing, China

c. School of Reliability and Systems Engineering, Beihang University

d. Beijing, China，Department of Mechanical and Industrial Engineering

e. University of Toronto, Toronto, ON, Canada

_期刊名称__： _IEEE Transactions on Industrial Electronics

引用格式__：Li G, Yang L, Wang X H, et al. A Bayesian Deep Learning RUL Framework Integrating Epistemic and Aleatoric Uncertainties[J]. IEEE Transactions on Industrial Electronics, 2021, 68(9):8829-8841

在线链接：https://ieeexplore.ieee.org/document/9145803

图文素材：张祥浩

排版整理：****王金威

指导审核****：杨乐昌

注：本文章已提供完整版中文翻译，如需英文文献及翻译文档，请参见底部阅读原文

摘 要

近年来，深度学习 (DL) 在预测和健康管理领域取得了显着进步。然而，大多数DL方法并未解决工业设备中广泛存在的预后不确定性问题。本文提出了一种新颖的贝叶斯深度学习 (BDL) 框架来表征预后不确定性。该框架的一个显着优势是其能够捕获两个关键不确定性的综合影响: 1) 认知不确定性，解释模型中的不确定性; 2) 代表随机干扰 (例如测量误差) 的影响的预测不确定性。前者源于模型权重的可变性，后者的特征在于选定的寿命分布。我们通过将BDL定义为生命周期参数的先验来整合这两个不确定性。执行顺序贝叶斯增强算法以提高估计精度并压缩可信区间。从断路器的液压机构收集的真实数据集验证了我们框架的卓越预测性能。

01

简 介

随着传感器技术的快速发展，各种工业设备可以在线监测健康状况，为预测和健康管理 (PHM) 技术提供足够的数据支持[1]。

作为PHM的重要组成部分，预后提供有关未来退化趋势和剩余使用寿命 (RUL) 的最新信息，从而促进基于成本效益和安全关键条件的维护计划[2]。

基本上，预后方法可以分为模型驱动和数据驱动方法。基于模型的方法在很大程度上依赖于对退化机制和进化规律的全面理解[3]。这通常受到故障机制和操作环境的复杂性的限制。另一方面，数据驱动的方法主要需要数据大小/质量，并且很少受特定模型结构的限制。一种代表性的数据驱动方法是深度学习 (DL)，由于其处理复杂的非线性数据结构的能力[4],[5]，它引起了极大的关注。最近，各种DL结构，如RBM[6]、RNN[7],[8]和CNN[9],[10]已成功应用于RUL预测。

尽管基于DL的预后技术取得了进步，但大多数相关工作仅提供确定性的RUL值，无法捕获预后的不确定性[5]。

这在现实世界的PHM应用中显然是不够的。一方面，由于诸如噪声污染，测量误差和传感器技术的其他限制等不可控制的因素，传感器测量不可避免地面临着极大的不确定性[11]。另一方面，可访问的监视数据的限制导致对模型可信度的不确定，这被称为认知不确定性。贝叶斯是不确定性量化的强大框架，它利用后验假设推理来增强泛化和量化DL预测的可信水平[12]。特别地，贝叶斯神经网络 (BNNs) 已经作为一个强大的框架出现，用于对复杂的DNN进行不确定性建模和过度拟合缓解[13]。然而，在现有的BNN模型中仍然没有解决三个基本的挑战[14]: 1) 缺乏整合这两个不确定性的系统框架，2) 在处理复杂的非线性模型和非共轭分布时，通常会忽略或简单地用常数高斯来表征，而忽略了预后的异方差性; 3) 在处理复杂的非线性模型和非共轭分布时，后验推理是相当棘手的。

本文通过构建一个贝叶斯深度学习 (BDL) 框架来解决这些挑战，该框架将认知不确定性和先验不确定性整合到非线性模型结构中。据我们所知，这是首次尝试量化DL框架中两种不确定性的综合影响，从而更好地揭示了资产健康状况的演变模式。为此，提出了一种新的不确定性分解算法，以明确可信区间(CI)的组成。值得注意的是，此框架中的相关不确定性取决于数据，而不仅限于高斯。这与[15] 不同，后者仅专注于认知不确定性分析，而没有解决异方差噪声的不可忽略的影响。我们框架的另一个显着优势是，它允许使用缺失数据进行不确定性估计。这对于具有相对较长的使用寿命 (例如，高压断路器) 或较短的使用周期的工业设备非常有用，这两者都提供了有限的故障运行数据。

最后，我们提出了一种序列贝叶斯提升算法来提高BDL的性能。其关键思想是建立多步RUL预测之间的长期依赖性，并通过贝叶斯推理更新后验RUL。该算法的优势在于: 1) 充分利用不同测量下的历史RUL信息来提高性能; 2) 预测和更新步骤都可以在单个BDL内执行，大大降低了预测复杂度。

第二节介绍了相关理论。第三节介绍了贝叶斯不确定性理论的基本框架。第四节讨论BDL驱动的预后过程。第五节分析了验证平台。第六节讨论了我们的建议的有效性。第七节是本文的结束语。

02

相关工作

认知不确定性和任意不确定性可以被认为是对模型参数或输出的先验。

2.1

基于模型和混合方法中的不确定性

随机过程是描述预测不确定性的常见模型驱动方法[3]。然而，大多数相关工作假设的模型参数是确定的，这只能捕捉到任意的不确定性。基于Wiener的方法的最新进展试图通过假设漂移参数的随机性和设置先验分布来引入认知不确定性。例如：Si等人[16]假设自适应漂移中有高斯噪声。Zhai等人[17]将漂移参数视为布朗运动，由Li等人进一步扩展[18]。但是，假设退化遵循某种预先设定的路径可能会限制它们的应用。为了解决这个问题，一些混合方法将数据驱动技术与基于模型的方法相结合，通过用数据驱动方法代替状态转换模型或测量模型[19]。然而，它们的参数通常是超参数。只有少数工作尝试使用真实数据来应对噪声预测中的挑战[20]。

2.2

深度学习与贝叶斯神经网络

DL已被证明在处理高度非线性和变化的传感器数据方面是有效的[4]。一个有代表性的应用是Liao等人进行的高维特征提取，其中提出了一种改进的RBMT来自动生成特征[6]。类似地，Ellefse等人[7]在发动机退化分析中应用了半存储长短期记忆(LSTM)网络。另一个应用是直接RUL学习。Zhao等人提出了一种局部特征GRU来实现机器健康监测[8]。Yang等应用了双阶段-CNN进行RUL估计，而无需对任何特征提取器进行反求[10]。但是，这些工作仅研究了RUL的确定性形式，而没有解决RUL的概率性。为了填补这一空白，一些文献试图整合外部集成方法[20]，[21]来估计不确定性。然而，这种方法的计算开销很大。

与DL框架不同，BNN是一种完全贝叶斯方法，通过将DNN的确定性权重替换为分布。尽管BNN的结构易于公式化，但相应的参数很难估计。早期的研究依赖于近似，例如拉普拉斯近似、蒙特卡罗马尔可夫链 (MCMC) 和变分推断[13]。在DL的工具库中，Blundell等人通过将反向传播（Backprop）方法引入贝叶斯实现DL中的变分推理，在此基础上提出了各种新技术[22]。Gal等人在近似贝叶斯推理中开发了一个随机丢弃（dropout）框架[23]。Peng等人应用BNN来量化全生命周期预后中的认知随机性[15]。但是，未解决相关影响以及不确定性整合和分解方法，也未捕获预后结果之间的内在依赖性以提高准确性。

03

不确定度分析

本部分研究了广泛存在于预测问题中的两种不确定性来源，并构建了不确定性集成与分析的贝叶斯框架。

3.1

不确定性来源

由于数据和技术的限制，现实世界的预后问题 (数据或模型驱动) 不可避免地面临两种类型的不确定性: 反映数据收集和传输中的噪声污染的偶然不确定性和反映模型属性的认知不确定性。

图1中引入了一个综合两种不确定性的说明性回归模型。模型_y=ax+b_由未知系数a和b来拟合训练集 [X,Y]。由于可访问训练数据的限制 (例如，部分观测值，有限的采样率)，a和b的估计值会不可避免地会偏离真实值。这种推导可以用概率分布_p(a,b|X,Y)来表征。这种不确定性来自模型参数，被称为认知不确定性。另一方面，即使具有极其丰富的数据，数据收集和测量通常也会受到随机噪声 (例如测量误差) 的污染，其特征可以是_p(y|x,a,b)=p(ax+b,σ)，其中 σ 是噪声项。这种随机干扰被称为偶然不确定性。这两个不确定性共同导致预后与实际结果之间的差异。

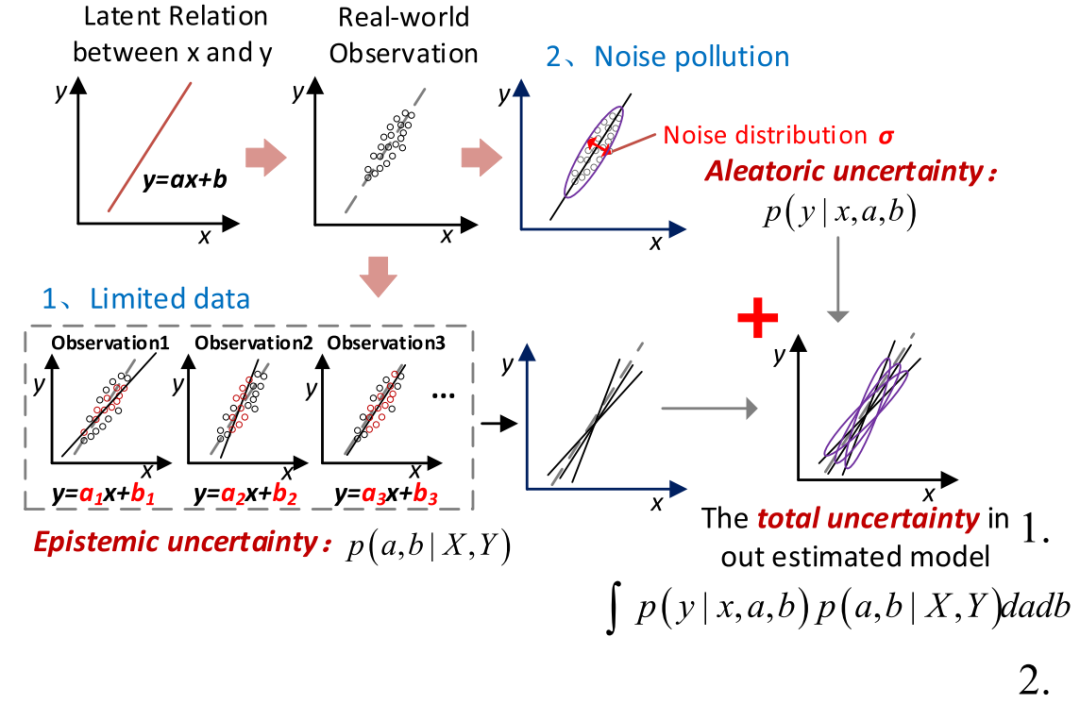
图1 不确定性来源

3.2

贝叶斯驱动的不确定性积分

考虑由系数集Θ与历史数据集[X,Y]参数化的一般回归函数f(.)。这里，X和Y分别表示自变量和因变量。与图1一致，认知不确定性形成与系数集 Θ的可变性，由条件概率分布_p(Θ|X,Y)反映。通过引入先验_p(Θ)，可以在贝叶斯框架[12]下有效地量化这种不确定性:

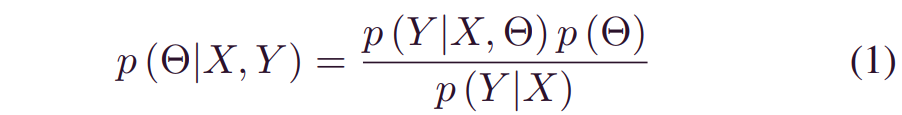
其中_p(Θ)_ 表示关于未知模型参数的先验信念。通过 [X,Y] 进行训练，可以将_p(Θ)_ 修改为具有较窄分布间隔的后验_p(Θ|X,Y)_。

此外，偶然不确定性通过概率结构_p(y|x,Θ)_ 立即影响预测结果y。然后，可以通过以下积分方程将两个不确定性有效地合并到单个贝叶斯框架中：

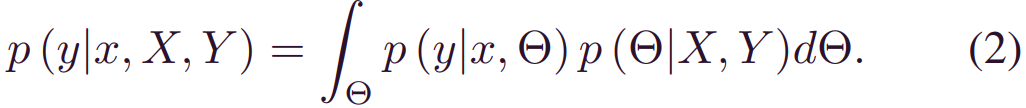
式(2)反映了应用于新样本x时预测结果y的预测不确定性。可以得出两个关键结论：1)积分可以实现全局数据利用率 (通过历史[X,Y])和预测更新(在新的观察x上)，以及2) 人工引入的参数不确定性_p(Θ|X,Y)_通过积分进行集成。这种积分也可以通过方差累积理论来解释。设预测方差_Var(y)_代表总预后不确定性。然后，_p(Θ|X,Y)_和_p(y|x,Θ)_对_Var(y)_的贡献可以构造为：

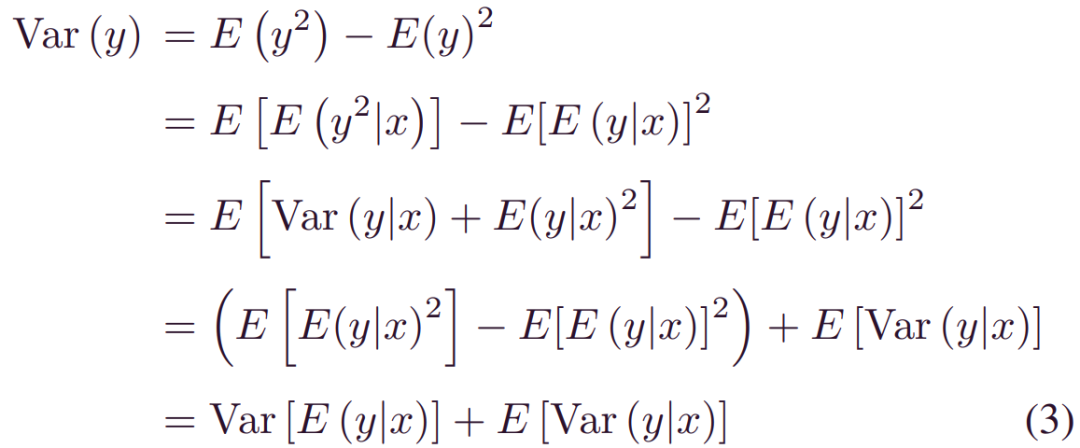
其中_Var[E(y|x)]_是变量期望的方差。这也称为总方差定律[24]。期望值_E(y|x)_由于模型参数的可变性而波动，该模型参数衡量了认知不确定性的影响。相反，通过在_E[Var(y|x)]_中取平均值来消除模型参数的可变性，其中提取了由于随机噪声引起的平均效应。总而言之，认知方差_Var[E(y|x)]_和偶然方差_E[Var(y|x)]_共同有助于预后方差，这与(2)一致。

备注1：上述贝叶斯框架通过1) 在预测分布中学习和集成这两个不确定性，以及2) 分解它们对预测方差的影响来捕获认知和任意不确定性。此外，该贝叶斯统计框架可以在理论上显着增强模型的泛化。然而，其在现实预后中的应用面临以下挑战：

  1)方程 (1) 的后验推论可能非常棘手，仅适用于一些简单的线性回归和具有高斯噪声的共轭分布。  2) 为了简化计算，通常假定任意不确定度为常数，这与实际测量数据越多，任意不确定度越小的趋势相矛盾。 

04

贝叶斯深度学习(BDL)框架

本节通过将贝叶斯统计框架扩展到贝叶斯深度学习(BDL)来解决上述挑战。首先，用一个DNN来表征预测模型，该DNN通过概率权值来表征认知不确定性。其次，将预测分布_p(y|x,Θ)_扩展到更一般的数据驱动和非高斯场景。 最后，提出了一种用于性能提升的结果贝叶斯融合算法。图2以图形方式说明了BDL驱动的预测过程。与一般的BNNs[15]相比，所提出的框架引入了一个模拟层来弥合模型参数不确定性 (认知) 和噪声诱导不确定性 (偶然)。一方面，相关节点是概率的，具体取决于输入和概率权重。另一方面，它们还定义了描述平均噪声的概率寿命分布。因此，这两个不确定性可以在预测过程中综合考虑。然后，通过变分推理执行BDL权重的后验推理，并据此提出了一种不确定性分解算法。最后，利用多步BDL预测之间的时间序列依赖性，提出了一种序列贝叶斯提升算法来提高预测性能。

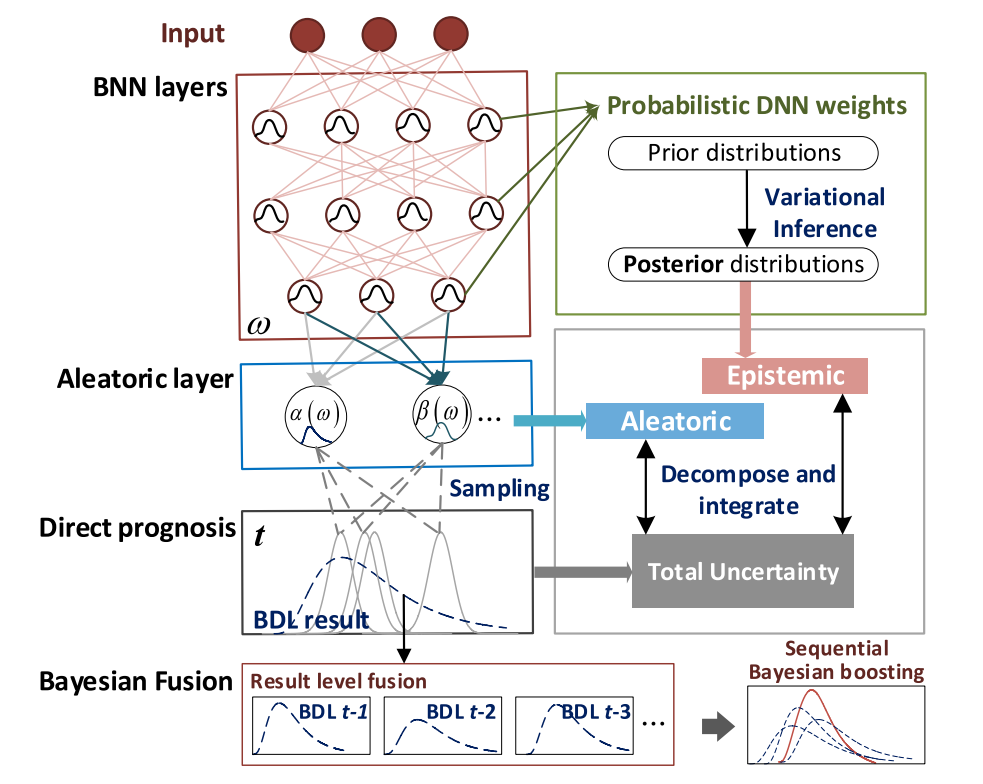
图2 BDL的总体预测框架

4.1

基本结构

在 (1)-(3) 之后，构建的BDL模型用表示认知不确定性的概率权重代替确定性权重ω，并引入定义特定寿命分布的认知层，来描述与数据相关的噪声。例如，考虑一个由α,β参数化的双参数寿命分布。然后，将(2)中的_p(y|x,Θ_)变换为：

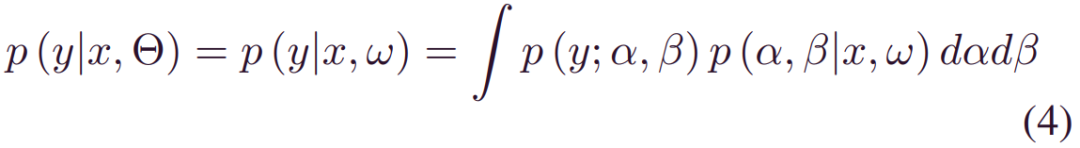
其中ω表示随机模型权重。当监测数据X和相应的标签(RULs) Y可用时，后验_p(w|X,Y)_可以从(1)推断为：

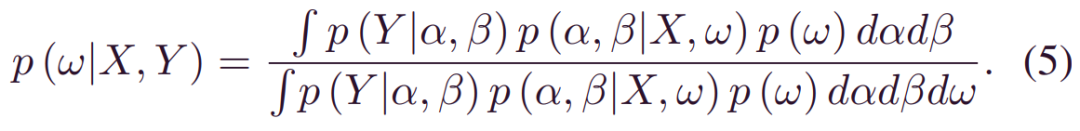
之后，（2）中的预测的分布可以重写为：

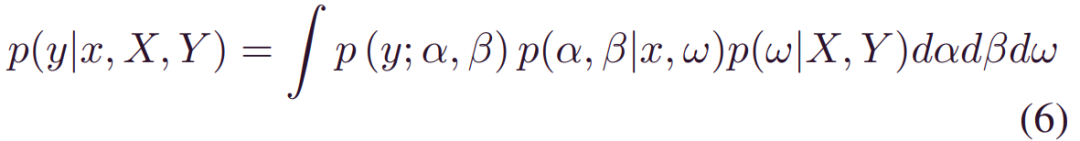
其中：

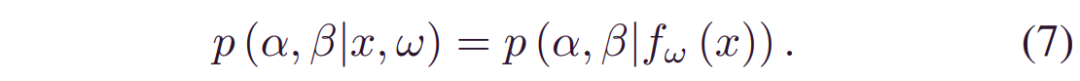
备注2：该框架为不确定性量化赋予了很强的灵活性。值得注意的是，可以通过任意分布(例如Weibull) 来表征偶然分布_p(y;α,β)_。此外，由于_p(α,β|x,w)_取决于x，因此预测的RUL分布是数据决定的。下面，我们将详细介绍BDL驱动的预后，重点讨论三个关键问题:（5）中的后验推断，(6)中的预后和（3）中的不确定性量化。

4.2

训练与分解

值得注意的是，由于DNN中的巨大参数量，非共轭先验和非线性激活，(5) 中的_p(w|X,Y)_的封闭形式是难以处理的。然而，随机变分推理的最新进展[25]为近似推理提供了有用的工具。核心思想是通过一个由θ参数化的新分布_qθ(w)来近似实后验_p(w|X,Y)。与_p(w|X,Y)_不同，_qθ(w)_可以通过封闭形式分配，从而降低了推断的难度。Kullback-Leibler (KL) 散度[26]是两个分布之间距离的常见度量。_qθ(w)_和_p(w|X,Y)_之间的KL散度定义为：

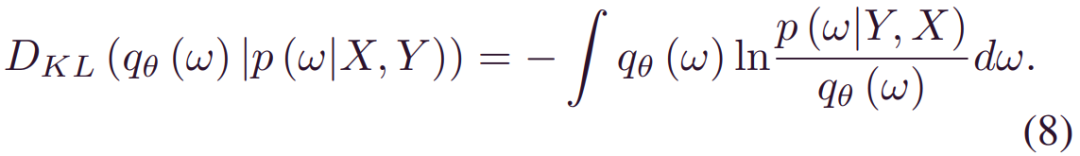
因此，如果我们可以找到使_DKL(qθ(w)|p(w|X,Y))最小化的_q~θ(w)， 则(6)中的预测分布可以近似为：

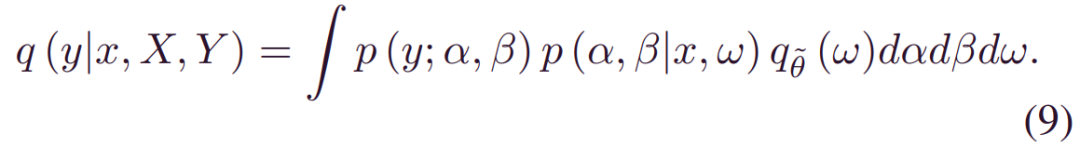
接下来，我们导出最小化(8)的等价形式。请注意，以下公式在方差推断中成立：

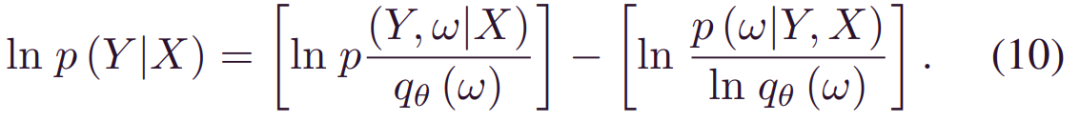
取_qθ(w)_条件期望得到：

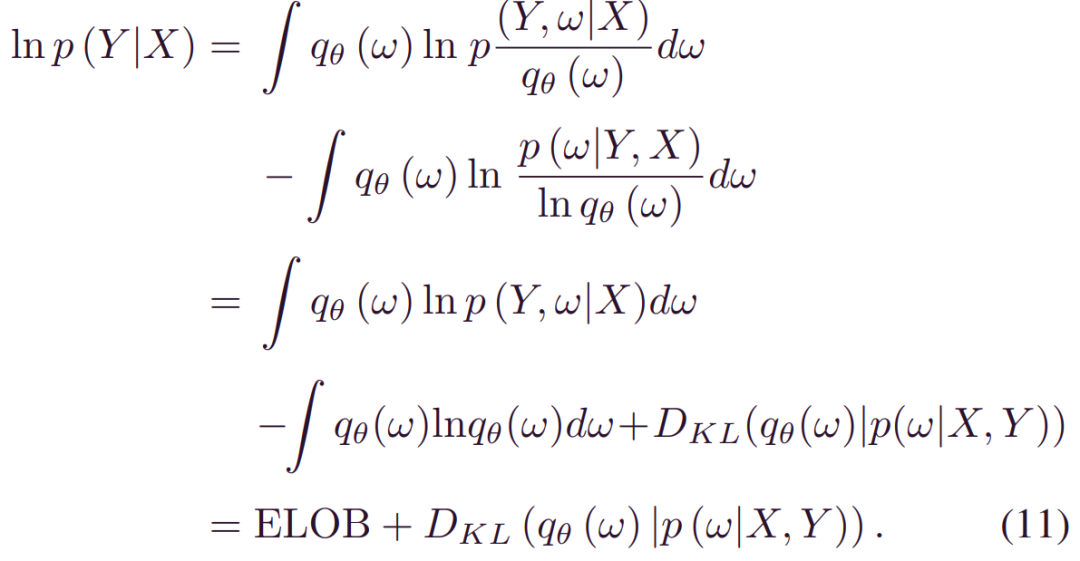
_lnp(Y|X)_是一个常数,最小化_DKL(qθ(w)|p(w|X,Y))_等价于最大化（11）中的第一部分，被称为证据下限（ELOB），ELOB也等价于：

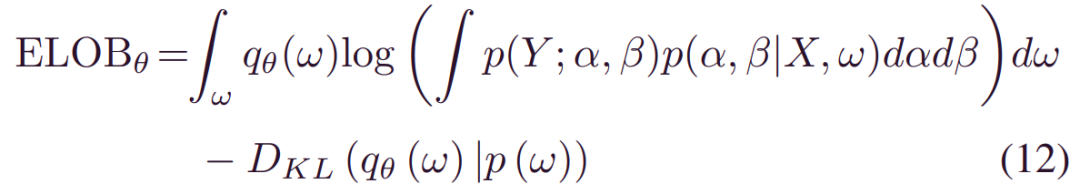
其中，第一项表示_qθ(w)_上对数似然的期望，第二项表示近似_qθ(w)_和先验_p(ω)_之间的KL散度。总之，如果找到最优解θ_{最大化_ELOBθ_，_q}θ(w)_可用于认知不确定性量化。

尽管ELOB中对_qθ(w)_的分析期望是棘手的，但可以通过蒙特卡洛(MC)积分获得其无偏估计。然后，(12)中的第一项变为：

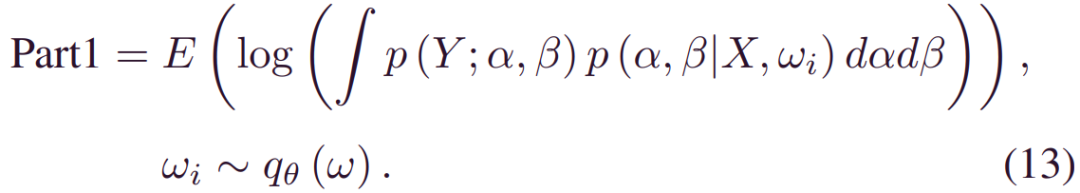
由于α,β的可变性来自模型权重，因此_p(Y;α,β) p(α,β|X,wi)_也可以简化为_p(Y;α(X,wi),β(X,wi))_因此：

(12) 中的第二项可以通过假设来简化: 1)w的先验是高斯分布：

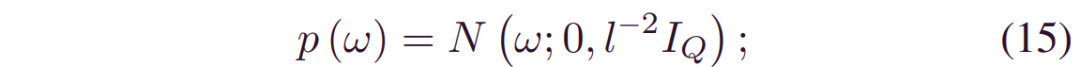
其中l是长度标度，IQ是具有Q维数的单位矩阵，Q是模型权重的数量2) (12) 中的_qθ(w)_遵循高斯混合分布：

其中_pd_是混合概率，k2_是一个小方差。关于这两个假设的有效性和合理性的更多细节可以在[23] 中找到。然后，(12) 中的第二项变成了高斯和单个高斯之间的差异。根据[23]，这样的具有大节点数和小_k2(在实践中通常是正确的)的KL发散可以近似为：

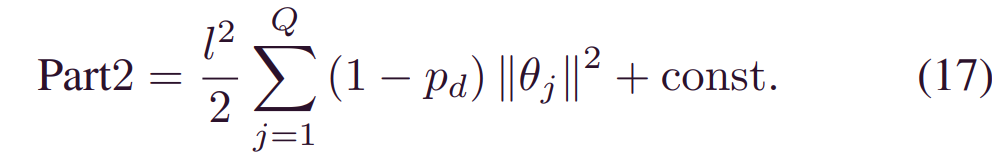
因此，(12) 中的_ELOBθ_被转换为：

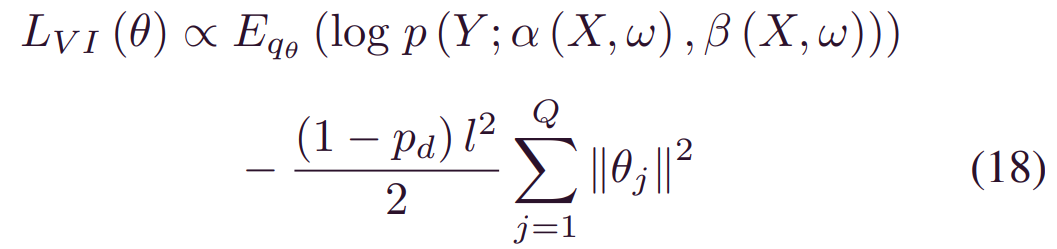
其中w~qθ(w)。在n个训练样本的情况下，最大化 (12) 中的_ELOBθ_等于最小化以下损失函数:

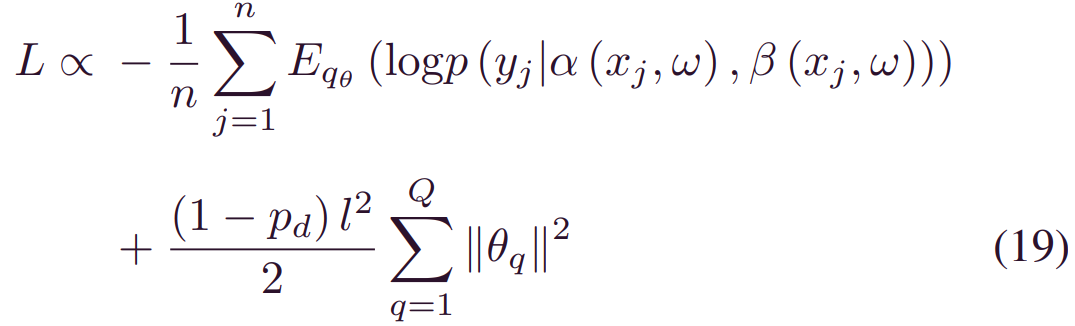
其中w~qθ(w)。这样，最小化 (8) 被成功地转换为 (19) 中定义的损失最小化问题。值得注意的是，由于_qθ(w)_服从混合高斯分布时，因此存在一种从分布_qθ(w)_进行采样的实用方法，即在权重相乘之前执行dropout[27]。换句话说，在训练过程中，权重由概率_pd_控制，训练过程中有两种选择: 1)从_N(0,k2I)_采样时被丢弃，2)从_N(θj,k2I)采样时接近_θj。因此，dropout法训练可以应用于最小化(19)的损失函数。

经过训练，我们可以通过蒙托卡罗(MC)抽样得到(3)中的预测方差为：

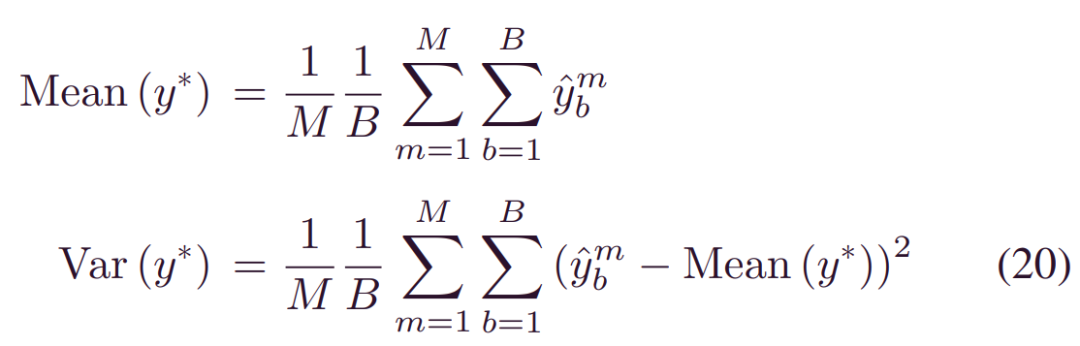
通过依次绘制_αm(xi,wi),βm(xi,wi)与_w^{m_~_qθ(w)_，_y}bm~p(yi|αm,βm)，其中1≤m≤M和1≤b≤B。这双重采样过程归因于特定的贝叶斯结构。然后，根据任意方差的定义，通过提取每个模型权重的平均方差，推导出任意方差_E[Var(y|x)]_：

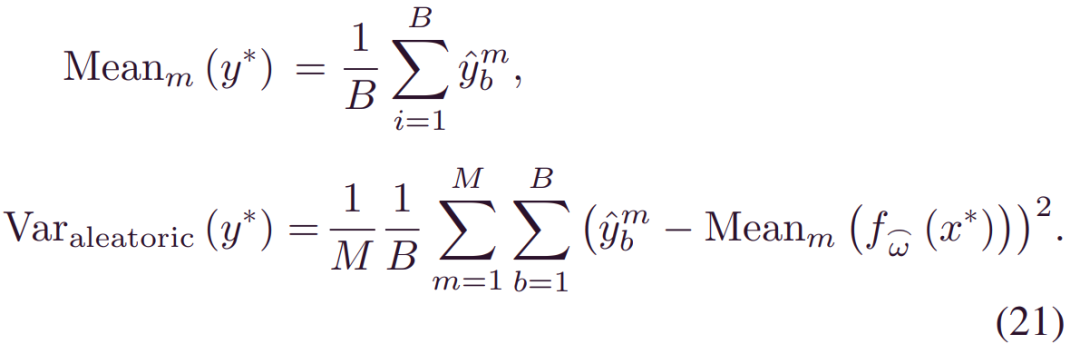
因此，通过从总方差中消除认知方差，可以从（4）推断认知方差：

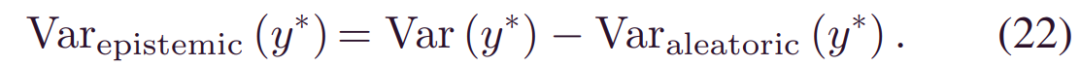
算法1中引入了不确定性分解。

该框架的显着优势在于其在适应各种DNN结构方面的灵活性。在本文中，选择GRU[28]是因为它提供了与LSTM相似的性能，但在计算上更便宜。

算法1

4.3

寿命分布与激活函数

(19)中损失函数要求参数化_p(y;α(x,w),β(x,w))_。在这里，我们介绍了一种灵活的量化方法，它允许使用删失数据，这是有用的，因为高质量的运行到故障数据通常在实际健康监测中受到限制，因为维护干扰，丢失到后续或使用结束等原因。

采用广泛使用的右截尾数据[29]用于量化。基于完整故障数据的量化可以看作是一个特例，此处省略。 让Ci表示截尾时间。然后，观察到的数据的终点是运行时间Ti和截尾时间Ci的最小值，即：

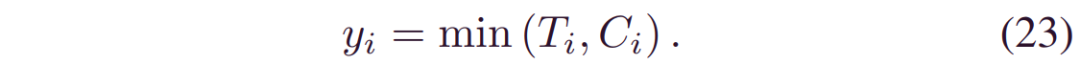
相应地，(19) 中的第一部分成为以下具有寿命分布f的负对数似然函数:

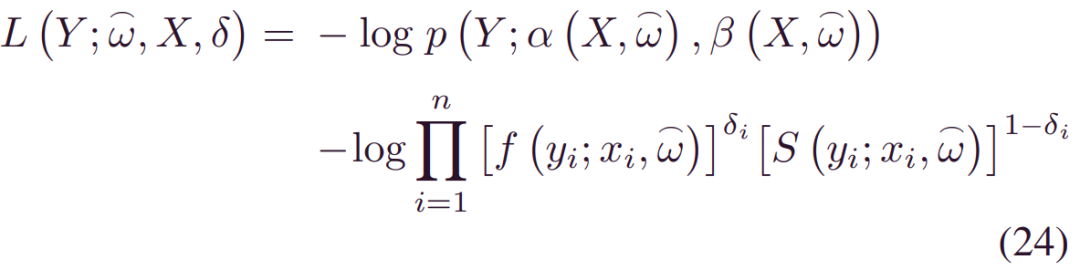
其中_S(yi;xi,w^{)=1-∫0yif(τ;xi,w})}dτ_是生存函数，n是样本数，δi是给出的指标：

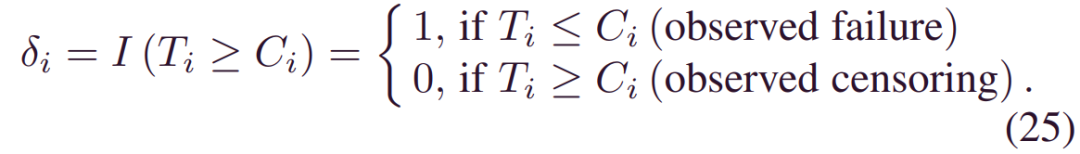
尽管_p(y|α,β)_可以通过任意分布来表征，但那些产生(24)封闭形式的分布可以促进梯度下降的实现。本节的其余部分介绍了三种可行的分布。

Gaussian BDL：高斯在寿命分析中表现出很好的特性。其对应的密度为：

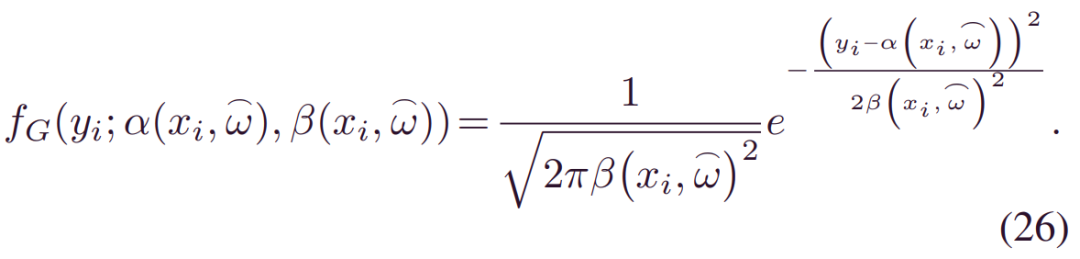
将 (26) 代入 (24) 和 (19) 得到高斯BDL。

Weibull BDL：Weibull被广泛应用于生存分析，简单但富有表现力[30]。一个由_α(xi,wi)_和_β(xi,wi)_参数化的Weibull分布是：

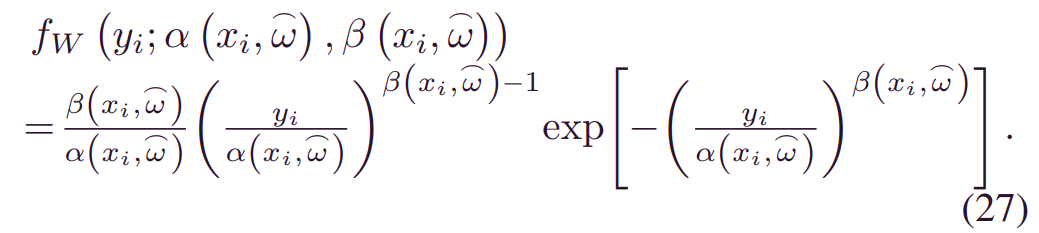
Logistic BDL：Logistic类似于高斯，但尾部较重，理论上增强了鲁棒性。此外，复杂的集成不包括在内：

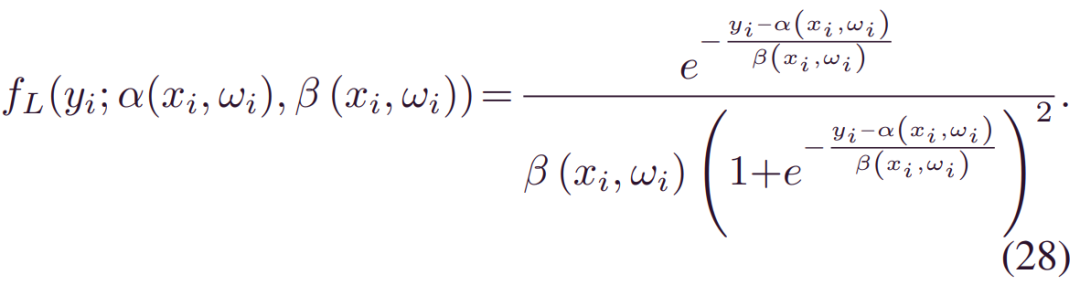
在实践中，离散形式更稳定：

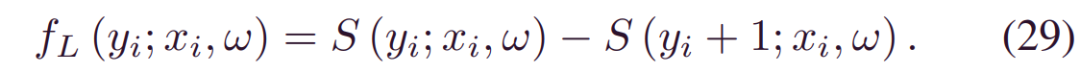
寿命分布可能会影响最终预测分布的形状。由于缺少偏移项，Weibull分布应该覆盖整个轴，表明设备随时可能发生故障。相比之下，Logistic分布对异常值的鲁棒性更高，这使其对异常数据的敏感性降低。因此，如果我们以高斯分布为基准，则Weibull和Logistic假设可以视为保守和激进的选择。对于故障损失较高的设备，优选保守选择。

BDL结构中的激活可分为: 认知层 (α 和 β) 的激活以及一般BNN层的激活。认知层的激活更难选择。它们应该由寿命分布的属性决定。值得注意的是，这三种分布中的参数α控制着产出规模。因此，α-活化应满足以下性质: 1) 保持α非负。2) 能够放大，因为Tanh的输出规模有限。因此，选择指数激活。另一方面，β控制着预测区间的宽度 (高斯和逻辑) 或分布形状 (Weibull)。因此，选择Softplus激活[31]：始终为正，且幅度小于α。

另一方面，一般的激活完全是目标驱动的，应该根据DNN的属性来选择。在我们的案例中，由于GRU[28]，选择了Tanh和Sigmoid激活，这是一种特殊的适合预测预后的问题。但是对于基于图像的任务，由ReLU函数激活的卷积神经网络 (CNN) [32]可能是一个更明智的选择。作为一般框架，此类激活具有高度的灵活性。

4.4

序列贝叶斯RUL 提升算法

通过BDL训练，可以获得基于历史传感器数据_x1:k_为条件的概率RUL预测_φ(yk|x1:k)。因此，沿着数据_x1:1，x1:2，…，x1:k，我们能够依次记录到_φ(y1|x1:1)_，φ(y2|x1:2)，…，φ(yk|x1:k)。值得注意的是，多步RULs之间的内在依赖性可以用来提高预后[33]。为此，我们开发了一种序列贝叶斯提升算法来捕获长期依赖，重点是提高预测精度和压缩CI。该算法包括两个步骤，分别是加权和更新。

步骤1 加权: 我们利用了多个时间步长的RUL预测之间的理论线性关系：

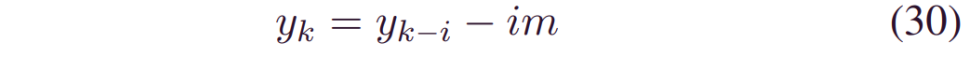
其中m表示时间间隔1 ≤ i ≤ d，d是最大时间步长。可以通过加权平均来建模RUL，_yk_的预测分布，即：

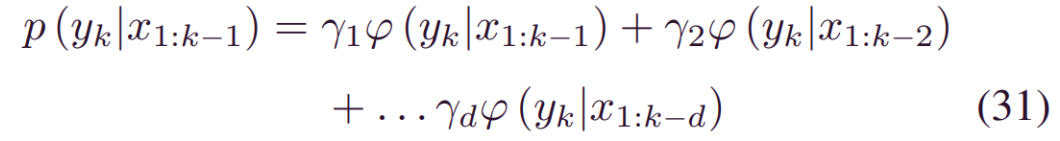
其中_γ1…γd_是每个概率规则的相关权重。基于 (30)，我们有：

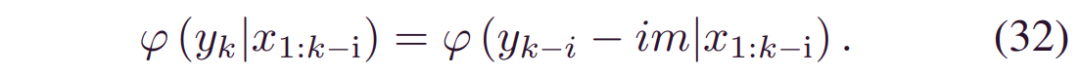
等式 (31) 可以看作是通过移位融合预后结果的加权集合。由于更接近的预测具有更多的可信度，，我们可以将衰减的权重分配给每个RUL：

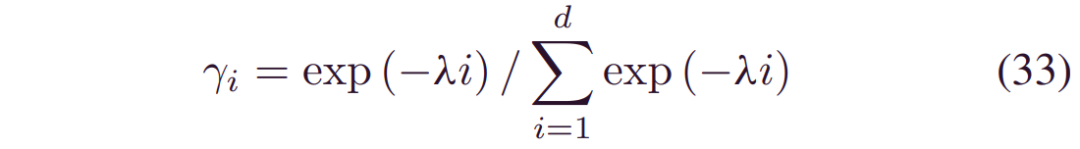
其中λ控制衰减速度。

步骤2 更新：一旦分配了权重，我们就可以通过将_p(yk|x1:k)_与最新的BDL预测_φ(yk|x1:k)结合来更新RUL预测。由于MC采样，(31) 中的预测分布是离散的，它可以表示为与权重相关的一系列离散状态。令{yki,wik|k-1}i=1Ns_代表此类状态和相应的权重。那么，(31) 中的预测分布等价于：

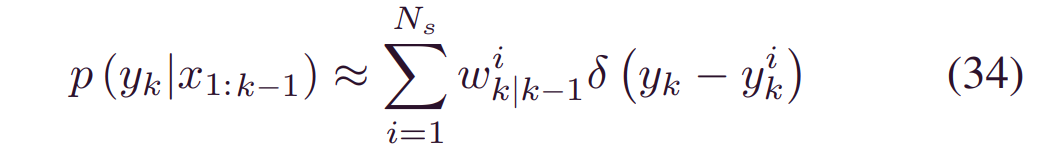
其中，_wik|k-1_与相应的_γ_和_yki_的可能性成正比。在序列贝叶斯方法中，既需要潜在状态，又需要度量值。由于预测融合是在RUL层进行的，我们引入了一个辅助变量_rk_来表示观测函数。它相当于_yk_的最新BDL预测，即：

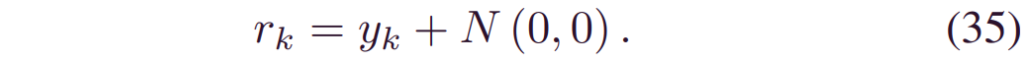
一旦有了新的观测值_xk_，就可以通过贝叶斯更新理论来更新权重，即：

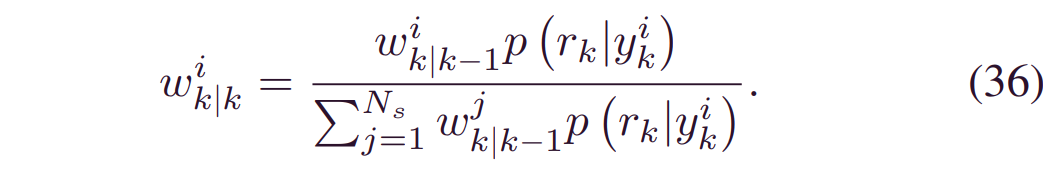
将（35）代入（36）：

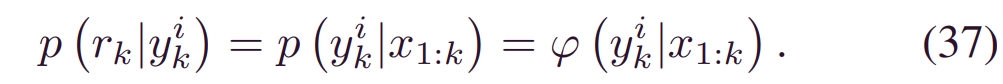
换句话说，可以将最新的BDL预测视为测量函数。因此：

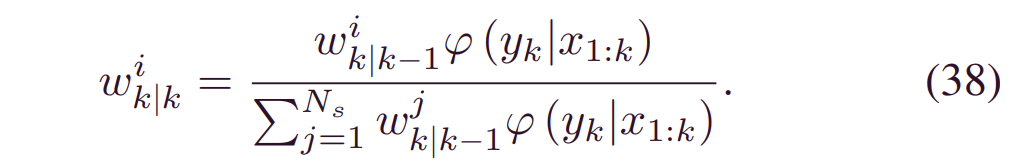
最后，更新后的分布可以写为：

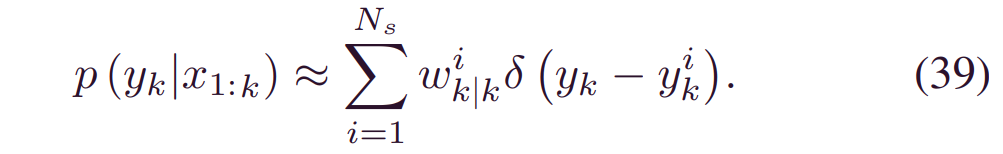
算法2总结了等价过程。

算法2

备注3：Boosting算法与粒子滤波的区别在于预测步骤集成了多个中间结果，并且在更新过程中不需要重要的采样。这种贝叶斯框架可以通过构造长期依赖关系来减轻异常预测的影响，从而增强预测的鲁棒性。同时，更新过程在RUL输出级执行，其中状态和测量函数可以合并到单个BDL模型中。

05

线性异方差实例研究

为了研究数据特征对CI的影响，进行了一个模拟案例研究。假设噪声和有偏数据取自区间[0,12]内的期望y=2x+1和标准偏差(Std)std=0.4x+1的高斯分布。假设数据集的部分丢失，其中间隔[2],[3]和[10],[12]之间的数据被完全删除，而[5]和[8]中的数据被省略了一半。生成这样的特殊数据集来模拟影响不确定性的两个因素，即：异方差噪声和有偏数据集。由于数据集的基本置信区间是已知的，我们可以直接将其与估计的CI进行比较。选择了高斯BDL假设，因为它的任意节点具有明确的物理意义。α节点表征期望的波动，而β节点表示噪声诱导的std。DNN由两个密集层组成，每个密集层有20个节点，通过RELU激活函数连接。

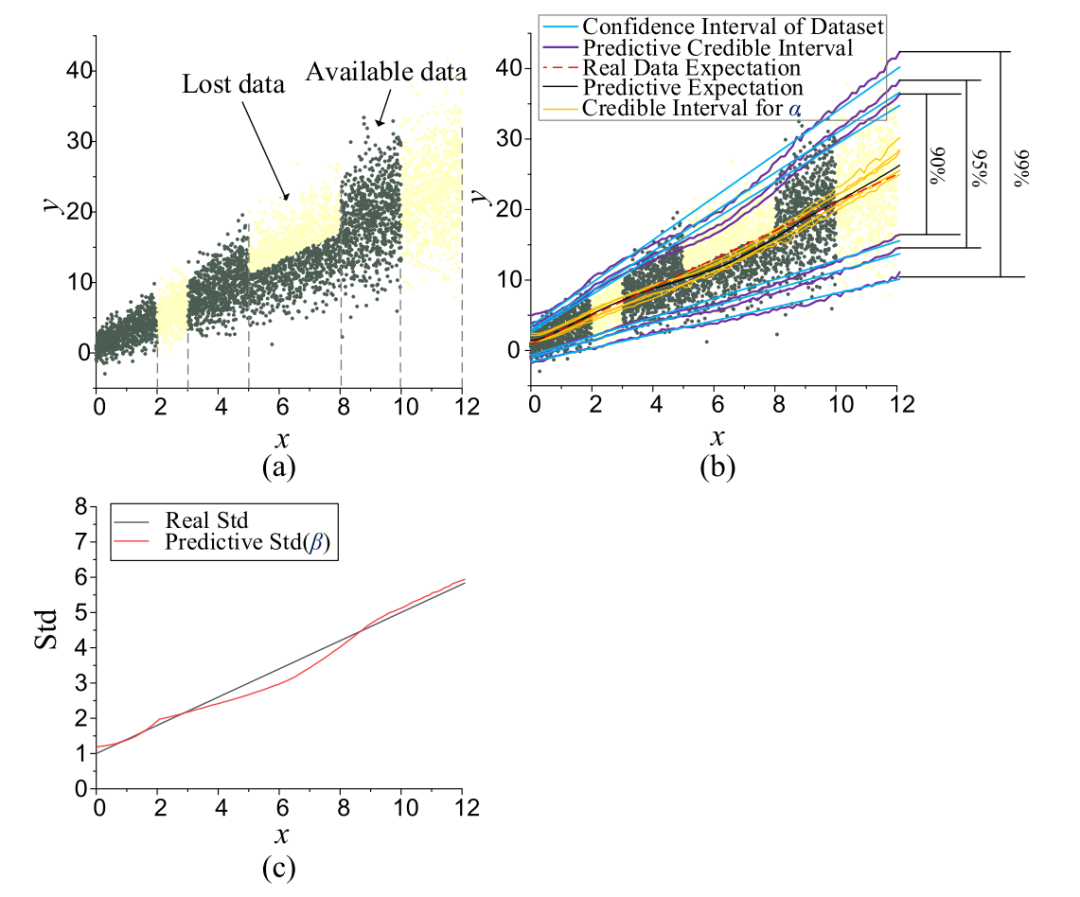
图3：5000个数据的CI (a) 数据集 (b) CI的估计 © β的估计

我们从总共采样5000点开始，如图3(a)所示。值得注意的是，BDL仅使用深色标记的可用数据进行训练，然后重建CI。在图3(b)中分别示出了90%、95%和99%水平的预测CI和真实置信区间。α的CI也是可视化的，以指示认知不确定性的水平。图3©进一步说明了预测Std(β 的期望)与真实Std之间的比较结果，其中陈述了以下三个观察值：

1. 总体而言，估计的CI接近真实置信区间。

2. [2]，[3]和[10]，[12]之间的CI比实际置信区间稍宽，特别是对于[10]，[12]。由于这两个区间内的Std估计在图3©中是准确的，因此CI扩展主要是由于缺失数据或低相邻数据密度引起的认知不确定性。换句话说，在低信息量区域，BDL的认知不确定性往往更大，这与认知不确定性的性质是一致的。

3. 尽管在[5]，[8]之间的y=2x+1上的数据完全丢失，但BDL仍然具有弥补缺失部分的能力。最终估计的CI仅比该区域的真实值略有低估。

为了进行比较，还对只有1000个点的数据集进行了模拟。相应的估计CI如图4所示。观察到的结果具有与图4非常相似的特征。然而，认识的不确定性随着点数的减少而增加，从而导致更宽的CI。这也是合理的，因为在较少可见数据的情况下，贝叶斯模型更难获得高置信度的CIS。

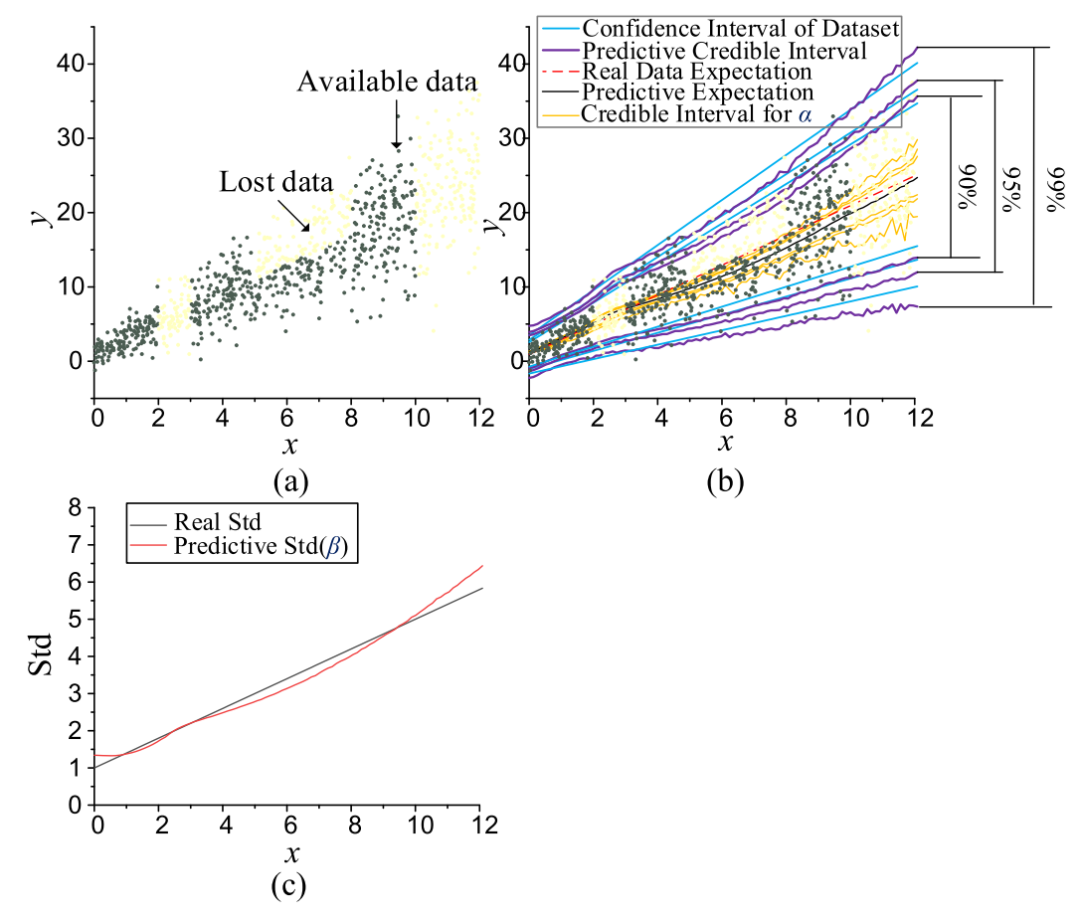
图4：1000个数据的CI (a) 数据集 (b) CI的估计 © β的估计

总之，即使数据丢失或严重偏差，BDL模型也能够估计合理的CIs。训练数据越少，认知不确定性越大。

06

实验数据集

6.1

实验平台

高压断路器是电网中至关重要的设备，其功能是切断短路电流。为了获得真正的故障运行数据，我们对XD组的5个CYA5 220-kV断路器液压机构进行了实验，如图5所示。断路器仅在必要时打开或关闭 (例如，短路故障)，并在其间隔内保持静止。在操作期间，激活信号使线圈通电并产生线圈电流。然后，可移动的铁电枢移动并导致控制阀中的液压油流动。传感器记录线圈电流和气门行程，以监视其健康状况。RUL定义为剩余的运行周期，而每个周期是指一对打开和关闭。每个操作可以在200毫秒内完成，总共产生3000个有效采样点，采样率为15 kHz，可以很好地描述该操作。 每250圈记录一次数据。机构的总运行周期分别为17750、17500、13000、20000、19750。

图5：断路器液压机构实验平台

6.2

特征提取与选择

我们定义了多个特征来捕获机构的健康状态，如图6中典型的闭合波形所示。我们在线圈电流中设置了五个锚_Tc0~Tc4_，并在每个点提取特征。根据行程的速度曲线，整个操作过程分为三个阶段: a) 加速阶段，b) 均匀阶段和c) 减速阶段。这些相的平均速度分别定义为_Vc1,Vc2,Vc3_。

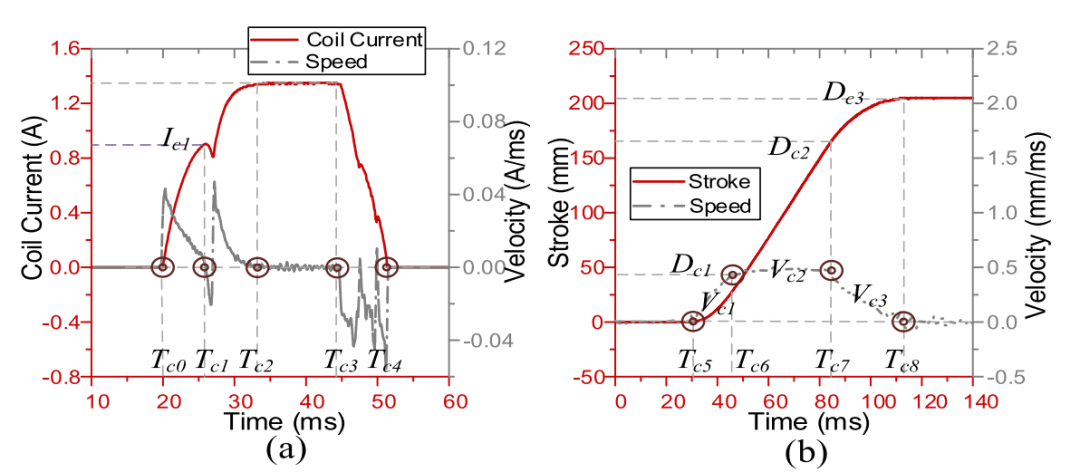
图6：特征提取的关键点。（a）线圈电流。（b）冲程

提取的关闭操作的特征如下:

1. 基本时间点_Tc0~Tc8_。

2. 时间点的值，包括_IC1，_平均值 _(I[Tc2_{Tc3])_，_Var(I[Tc2}Tc3])，_DC1，DC2_和_DC3。

3. 时差，Tc1_Tc0，Tc2Tc0，Tc3_Tc2，Tc4Tc0，Tc8_Tc5，Tc7Tc5，Tc5_Tc5，Tc5Tc0，Tc5_Tc1和Tc8Tc0。

4. 速度，Vc1，Vc2，Vc3，Var(V[Tc6~Tc7])。

5. 等间隔的采样点 (在_Tc2~Tc3_之间)，_ICS1，ICS2，ICS3_和_ICS4_以及点(在_Tc6_和_Tc7_之间的速度曲线上)Vc1，Vc2，Vc3 。

所提取的用于机构开启操作的特征基本相同，共72个特征。选择合适的预后指标可以简化模型学习，尤其是对于工业应用。选择标准包括单调性、可预知性和可趋势性。类似的方法可以在[34]和[35]中找到。主要区别在于，我们利用动态时间规整 (DTW)[36]来表征可趋势性。具体如下：单调性：它测量特征和退化过程之间的一致水平，由：

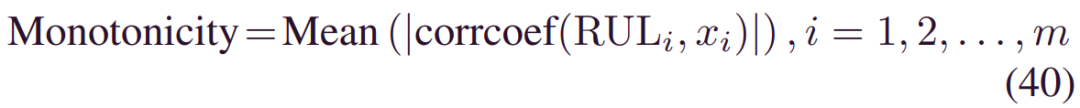
其中m是设备编号，corrcoef(.) 表示皮尔逊系数。由于皮尔逊系数的数学性质，单调性限制为[0,1]。

可趋势性：它指示该特征在整个种群中是否具有相同的基础形状，由：

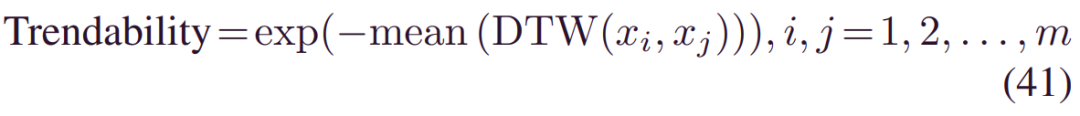
其中DTW(.) 用于测量两个时间序列之间的相似性。然后对平均DTW进行指数加权，以将分数等级限制为[0,1]。

可预测性：它充当单调性和可趋势性之间的平衡标准，即：

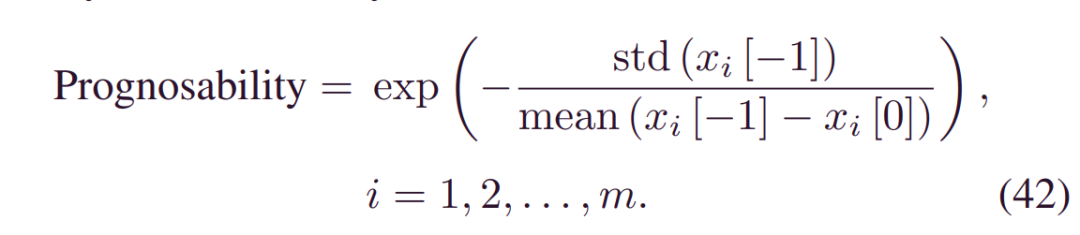
可预测性是每个退化轨迹的最终失效值的偏差除以其均值范围，该均值范围也经过指数加权以获得标准范围[0,1]。该准则不要求特征在整个退化过程中是单调的或相似的，而是强调每个设备的健康或失效值是相似的。

功能的适应度平均为三个指标，因为它们共享相同的数字刻度。在图7中显示了几个具有高适应度的曲线，其中应用了标准化。

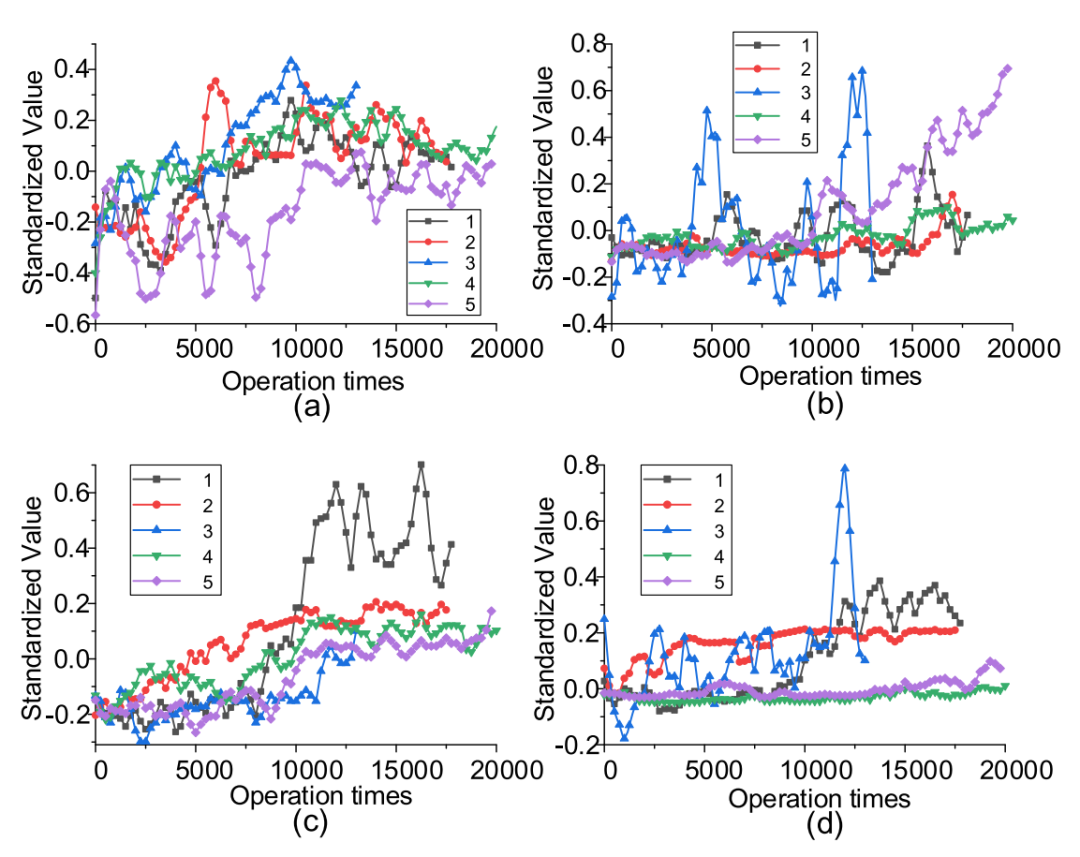
图7：高度拟合的特点

（a）T_{c4}~T_{c0}关闭

（b）Var(V[T_{c6}~T_{c7}])关闭

（c）平均值(I[T_{o2}~T_{o3}])打开时

（d）Var(V[T_{o6}~T_{o7}])打开

6.3

DNN结构

通过上述特征工程，分别从打开和关闭操作中选择了具有较高适应性的前15个特征。使用具有固定起始点的时间窗将时间特征包装成多维输入。由于GRU算法复杂度低，在建立长依赖模型方面性能良好，因此选择GRU作为模型库。 GRU的内部结构如图8所示，由以下方程式控制：

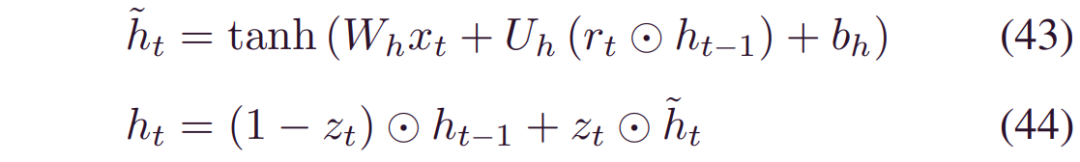
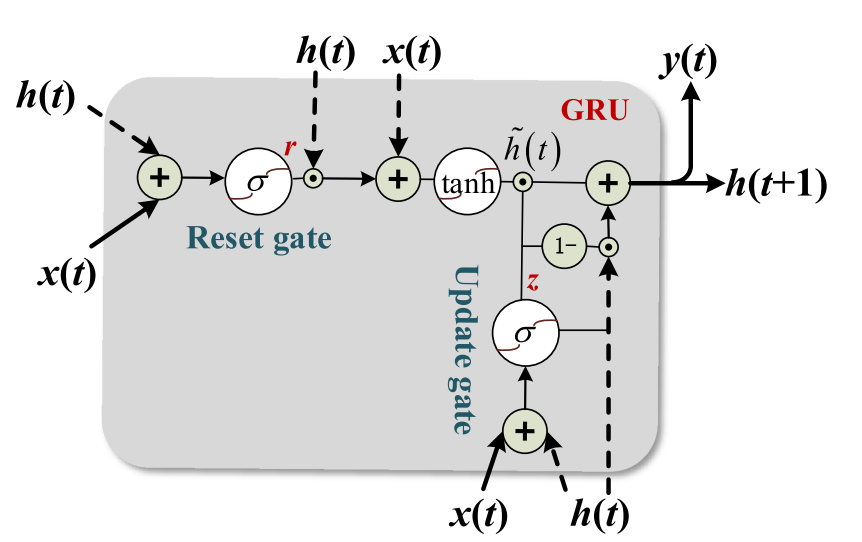
图8：GRU的内部结构

其中，_ht-1_是最后一个时间步的隐藏状态，而_ht_是新更新的状态。_zt_和_ht_是控制信息流的更新和重置门，由：

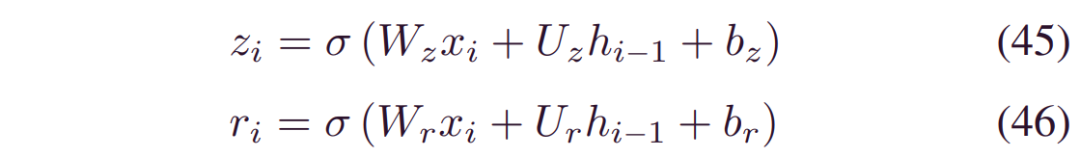
其中_Wz，Uz，Wr，Ur_是权重，_br，bz_是偏差。Σ 是sigmoid函数。在此公式中，重置门删除与最终任务无关的信息，而更新门控制先前隐藏状态和新观察之间的积分百分比。通过一步融合忘记门和选择性内存，GRU与LSTM相比节省了一个门，因此参数更少。

通过多层RNN的叠加，可以获得更深的学习结构和更强的学习能力。在堆叠GRU中，前一层中每个时间步的隐藏状态被视为下一层的输入。最后，最终层的最新输出与认知层连接。堆叠的BDL结构如图9所示，其中每个圆形代表完整的GRU单元。由于我们的训练集是中等规模的，因此选择了具有两个递归层的GRU，其中每个隐藏状态包含十个递归维度。

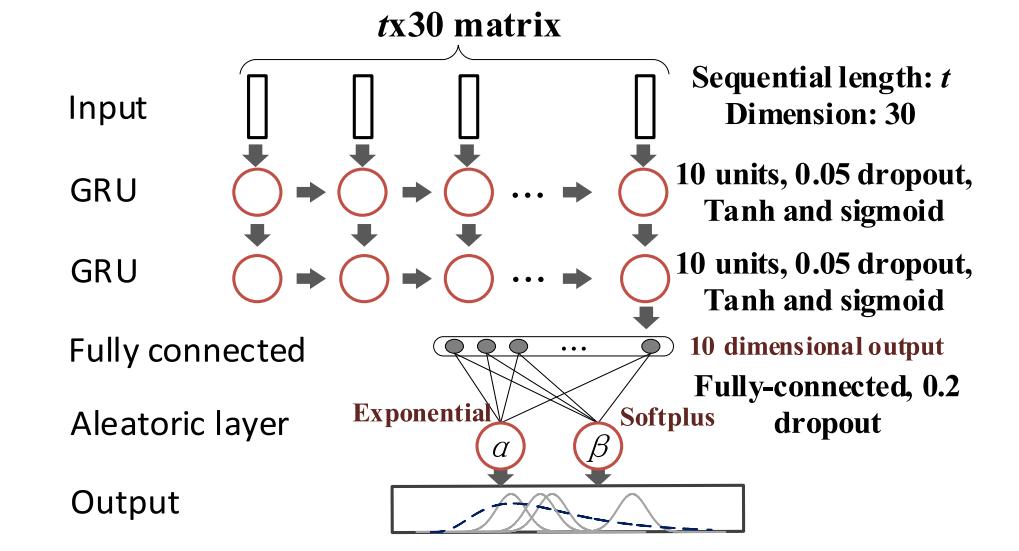
图9：BDL的结构

值得注意的是，认知层包含两个定义寿命分布的节点。GRU的输出通过指数和softplus激活完全连接到认知层，即：

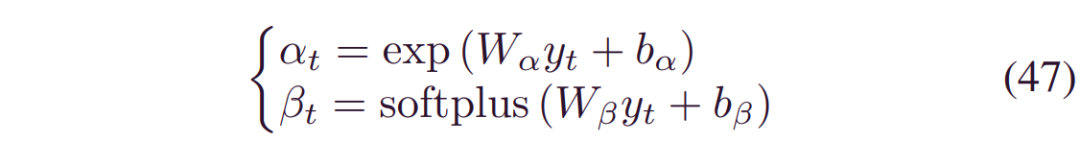
其中，Wα，_Wβ_表示权重，bα，_bβ_是偏差。在GRU层中，为了提高稳定性，dropout被设置为0.05，在完全连接层中，dropout被设置为0.2。因此，GRU的作用更像是高级特征提取器，而密集连接在对认知不确定性进行建模时更加活跃。模型应用在windows 64位上，带有GTX1050Ti GPU和16gb RAM。学习速率为0.001的RMSprop用于训练模型。

6.4

评价指标

采用不同的性能指标，从均值的点估计和不确定度两个方面对模型的性能进行评价。 前者包括均方根误差(RMSE)、平均绝对误差(MAE)和对称平均绝对百分比误差(SMAPE)。 第二类包括预测间隔的覆盖概率(PICP)和平均预测间隔宽度(MPIW)。指定后，由N个样本的相对误差给出SMAPE：

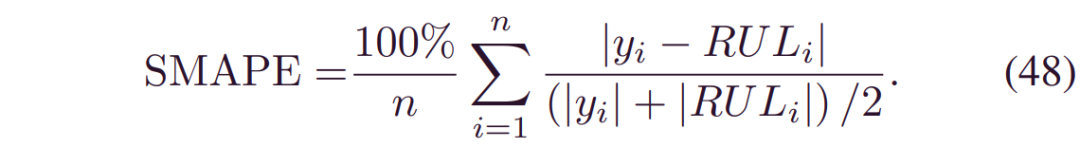
PICP决定实际RUL是否在CI内，即：

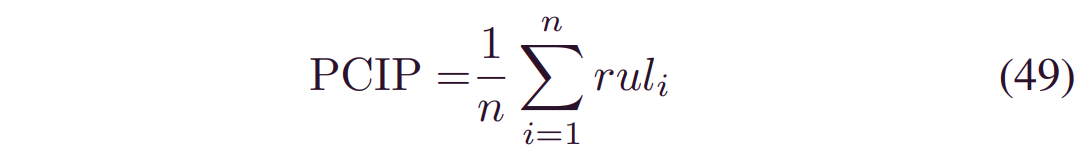
其中，ruli=1如果_Li_≤_RULi_≤_H_，否则为0；_Hi_和_Li_是CIS的上下界。 MPIW是CI的平均宽度。PICP和MPIW是相互冲突的度量标准，因为较窄的MPIW肯定会降低PICP。

07

实验结果

本部分首先分析了MC算法的收敛性，然后将BDL算法与几种概率基线算法的性能进行了比较。

7.1

MC采样的收敛性（算法2）

在算法1中，蒙特卡罗(MC)抽样表明，随着M和B的增大，逼近效果越来越好。 然而，一个合适的MC采样大小必须在计算复杂度和精度之间取得平衡。 图 10给出了M和B上一个特殊的RUL分布的收敛面，用期望值和方差来度量。 这种情况是在时间步1250的Weibull BDL上，具有更大的预测方差，因此具有更大的收敛困难。 在B超过50后，估计保持相当稳定。因此，为了更好的准确性，在实验中将这两个系数设置为100。M=100的平均采样时间为0.016s，B=100的平均采样时间为9.66e-6s，这是可以接受的。M迭代占用了大部分时间。

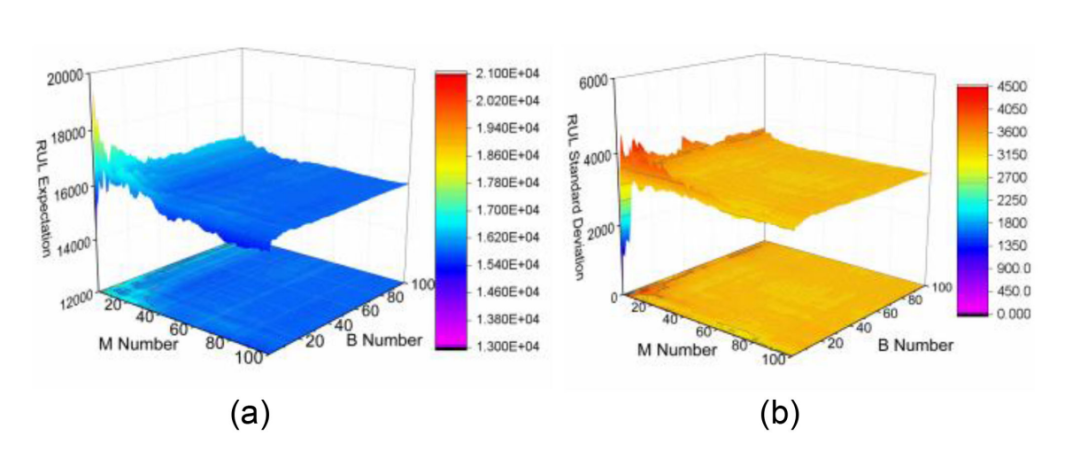
图10：MC收敛于M和B（a）期望（b）标准

7.2

不同BDL损失函数的比较

在这一部分中，我们在IV-C部分测试了三个BDL的性能。 使用交叉验证中的保留一出的思想，将五个运行到失败的机器中的每一个分离并测试，总共生成五个训练/测试集。 表一显示了RUL在五个试验中的平均CI为90%，图11给出了在机器5的90%、95%、99%顺式下预测规则与真实规则之间的比较，其中偶然、认知的和总的不确定性也被可视化。值得注意的是，(3)中总不确定度的和律是用方差来度量的。 然而，方差在RUL的平方维。 为了使不确定度与RUL具有可比性，我们用方差的平方根，即不确定度的标准差代替图 11。

表1：三种BDL的性能

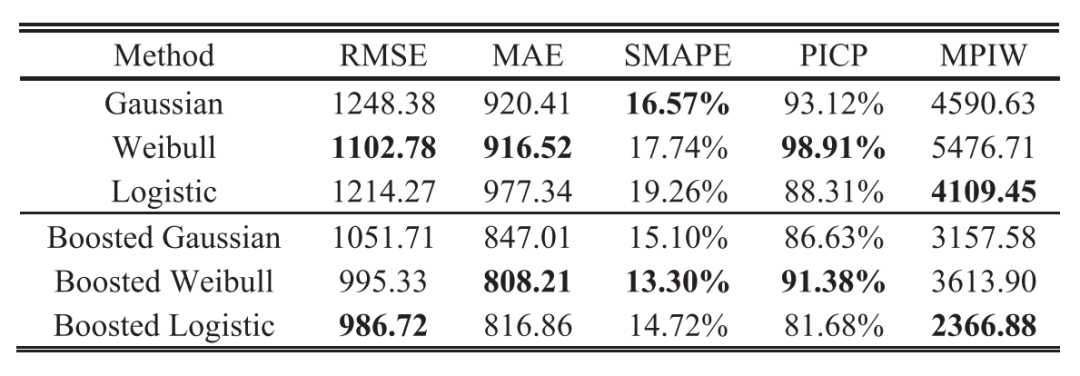
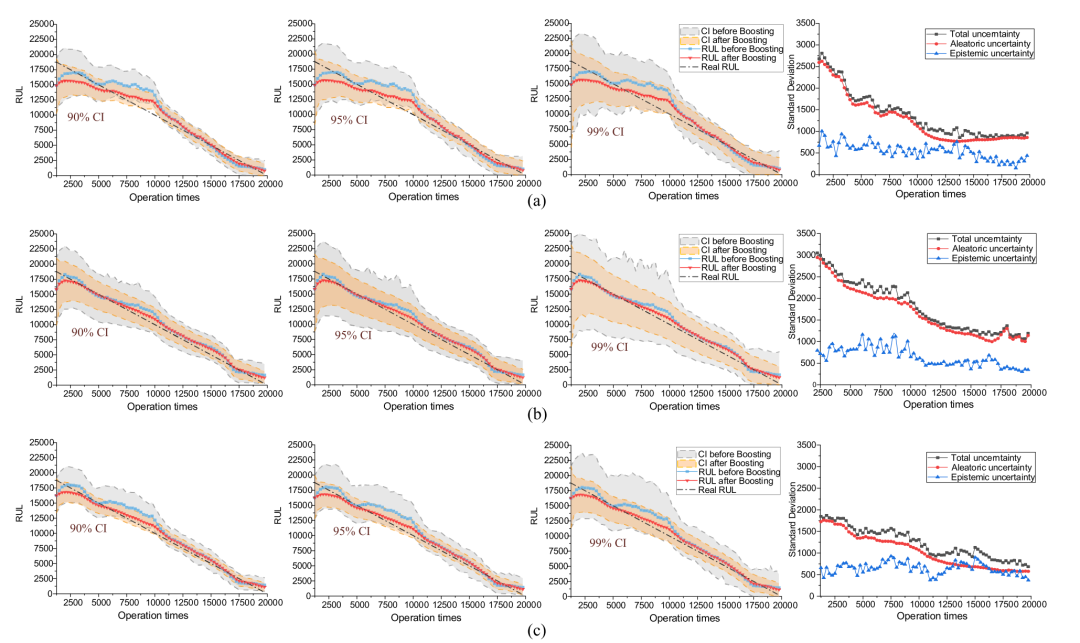
图11：使用CI和不确定性量化进行RUL预测（a）Gaussian BDL（b）Weibull BDL（c）Logistic BDL

显然，三种BDL模型都能捕捉到液压机构的退化趋势，而Weibull BDL模型提供了最高的点估计精度。 此外，Logistic BDL的得分最高，为19.26%，而Gaussian和Weibull在这一指标上的表现相似。 Weibull分布也提供了更高的PICP98.91%。但是，它也会导致MPIW所指示的最宽的CI。为此，我们进一步测试了PICP和MPIW的无线电，这反映了CI的效率。图12说明了三个BDL的CI效率。Weibull BDL的PICP值最高，但效率最低，而Gaussian BDL和Logistic BDL的PICP值非常相似。由于缺少偏移项，Weibull分布导致CI较宽，效率较低。此外，Logistic分布在形状上类似于高斯分布，但尾部较重。因此，这两个分布具有相似的效率，但前者的绝对值更窄。

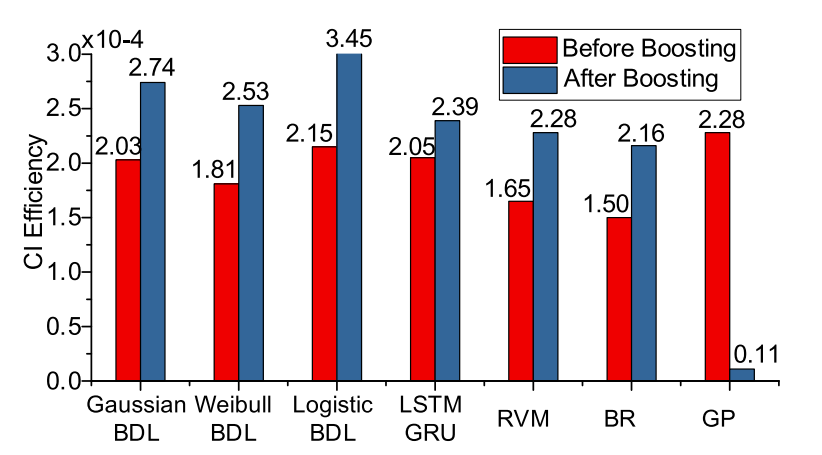
图12 拟定BDL和基线的CI效率

图 11还表明，偶然不确定性占主导地位，且随着数据的增加呈递减趋势，而认知不确定性相对稳定。这种现象归因于不确定因素的累积效应。 如前所述，认知只与训练集的大小有关。在一个充分训练的模型下，它在每次预后中都保持稳定。 然而，任意的不确定性是由噪声引起的。在相同的噪声程度下，较长的预测时间会积累较重的噪声诱导不确定性。这就解释了为什么在开始时，偶然的不确定性似乎很重要，因为未知的轨迹更长。

当应用所提出的贝叶斯提升算法时，预测结果总是优于以前的预测结果，如表1和图11所示以Weibull BDL为例，在图13上对提升算法前后的分布进行了可视化。结果显示了更少的波动、更好的单调性和更高程度的中心密度。此外，图12表明提升算法也提高了CI效率。

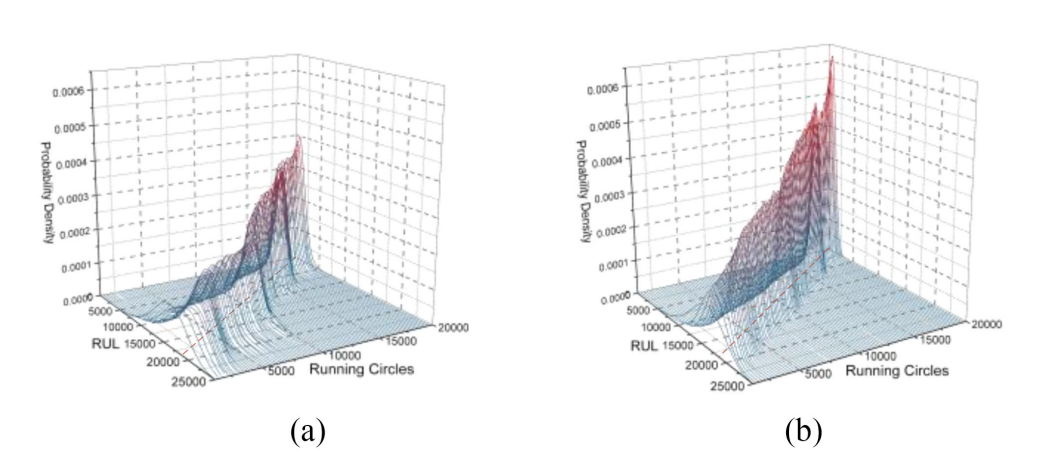
图13：RUL的预测分布（a）贝叶斯提升之前（b）贝叶斯提升后

7.3

与其它概率模型的比较

为了验证BDL模型的优越性，还实现了四种不同的预测方法。 包括一个具有RMSE损耗的标准GRU（RMSE-GRU）和相同的DL结构。选择20%的波动作为其CI。此外，同样的数据也应用于几种流行的概率模型，包括相关支持机(RVM)、贝叶斯岭回归(BRR)和高斯过程(GP)。表II总结了模型的性能。图 14还显示了具有90%CI的预测规则和机器5的真实规则，其中只有总的不确定性可以被可视化。

从表II中可以清楚地看出，高斯/Weibull/Logistic BDLS比RMSE-GRU能获得更好的点估计。理论上，高斯BDL可以看作是RMSE-GRU的贝叶斯版本。 因此，证明了贝叶斯先验能提高DL的泛化能力。RMSE-GRU在点估计方面优于RVM、BR和GP。 但其实际PICPS仅为73.90%。比较而言，RVM和BR的PICPS更容易被接受。然而，与基于BDL的方法相比，它们的点估计值相对较低。GP的CI最差，PICP最低，为39.42%，说明GP的成功很大程度上依赖于复杂的核函数设计。 最后，RVM、BR、GP的不确定性不能随着信息量的增加而减少，如图所示14。

表2：其他概率方法的性能

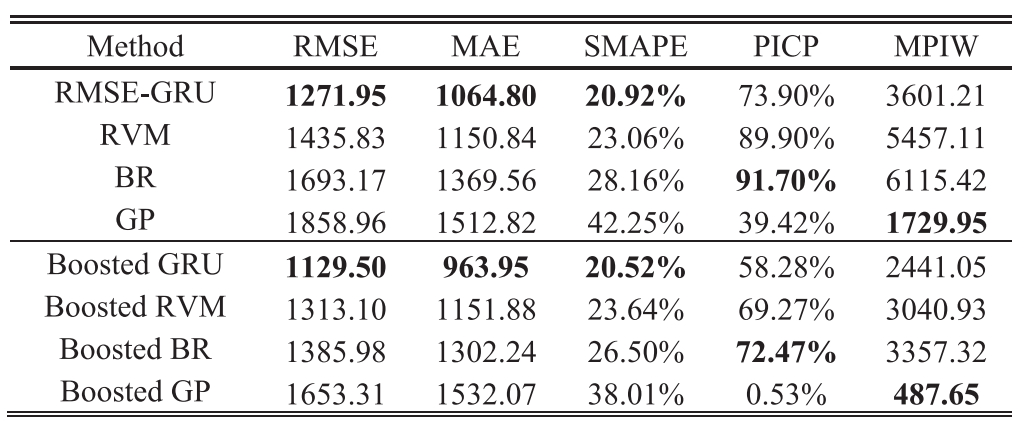
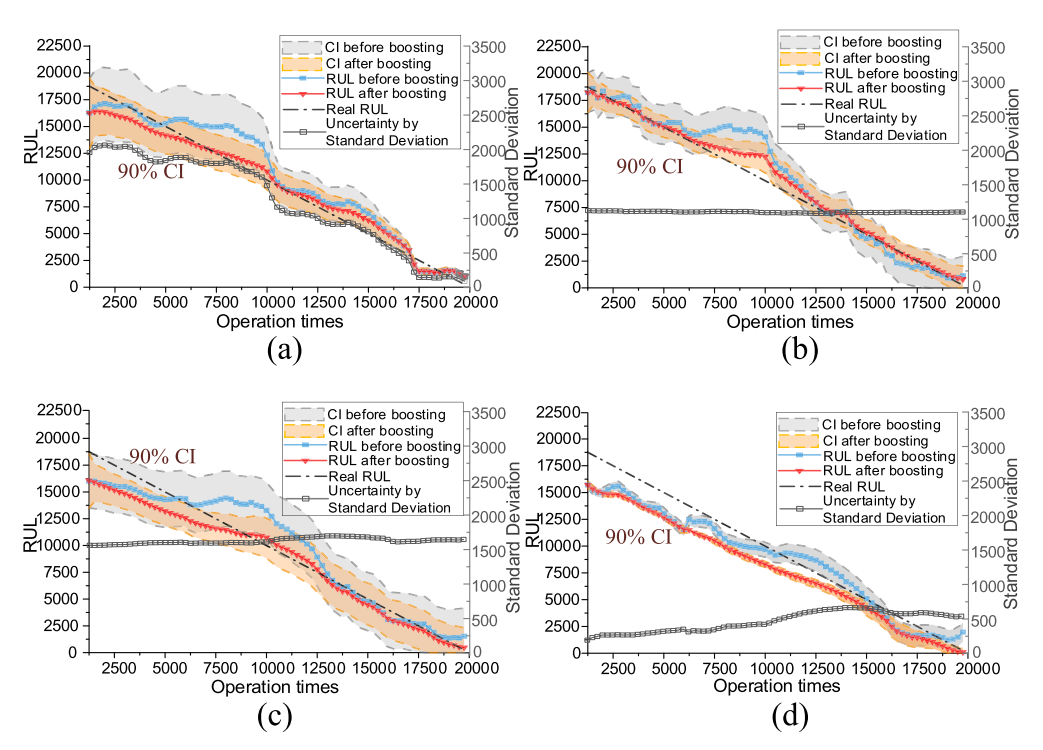
图14：90%置信区间的RUL

（a）RMSE-GRU（b） RVM（c）BR（D）GP

应用提升算法后，GRU、RVM和BR的性能也得到了改善，具有较低的RMSES、MAES和SMPAPS。 另一方面，CIS收缩并导致更差的PICPS，这与表I类似。在GP中观察到一个例外，这是由于每条轨迹开始时都有相似的趋势。然后，提升算法失去跟踪。这一观察表明，可靠的CIS对序列提升算法成功的重要性。

总之，BDL提供了更高的估计精度，并在CI宽度和覆盖面积之间取得了令人满意的平衡。算法可以有效地缩小预测CI，提高预测CI的效率。

08

总结

本文提出了一种基于BDL的RUL预测框架，该框架能够捕捉到异方差偶然不确定性和认知不确定性对RUL预测的综合影响。将先验分布分配给GRU神经网络的每个权重，以捕获认知不确定性。 另一方面，通过将神经网络的输出分解为寿命分布的先验信息来量化与输入相关的认知不确定性。提出了一种新的序列贝叶斯提升算法，通过将状态转移和观测统一到一个单一的BDL模型来进一步改进RUL估计。

通过实际断路器液压机构数据集验证了该框架的性能。 实验结果表明，在提高估计精度和CI宽度与PICP的平衡方面，本文提出的方法优于传统的RMSE损失的GRU模型和几种传统的概率模型。我们的序列贝叶斯提升算法进一步增强了这种优越性。目前工作的一个可行的扩展是将BDL框架与基于模型的预测方法结合起来。

微信号reliability_ustb

USTB可靠性小站

点击“阅读原文”获取英文版原文，提取码：969h