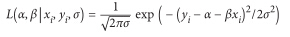白手起家学习数据科学 ——线性回归之“简单线性回归篇”(十一)

本文主要是介绍白手起家学习数据科学 ——线性回归之“简单线性回归篇”(十一)，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

在前面的章节中，我们使用相关系数函数测量2个变量之间线性相关的强度，对于大多数应用只是知道线性相关是不够的，我们想要理解这个关系的本质，我们会使用简单线性回归来加以理解。

The Model

有2个变量，一个是DataSciencester网站用户的数量，另一个是每个用户在这个网站上每天所花费的时间。假设你自己确信有更多朋友引起人们在这个网站上花费更多的时间。

Engagement部门的副总要求你建立一个模型，描述这个关系。由于你发现一个极其强的线性关系，自然的你会开启一个线性模型。

尤其，你假设有2个常量$\alpha$(alpha)和$\beta$(beta)：
$yi = {\alpha}xi + {\beta} + {\sigma}i$

$yi$是用户$i$在网站上每天花费多少分钟，$xi$是用户$i$有多少朋友，${\sigma}i$是一个误差项，表示有其他因素没有计算到这个简单模型中。

假设我们确定alpha和beta，那么我们能简单的做出预测：

def predict(alpha, beta, x_i):return beta * x_i + alpha

那么，我们怎样选择alpha和beta？首先我们选择任意的alpha和beta，对于输入x_i会有一个预测的输出，由于我们知道真实的输出y_i，我们能计算每对的误差：

def error(alpha, beta, x_i, y_i):"""the error from predicting beta * x_i + alphawhen the actual value is y_i"""return y_i - predict(alpha, beta, x_i)

我们想要知道的是全部数据集的总体误差，但是我们不想只是简单的把误差相加—-如果x_1预测是正值，x_2预测是负值，那么这2个误差可能互相抵消。

所以，代替的解决方案是求误差的平方和：

def sum_of_squared_errors(alpha, beta, x, y):return sum(error(alpha, beta, x_i, y_i) ** 2for x_i, y_i in zip(x, y))

最小二乘法(least squares solution)是选出的alpha和beta，让sum_of_squared_errors尽可能的小。

使用微积分(或者乏味的代数)，最小化误差得到的alpha和beta是：

def least_squares_fit(x, y):"""given training values for x and y,find the least-squares values of alpha and beta"""beta = correlation(x, y) * standard_deviation(y) / standard_deviation(x)alpha = mean(y) - beta * mean(x)return alpha, beta

我们没有仔细检查数学公式，让我们考虑为什么这个是一个合理的解决方案，alpha的选择简单的说是当我们计算出独立变量x的平均值时，我们预测因变量y的平均值。

beta的选择意思是，当输入值增加了standard_deviation(x)，预测增加了correlation(x,y)*standard_deviation(y)。在这个案例中，当x与y是完美的正相关，那么x增加一个standard deviation引起预测的y增加一个standard-deviation；当他们是完美的负相关时，x增加引起预测y的减小；当相关系数是0时，意思是x的改变不能影响预测的y值。

很容易应用这个到减少离群值：

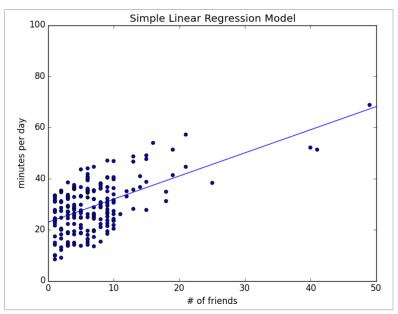
alpha, beta = least_squares_fit(num_friends_good, daily_minutes_good)

计算结果alpha = 22.95，beta = 0.903，所以我们的模型预测有n个朋友的用户每天花费$22.95 + n * 0.903$分钟在这个网站上。我们预测没有朋友的用户每天花费23分钟在这个网站上，每增加一个朋友，预测这个用户会多花一分钟的时间在这个网站。

在下图中，我们画出预测线，了解模型怎样拟合观察数据。

当然，我们需要更好的方法理解我们拟合数据的程度，而不是盯着图看，一个普遍的测量是决定系数(或者叫R方)，测量的是变量发生变化的部分：

def total_sum_of_squares(y):"""the total squared variation of y_i's from their mean"""return sum(v ** 2 for v in de_mean(y))def r_squared(alpha, beta, x, y):"""the fraction of variation in y captured by the model, which equals1 - the fraction of variation in y not captured by the model"""return 1.0 - (sum_of_squared_errors(alpha, beta, x, y) /total_sum_of_squares(y))r_squared(alpha, beta, num_friends_good, daily_minutes_good) # 0.329

现在，我们选择alpha和beta，以使误差的平方和最小化。我们选择的线性模型是”总是预测mean(y)”(对应alpha = mean(y)和beta = 0)，它的 sum of squared errors等于它的total sum of squares。意思是R方等于0，暗示一个模型几乎总是等于均值。

很显然，最小二乘模型最差劲的情况下，也就是和上面的模型一样，意思是sum of the squared errors最大是total sum of squares，R方最小是0； sum of squared errors最小是0，R方最大是1。

R方越大，模型拟合的越好。这里我们计算R方等于0.329，告诉我们，我们的模型只是稍微拟合这个数据，很显然还有其他因素的影响。

使用梯度下降法

如果我们要求$theta = [alpha, beta]$，那么我们也能使用梯度下降法(gradient descent)解决这个问题：

def squared_error(x_i, y_i, theta):alpha, beta = thetareturn error(alpha, beta, x_i, y_i) ** 2def squared_error_gradient(x_i, y_i, theta):alpha, beta = thetareturn [-2 * error(alpha, beta, x_i, y_i), # alpha partial derivative-2 * error(alpha, beta, x_i, y_i) * x_i] # beta partial derivative# choose random value to start
random.seed(0)
theta = [random.random(), random.random()]
alpha, beta = minimize_stochastic(squared_error,squared_error_gradient,num_friends_good,daily_minutes_good,theta,0.0001)
print alpha, beta

使用相同的数据，我们能得到alpha = 22.93，beta = 0.905，这个数字非常接近真实的答案。

最大似然估计

为什么要选择最小二乘法，一个判断理由涉及最大似然估计(maximum likelihood estimation)。设想我们有一组样本$v1,...,vn$来自一个分布，这个分布依赖一些位置参数$\theta$。
$p(v1,...,vn|{\theta})$

如果我们不知道theta，我们能调换位置，把这个数看成已知样本下$\theta$的概率：
$L({\theta|v1,...,vn})$

在这种方法下，最可能的$\theta$值是最大化概率函数的情况，即，让观察到的数据最大化概率的值。在连续型分布的案例中，我们有一个概率分布函数而不是概率密度函数，在这种情况下，我们能做相同的事情(因为一般情况下连续型给出的都是概率密度函数)。

回到线性回归中，设想线性回归中的误差服从均值为0，方差为$\sigma$的整体分布，如果是这种情况，那么基于(x_i, y_i)的概率是：

基于全部数据集的似然函数是单个似然的乘积，当选择的alpha和beta最小化误差平方和时精确度最大。即，在本例中，最小化误差平方和等价于最大化观察数据的概率。

下一章节中我们将要介绍多元回归。

这篇关于白手起家学习数据科学 ——线性回归之“简单线性回归篇”(十一)的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---