蓝桥杯--数论2 AcWing 1296. 聪明的燕姿（因数和定理）

城市中人们总是拿着号码牌，不停寻找，不断匹配，可是谁也不知道自己等的那个人是谁。
可是燕姿不一样，燕姿知道自己等的人是谁，因为燕姿数学学得好！
燕姿发现了一个神奇的算法：假设自己的号码牌上写着数字 S，那么自己等的人手上的号码牌数字的所有正约数之和必定等于 S。
所以燕姿总是拿着号码牌在地铁和人海找数字（喂！这样真的靠谱吗）。
可是她忙着唱《绿光》，想拜托你写一个程序能够快速地找到所有自己等的人。
输入格式
输入包含 k 组数据。
对于每组数据，输入包含一个号码牌 S。
输出格式
对于每组数据，输出有两行。
第一行包含一个整数 m，表示有 m 个等的人。
第二行包含相应的 m 个数，表示所有等的人的号码牌。
注意：你输出的号码牌必须按照升序排列。
数据范围
1≤k≤100,
1≤S≤2×109
输入样例：
42
输出样例：
3
20 26 41

题意：给出一个数S，求出所有因数和等于S的数

数论基本就一题一个定理，没学过定理就得从头先学定理再编成代码痛苦的一批

这题主要涉及到约数个数和约数之和两个定理，从分解式来看

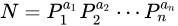
对于约数个数来说，每个约数都由质因子的不同次幂组成，且每个质因子指数都可以从1~ai，计算组合种类，那么N的约数个数则为

(1+a1)(1+a2)…(1+a3)

对于约数之和来说，先给出公式如下

(1+p1+p1²+…+p1^a1)(1+p2+p2²+…+p2^a2)…(1+pn+pn²+…+pn^an)

其实也很好理解，每次从一个括号中取出一个质数的n次幂，会组合成一个新的因数，将各种组合列出相加再化简即可，此题核心也就是这个定理

首先要预估一下，其实满足约数和等于S的数是很少的，如果暴力枚举从1~S-1会很浪费时间，因此可以通过枚举每个括号的pi和ai，如果S能够整除这一项，那么递归去计算n除上这项的值，递归至S更新为1结束

for(p : 2,3,5,7,...)for(a : 1,2,3,...)if(S mod (1+p1+p1^2+...+p1^a1) == 0)dfs(下一层)

主要在于如果这种方式搜索的话还是会爆，需要考虑尽可能的剪枝
1.pi的枚举至sqrt（S）即可，同时枚举的pi要大于p(i-1)
2.如果S-1为质数，可直接作为一种答案

另一方面，定义的dfs函数要有三个传参
last：记录上一质因数的下标，以便找到大于它的下一质因数
product：记录每项质因数的最高次幂值，累乘至最后即为所求
S：当前剩余约数和

这里还是有很多细节没有写出来，只是简记了一下思路，具体可以参考https://www.acwing.com/solution/content/10545/，究极详细

放上代码

import java.io.*;
import java.util.*;public class Main {static Scanner tab = new Scanner(System.in);static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));static BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));static int N = 50010;static int primes []=new int [N];static boolean st[]=new boolean [N];static int cnt;static int ans[]=new int [N];static int len=0;//判断素数static boolean is_prime(int x) {if(x<N)return !st[x];for(int i=0;primes[i]<=x/primes[i];i++)if(x%primes[i]==0)return false;return true;}//搜索查找static void dfs(int last, int prod, int s) {//s==1时说明递归结束，直接记录答案返回if(s==1) {ans[len++]=prod;return ;}//当S-1即一项中p^1^是素数且大于上一质因数时，可以直接记录为一种答案if( s-1 > (last<0?1:primes[last])&&is_prime(s-1))ans[len++]=prod*(s-1);//枚举pifor(int i=last+1;primes[i]<=s/primes[i];i++) {int p=primes[i];//枚举ai并记录最高次项for(int j=1+p,t=p;j<=s;t*=p,j+=t) {if(s%j==0)dfs(i,prod*t,s/j);}}}//素数打表static void get_primes(int n) {for(int i=2;i<n;i++) {if(!st[i]) {primes[cnt++]=i;}for(int j=0;primes[j]*i<=n;j++) {int t=primes[j]*i;st[t]=true;if(i%primes[j]==0) {break;}}	}}public static void main(String[] args) throws IOException {get_primes(N-1);while(tab.hasNext()) {len=0;int s=tab.nextInt();//初始化下标为-1便于后面判断dfs(-1, 1, s);System.out.println(len);if(len>0) {Arrays.sort(ans,0,len);for(int i =0;i<len;i++) {System.out.print(ans[i]+" ");}System.out.println();}}}
}

一题一天系列