磁盘调度最短寻道时间优先算法(SSTF)C++实现

本文主要是介绍磁盘调度最短寻道时间优先算法(SSTF)C++实现，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

最近在腾讯的笔试题中看到最短寻道时间的题目，然后就去看了下相关资料，了解了下SSTF算法的实现（原理就是优先访问离当前读写头最近的位置）

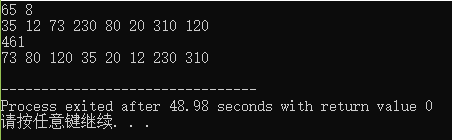
例如：磁盘访问序列为：35，12，73，230，80，20，310，120

读写头起始位置为：65磁道处

那么SSTF走道顺序依次为：65，73，80，120，35，20，12，230，310

磁头走过总道数为：461

C++代码实现如下

#include<iostream>
#include<math.h>
using namespace std;
int sstf(int *a,int *b,int start,int N)
{int sum,min,index,k,s_index,c[1000]={0};//c[]访问过的数字标记为1；s_index=sum=k=0;for(int j=0;j<N;j++){s_index=index=0;//把初始第0位数标记为初始的距离最小值，并记录index，如果第0位已经访问过，则往后移一位 while(true){if(c[s_index]==0){min=abs(start-a[s_index]);index=s_index; break;}else{s_index++;}}		for(int i=s_index;i<N;i++){if((abs(start-a[i])<min)&&c[i]==0)//判断是否比前一个比较过的数要小并且是否已经访问过 {min=abs(start-a[i]);index=i;//index每次找到的距离最小的数的index记录下来 }}c[index]=1;//把访问过的数用数组c记录下来 sum+=min;//当前数和访问到的数之间的最短距离记录累加 b[k++]=a[index];//把访问过的数存到数组b中 start=a[index];//更新当前所在的数 }return sum;
}
int main()
{int a[1000]={0},b[1000]={0};int start,num;//start为初始值，num为要输入的数的个数 cin>>start>>num;for(int i=0;i<num;i++)cin>>a[i];cout<<sstf(a,b,start,num)<<endl;for(int i=0;i<num;i++)cout<<b[i]<<" ";cout<<endl; return 0; 
}