线性代数（六）| 二次型 标准型转换 正定二次型 正定矩阵

2023-11-10 08:01
文章标签 转换 矩阵 线性代数 二次 标准型 正定

本文主要是介绍线性代数（六）| 二次型 标准型转换 正定二次型 正定矩阵，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

文章目录

  • 1. 二次型化为标准型
    • 1.1 正交变换法
    • 1.2 配方法
  • 2 . 正定二次型与正定矩阵

1. 二次型化为标准型

和第五章有什么样的联系

首先上一章我们说过对于对称矩阵，一定存在一个正交矩阵Q，使得$Q^{-1}AQ=B $ B为对角矩阵

那么这一章中，我们讲到，二次型写成矩阵后本质上就是一个对称矩阵，而我们想把它变的标准型，不就正好是一个对角矩阵，那么实际上我们的这个化标准型，本质上不就是矩阵对角化吗

但我们在上一章中是$Q^{-1}AQ=B $ 引入的 矩阵关系叫矩阵相似

而在这一章中是$Q^{T}AQ=B $ 引入的矩阵关系叫矩阵合同

有同学会很好奇，那这不是不一样嘛，而我们其实了解到，对于正交矩阵 Q − 1 = Q T Q^{-1}=Q^T Q−1=QT ，也就不难理解他们是一样的了

1.1 正交变换法

（1）求矩阵特征值和特征向量

（2）特征向量正交化和单位化
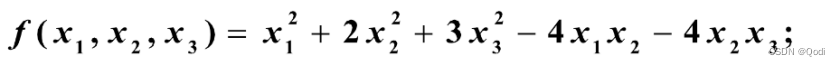
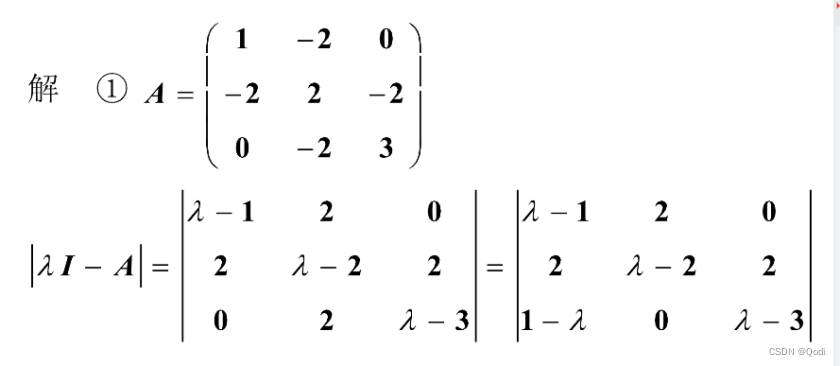
在这里插入图片描述

在这里插入图片描述

在这里插入图片描述

外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传

1.2 配方法

一般用到比较少

2 . 正定二次型与正定矩阵

​ 等价关系

（1）二次型 X T A X X^TAX XTAX是>0的

（2）A是正定矩阵

（3）A的正惯性指数是n

（4）A合同于单位矩阵

（5）A的特征值都是正数

（6）A的顺序主子式都大于零

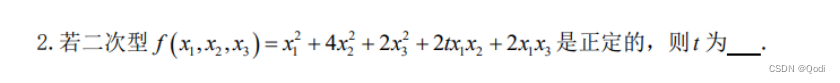
在这里插入图片描述

​ 可以写出二次型矩阵 ( 1 t 1 t 4 0 1 0 2 ) \begin{pmatrix}1&t&1\\t&4&0\\1&0&2\end{pmatrix} ​1t1​t40​102​ ​ 另它的行列式大于零即可

这篇关于线性代数（六）| 二次型 标准型转换 正定二次型 正定矩阵的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/381396。

相关文章

hdu 4565 推倒公式+矩阵快速幂

hdu 4565 推倒公式+矩阵快速幂

题意 求下式的值： Sn=⌈ (a+b√)n⌉%m S_n = \lceil\ (a + \sqrt{b}) ^ n \rceil\% m 其中： 0<a,m<215 0< a, m < 2^{15} 0<b,n<231 0 < b, n < 2^{31} (a−1)2<b<a2 (a-1)^2< b < a^2 解析 令： An=(a+b√)n A_n = (a +
阅读更多...
线性代数|机器学习-P36在图中找聚类

线性代数|机器学习-P36在图中找聚类

文章目录 1. 常见图结构2. 谱聚类 感觉后面几节课的内容跨越太大，需要补充太多的知识点，教授讲得内容跨越较大，一般一节课的内容是书本上的一章节内容，所以看视频比较吃力，需要先预习课本内容后才能够很好的理解教授讲解的知识点。 1. 常见图结构 假设我们有如下图结构： Adjacency Matrix:行和列表示的是节点的位置，A[i,j]表示的第 i 个节点和第 j 个
阅读更多...
hdu 6198 dfs枚举找规律+矩阵乘法

hdu 6198 dfs枚举找规律+矩阵乘法

number number number Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others) Problem Description We define a sequence  F : ⋅   F0=0,F1=1 ; ⋅   Fn=Fn
阅读更多...
PDF 软件如何帮助您编辑、转换和保护文件。

PDF 软件如何帮助您编辑、转换和保护文件。

如何找到最好的 PDF 编辑器。 无论您是在为您的企业寻找更高效的 PDF 解决方案，还是尝试组织和编辑主文档，PDF 编辑器都可以在一个地方提供您需要的所有工具。市面上有很多 PDF 编辑器 — 在决定哪个最适合您时，请考虑这些因素。 1. 确定您的 PDF 文档软件需求。 不同的 PDF 文档软件程序可以具有不同的功能，因此在决定哪个是最适合您的 PDF 软件之前，请花点时间评估您的
阅读更多...
C# double[] 和Matlab数组MWArray[]转换

C# double[] 和Matlab数组MWArray[]转换

C# double[] 转换成MWArray[], 直接赋值就行             MWNumericArray[] ma = new MWNumericArray[4];             double[] dT = new double[] { 0 };             double[] dT1 = new double[] { 0,2 };
阅读更多...
数据流与Bitmap之间相互转换

数据流与Bitmap之间相互转换

把获得的数据流转换成一副图片（Bitmap） 其原理就是把获得倒的数据流序列化到内存中，然后经过加工，在把数据从内存中反序列化出来就行了。 难点就是在如何实现加工。因为Bitmap有一个专有的格式，我们常称这个格式为数据头。加工的过程就是要把这个数据头与我们之前获得的数据流合并起来。（也就是要把这个头加入到我们之前获得的数据流的前面）      那么这个头是
阅读更多...
一些数学经验总结——关于将原一元二次函数增加一些限制条件后最优结果的对比（主要针对公平关切相关的建模）

一些数学经验总结——关于将原一元二次函数增加一些限制条件后最优结果的对比（主要针对公平关切相关的建模）

1.没有分段的情况 原函数为一元二次凹函数（开口向下），如下： 因为要使得其存在正解，必须满足，那么。 上述函数的最优结果为：，。 对应的mathematica代码如下： Clear["Global`*"]f0[x_, a_, b_, c_, d_] := (a*x - b)*(d - c*x);(*(b c+a d)/(2 a c)*)Maximize[{f0[x, a, b,
阅读更多...
线性代数|机器学习-P35距离矩阵和普鲁克问题

线性代数|机器学习-P35距离矩阵和普鲁克问题

文章目录 1. 距离矩阵2. 正交普鲁克问题3. 实例说明 1. 距离矩阵 假设有三个点 x 1 , x 2 , x 3 x_1,x_2,x_3 x1​,x2​,x3​,三个点距离如下： ∣ ∣ x 1 − x 2 ∣ ∣ 2 = 1 , ∣ ∣ x 2 − x 3 ∣ ∣ 2 = 1 , ∣ ∣ x 1 − x 3 ∣ ∣ 2 = 6 \begin{equation} ||x
阅读更多...
高斯平面直角坐标讲解，以及地理坐标转换高斯平面直角坐标

高斯平面直角坐标讲解，以及地理坐标转换高斯平面直角坐标

高斯平面直角坐标系（Gauss-Krüger 坐标系）是基于 高斯-克吕格投影 的一种常见的平面坐标系统，主要用于地理信息系统 (GIS)、测绘和工程等领域。该坐标系将地球表面的经纬度（地理坐标）通过一种投影方式转换为平面直角坐标，以便在二维平面中进行距离、面积和角度的计算。 一 投影原理 高斯平面直角坐标系使用的是 高斯-克吕格投影（Gauss-Krüger Projection），这是 横
阅读更多...
【线性代数】正定矩阵，二次型函数

【线性代数】正定矩阵，二次型函数

本文主要介绍正定矩阵，二次型函数，及其相关的解析证明过程和各个过程的可视化几何解释（深蓝色字体）。 非常喜欢清华大学张颢老师说过的一段话：如果你不能用可视化的方式看到事情的结果，那么你就很难对这个事情有认知，认知就是直觉，解析的东西可以让你理解，但未必能让你形成直觉，因为他太反直觉了。 正定矩阵 定义 给定一个大小为 n×n 的实对称矩阵 A ，若对于任意长度为 n 的非零向量 ，有 恒成
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2