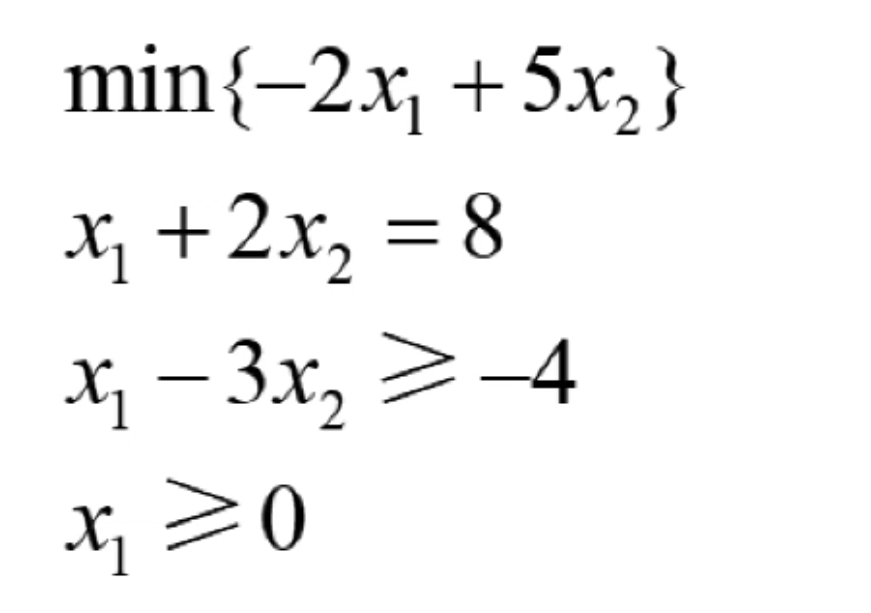标准型专题

腾讯云服务器CVM标准型S8实例CPU内存、网络和存储性能测评

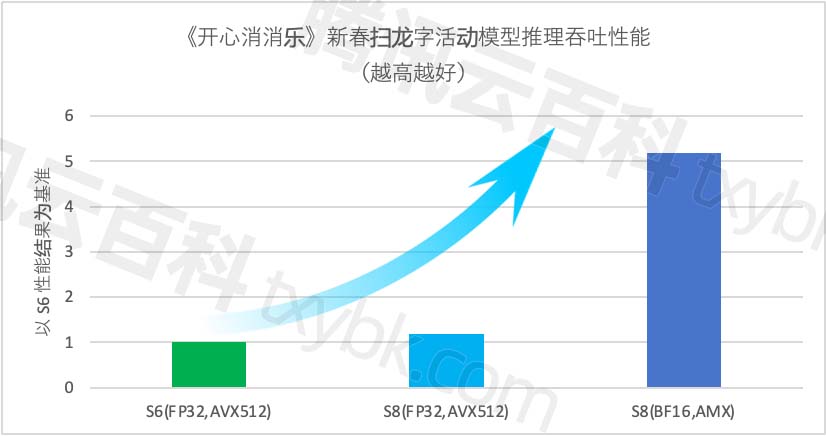
腾讯云第八代云服务器标准型S8实例基于全新优化虚拟化平台，CPU采用Intel Emerald Rapids 全新处理器，睿频3.0GHz，内存采用最新DDR5，默认网络优化，最高内网收发能力达4500万pps，最高内网带宽可支持120Gbps。标准型S8云服务器提供平衡、稳定的计算、内存和网络资源，可胜任众多应用场景。腾讯云百科txybk.com整理腾讯云服务器CVM标准型S8实例CPU型号、处

【矩阵论】11——Jordan标准型——线性变换的特征值与特征向量

本系列文章由Titus_1996 原创，转载请注明出处。文章链接：https://blog.csdn.net/Titus_1996/article/details/83177254 本系列文章使用的教材为《矩阵论》（第二版），杨明，刘先忠编，华中科技大学出版社。定义假设T在某组基{α1，α2，...αn}下的矩阵为A，ξ是T关于λ的特征向量。则有 ξ=(α1，α2，..

若儿当标准型

1. 引言这里略去若尔当块和若尔当矩阵的定义，主要是想谈谈自己对若尔当标准型的理解。我们都知道的简单结论是，对于 n n n阶方阵 A A A，如果 A A A有 n n n个互异的特征值 λ 1 , . . . , λ n \lambda_1,...,\lambda_n λ1,...,λn，那么 A A A是可以对角化的，并且向量空间 V = k e r ( A − λ 1 I )

线性规划的标准型转换

对于任意给定的线性规划的问题，其实其本身可能是不符合线性规划标准型的需求的，但是如果通过一系列的等价变化的话，是可以将该问题转换为标准型的线性规划问题，例如如下的线性规划问题: 添加图片注释，不超过 140 字（可选）给定的线性规划问题存在若干方面不满足最小值，首先就是目标函数是求最小值而不是求最大值，其次就是约束条件中的第2个不等式是大于等于而不是小于等于，最后就是这个问题只要求x

MIT_线性代数笔记：第 28 讲相似矩阵和若尔当标准型

目录正定矩阵 A T A A^TA ATA相似矩阵 Similar matrices特征值互不相同 Distinct eigenvalues重特征值 Repeated eigenvalues 若尔当标准型 Jordan form 本讲介绍相似矩阵，这些内容以及奇异值分解是线性代数最核心的概念。正定矩阵 A T A A^TA ATA 若矩阵 A 满足对任意向量 x≠0

矩阵的相似标准型2

矩阵的相似标准型2 文章目录矩阵的相似标准型24.1 方阵的特征矩阵【定义】方阵的特征矩阵【定理】方阵与其特征矩阵的关系【定理】可通过初等变换相互转化的矩阵等价的推广【定义】矩阵相似【定理】等价与相似间的充要关系 4.2 方阵的三种因子【定义】方阵的行列式因子、不变因子、初等因子【定理】方阵相似 <=> 三种因子相同 4.3 方阵的有理标准型【定义】有理标准型 4.4 方阵的

矩阵的相似标准型2

矩阵的相似标准型2 文章目录矩阵的相似标准型24.1 方阵的特征矩阵【定义】方阵的特征矩阵【定理】方阵与其特征矩阵的关系【定理】可通过初等变换相互转化的矩阵等价的推广【定义】矩阵相似【定理】等价与相似间的充要关系 4.2 方阵的三种因子【定义】方阵的行列式因子、不变因子、初等因子【定理】方阵相似 <=> 三种因子相同 4.3 方阵的有理标准型【定义】有理标准型 4.4 方阵的

腾讯云CVM标准型SA5云服务器AMD EPYC Bergamo处理器

腾讯云服务器标准型SA5实例是最新一代的标准型实例，CPU采用AMD EPYC™ Bergamo全新处理器，采用最新DDR5内存，默认网络优化，最高内网收发能力达4500万pps。腾讯云百科txybk.com分享腾讯云标准型SA5云服务器CPU、内存、网络、性能、使用场景、网络收发包PPS、连接数、队列数和内网标准带宽/突发带宽性能说明：腾讯云标准型SA5云服务器标准型SA5实例是最新一代

腾讯云服务器标准型S5实例CPU性能如何？配置特性说明

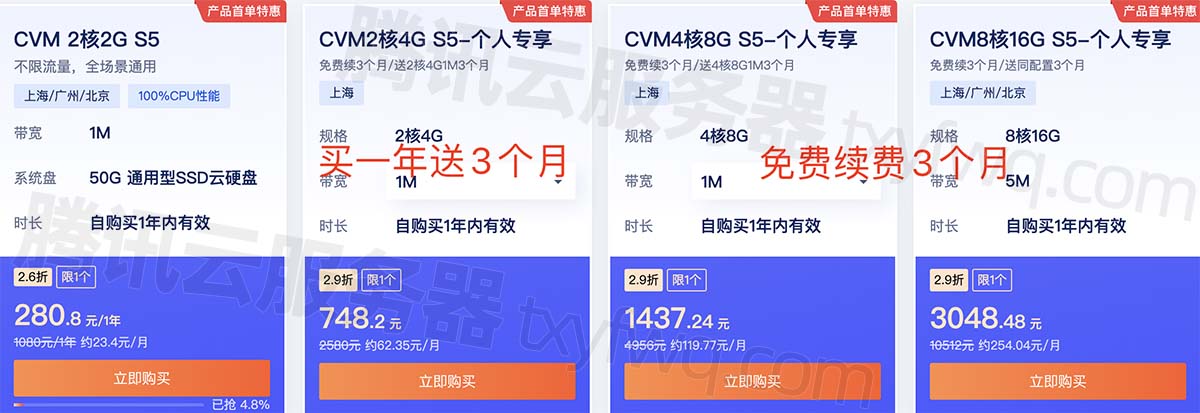
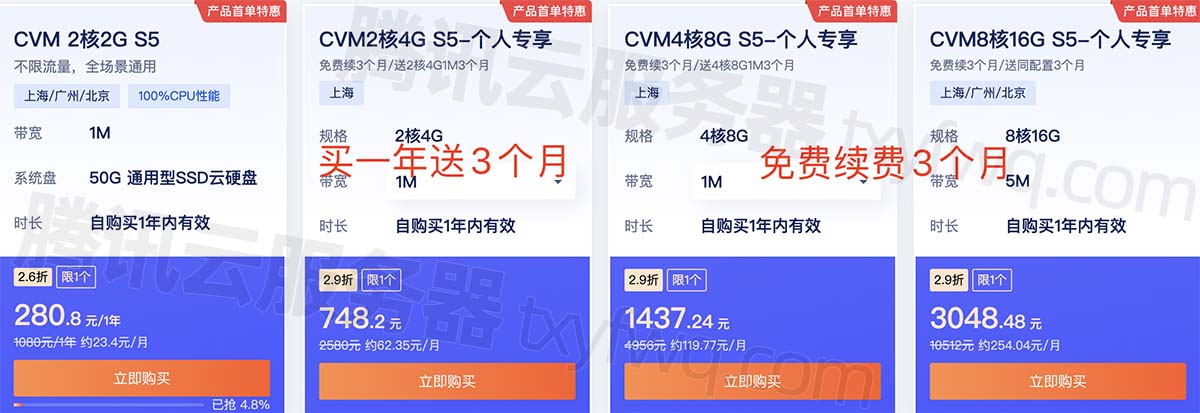
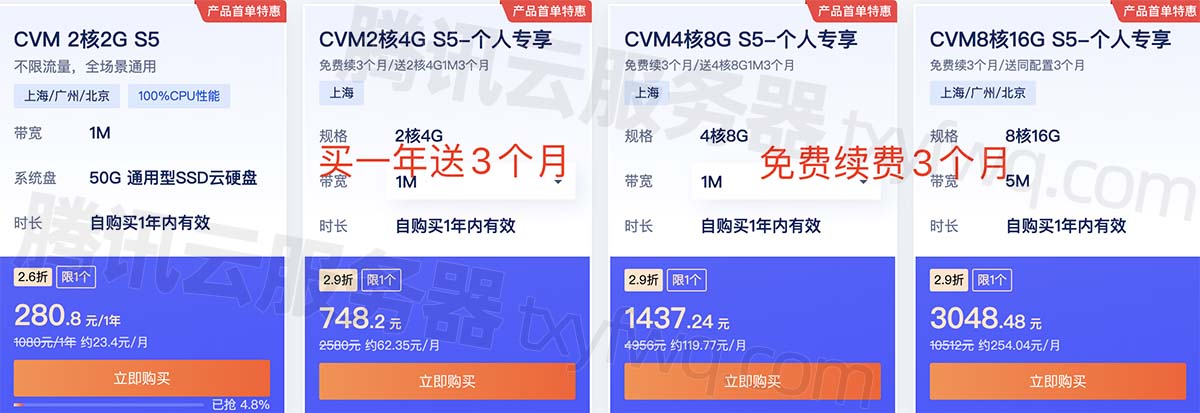
腾讯云服务器CVM标准型S5实例具有稳定的计算性能，CVM 2核2G S5活动优惠价格280.8元一年自带1M带宽，15个月313.2元、2核4G配置748.2元15个月，CPU内存配置还可以选择4核8G、8核16G等配置，公网带宽可选1M、3M、5M或10M，腾讯云百科网txybk.com分享腾讯云服务器CVM标准型S5实例CPU型号主频、性能测评及租用优惠价格表：云服务器CVM标准型S5性

腾讯云服务器标准型S5和CVM标准型S6区别对比_选择攻略

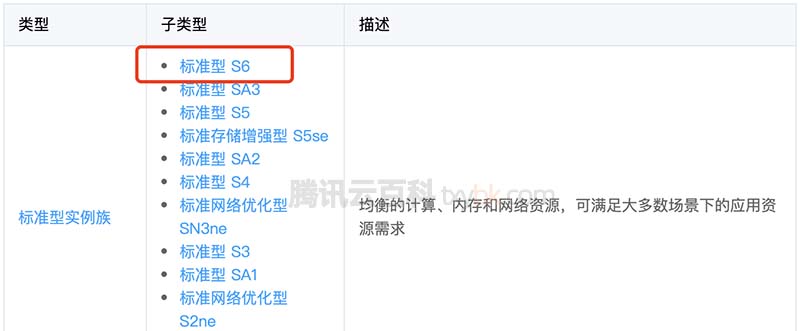
腾讯云服务器CVM标准型S5和S6有什么区别？都是标准型云服务器，标准型S5是次新一代云服务器规格，标准型S6是最新一代的云服务器，S6实例的CPU处理器主频性能要高于S5实例，同CPU内存配置下的标准型S6实例要比S5实例性能更好一些，但是目前标准型S5实例优惠活动较多，腾讯云百科txybk.com来详细说下腾讯云服务器CVM标准型s6和s5的区别对比：腾讯云服务器CVM标准型S5和

腾讯云标准型S5云主机性能评测_CPU内存_带宽系统盘测评

腾讯云服务器CVM标准型S5实例具有稳定的计算性能，CVM 2核2G S5活动优惠价格280.8元一年自带1M带宽，15个月313.2元、2核4G配置748.2元15个月，CPU内存配置还可以选择4核8G、8核16G等配置，公网带宽可选1M、3M、5M或10M，腾讯云百科网txybk.com分享腾讯云服务器CVM标准型S5实例CPU型号主频、性能测评及租用优惠价格表：云服务器CVM标准型S5性

封神测评：腾讯云服务器CVM标准型S5实例CPU内存带宽系统盘

腾讯云服务器CVM标准型S5实例具有稳定的计算性能，CVM 2核2G S5活动优惠价格280.8元一年自带1M带宽，15个月313.2元、2核4G配置748.2元15个月，CPU内存配置还可以选择4核8G、8核16G等配置，公网带宽可选1M、3M、5M或10M，腾讯云百科网txybk.com分享腾讯云服务器CVM标准型S5实例CPU型号主频、性能测评及租用优惠价格表：云服务器CVM标准型S5性

java 仿计算器_Java课程设计----仿Windows标准型计算器

JAVA课程设计仿Windows标准型计算器(By Yanboooooooo) 一、团队介绍：连燕波[组长]：网络1513学生。张文博[组员]：网络1513学生。二、项目git地址三、项目git提交记录截图四、项目主要使用技术 JFrame 五、项目其余特点一个计算器，与Windows附件自带计算器的标准版功能、界面相仿。实现基本的数字运算较传统计算器，使用和携带起来方便。

线性代数（六）| 二次型标准型转换正定二次型正定矩阵

文章目录 1. 二次型化为标准型1.1 正交变换法1.2 配方法 2 . 正定二次型与正定矩阵 1. 二次型化为标准型和第五章有什么样的联系首先上一章我们说过对于对称矩阵，一定存在一个正交矩阵Q，使得$Q^{-1}AQ=B $ B为对角矩阵那么这一章中，我们讲到，二次型写成矩阵后本质上就是一个对称矩阵，而我们想把它变的标准型，不就正好是一个对角矩阵，那么实际上我们的这个

腾讯云服务器标准型S6实例性能评测使用场景及注意事项

腾讯云服务器标准型S6实例新一代腾讯云自研星星海双路服务器，CPU采用主频2.7GHz的Intel Xeon Ice Lake处理器，具有超高网络收发包PPS能力，最高可支持100G内网带宽，腾讯云百科来详细说下腾讯云标准型S6服务器CPU性能、网络带宽、使用场景及注意事项：腾讯云服务器标准型S6实例腾讯云标准型S6服务器是腾讯云推出的新一代标准型实例，具有平衡、稳定的计算、内存和网络资源