代码随想录算法训练营第四十七天 | LeetCode 198. 打家劫舍、213. 打家劫舍 II、337. 打家劫舍 III

本文主要是介绍代码随想录算法训练营第四十七天 | LeetCode 198. 打家劫舍、213. 打家劫舍 II、337. 打家劫舍 III，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

代码随想录算法训练营第四十七天 | LeetCode 198. 打家劫舍、213. 打家劫舍 II、337. 打家劫舍 III

文章链接：打家劫舍打家劫舍 II 打家劫舍 III
视频链接：打家劫舍打家劫舍 II 打家劫舍 III

1. LeetCode 198. 打家劫舍

1.1 思路

我们要去偷钱，但相邻房间不能偷，求最后偷的最大金额。其实我们对于当前房间偷不偷是取决于前一个和前前一个房间的，是一个递推的关系。
dp 数组及其下标的含义：dp[i] 考虑下标 i（包含下标 i），所能偷的最多的金额为 dp[i]，最终结果在 dp[nums.length-1]。注意我们是考虑，考虑的仅仅是遍历的范围，取不取由递推公式决定
递推公式：偷 i 和不偷 i。偷 i 就是只能考虑前前一个房间，即 dp[i-2]+nums[i]，i-2 之前的范围加上 i 就是我们的考虑范围。不偷 i 就是考虑前一个房间，即 dp[i-1]，i-1 之前的范围就是我们的考虑范围。因此递推公式：dp[i]=Math.max（dp[i-2]+nums[i]，dp[i-1]）
dp 数组的初始化：根据递推公式，我们的基础就是 dp[0] 和 dp[1]，dp[0] 就只能是偷 nums[0]，dp[1] 是考虑下标 1 之前的包括下标 1，1 和 0 两个位置取最大值 dp[1]=Math.max（nums[1]，nums[0]），其余下标初始化为 0 即可，不影响
遍历顺序：根据递推公式，就是从前往后比那里的 for（int i=2；i<nums.length；i++）

1.2 代码

// 动态规划
class Solution {public int rob(int[] nums) {if (nums == null || nums.length == 0) return 0;if (nums.length == 1) return nums[0];int[] dp = new int[nums.length];dp[0] = nums[0];dp[1] = Math.max(dp[0], nums[1]);for (int i = 2; i < nums.length; i++) {dp[i] = Math.max(dp[i - 1], dp[i - 2] + nums[i]);}return dp[nums.length - 1];}
}

2. LeetCode 213. 打家劫舍 II

2.1 思路

本题和198. 打家劫舍的区别就是环了，之前是一个线性的数组，本题是把这个数组连成环了，首尾相连，其余的都是相同的。关于连成环首尾怎么取，我们可以分成下面三种情况：
情况 1：首尾都不取，只取中间部分，对于数组是否连成环跟这种情况没有关系，就相当于是线性数组了，直接和我们在198. 打家劫舍处理方式一样
情况 2：考虑首元素不考虑尾元素，就相当于默认数组没有尾元素了，这样对于数组是否连成环也没有关系了
情况 3：不考虑首元素考虑尾元素，就相当于默认数组没有首元素了，这样对于数组是否连成环也没有关系了
关于连成环就是分成了以上三种情况了，但是情况 2 和 3 是包含 1 的。情况 1 是考虑中间部分，情况 2 是考虑首+中间部分，情况 3 是考虑尾+中间部分。注意我们是考虑，不是一定要取，考虑的仅仅是遍历的范围，取不取是由递推公式决定的。因此我们只要求情况 2 的最优解和情况 3 的最优解，两者取最大值即可。我们可以把情况 2 和情况 3 分别传到198. 打家劫舍函数里得到这个线性数组的最大值，两者再取最大值

2.2 代码

class Solution {public int rob(int[] nums) {if (nums == null || nums.length == 0)return 0;int len = nums.length;if (len == 1)return nums[0];return Math.max(robAction(nums, 0, len - 1), robAction(nums, 1, len));}int robAction(int[] nums, int start, int end) {int x = 0, y = 0, z = 0;for (int i = start; i < end; i++) {y = z;z = Math.max(y, x + nums[i]);x = y;}return z;}
}

3. LeetCode 337. 打家劫舍 III

3.1 思路

本题和前面不一样的是我们是在一个二叉树上偷，要求也是相邻节点不能偷，就相当于是树形 dp，因此也用到了之前的递归三部曲
dp 数组及其下标的含义：每个节点只有两个状态，偷与不偷，用一个长度为 2 的 dp 数组就可以表示了，dp[0]=不偷，dp[1]=偷。因为我们在遍历二叉树的过程中是通过递归遍历的，系统栈会保存每一层递归里的参数，每一层递归都有一个长度为 2 的 dp 数组，当前层 dp 数组就是表示当前层所遍历这个节点的状态，dp[0] 就是不偷所得的最大金额，dp[1] 就是偷所得的最大金额。而我们是通过后序遍历从底向上遍历的，最后就是根节点偷与不偷两个状态取最大值
递归函数的参数和返回值：返回值是一个 dp 数组，一维的，长度为 2，参数是 root。我们是通过一个数组来接收这个函数的返回值的。最终是 return Math.max（数组 [0]，数组 [1]）两个状态取最大值
递归函数的终止条件：if（root==null）此时偷与不偷的最大金额都是 0，因为是空节点
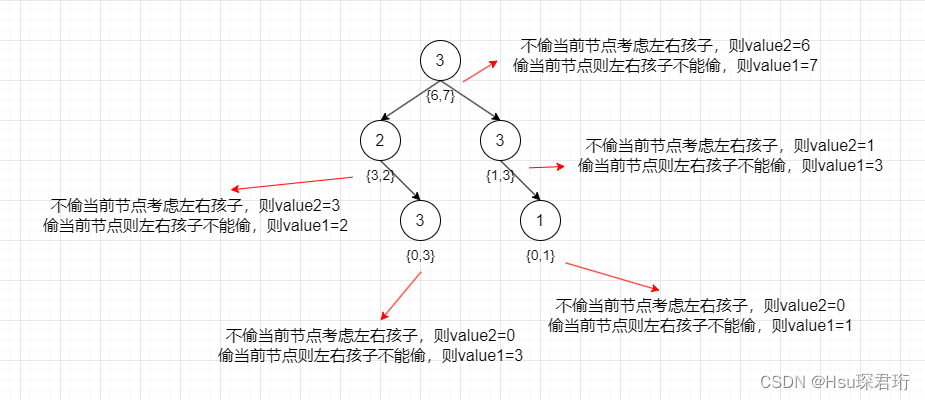
遍历顺序：偷与不偷取一个最大值。偷当前节点，左右孩子就不能偷了 int value1=root.val+leftdp[0]+rightdp[0]。这里的leftdp 和rightdp 就是我们通过后序遍历从底往上推的过程得到的，因此要在上面定义 dp 数组 leftdp 和rightdp 通过递归运算得到 leftdp=递归函数（root.left），rightdp=递归函数（root.right），这样就得到了左右孩子偷与不偷的最大值，因此就能得到当前节点偷与不偷的最大值，当前节点偷了那左右孩子就不能偷 int value1=root.val+leftdp[0]+rightdp[0]，当前节点不偷那左右孩子考虑能偷，偷不偷取决于左右孩子偷与不偷的最大值是什么，dp[0] 和 dp[1] 哪个大就取哪个 int value2=Math.max（leftdp[0]，leftdp[1]）+Math.max（rightdp[0]，rightdp[1]），最终 return value2，value1 组成的数组，注意两个的位置。并且我们上面的逻辑是"左右中"，即后序遍历的逻辑

3.2 代码

// 3.状态标记递归// 执行用时：0 ms , 在所有 Java 提交中击败了 100% 的用户// 不偷：Max(左孩子不偷，左孩子偷) + Max(又孩子不偷，右孩子偷)// root[0] = Math.max(rob(root.left)[0], rob(root.left)[1]) +// Math.max(rob(root.right)[0], rob(root.right)[1])// 偷：左孩子不偷+ 右孩子不偷 + 当前节点偷// root[1] = rob(root.left)[0] + rob(root.right)[0] + root.val;public int rob3(TreeNode root) {int[] res = robAction1(root);return Math.max(res[0], res[1]);}int[] robAction1(TreeNode root) {int res[] = new int[2];if (root == null)return res;int[] left = robAction1(root.left);int[] right = robAction1(root.right);res[0] = Math.max(left[0], left[1]) + Math.max(right[0], right[1]);res[1] = root.val + left[0] + right[0];return res;}
}