R语言回归和主成分PCA 回归交叉验证分析预测城市犯罪率

最近我们被客户要求撰写关于回归和主成分PCA的研究报告，包括一些图形和统计输出。

在本文中，我解释了基本回归，并介绍了主成分分析 (PCA) 使用回归来预测城市中观察到的犯罪率。我还应用 PCA 创建了一个回归模型，用于使用前几个主成分对相同的犯罪数据进行建模。最后，我对两种模型的结果进行了比较，看看哪个表现更好。

 主成分分析PCA降维方法和R语言分析葡萄酒可视化实例

，时长04:30

回归有助于显示因素和因变量之间的关系，它基本上回答了两种类型的问题；1. 吸烟对癌症的影响 2. 未来会发生什么？（例如）三年后的油价。

数据

犯罪学家对惩罚制度对犯罪率的影响感兴趣。已使用汇总数据对此进行了研究。数据集包含以下列：

变量描述
M：  14-24岁的男性在总人口中的百分比
So：  南方州的指标变量
Ed：  25岁或以上人口的平均受教育年限
Po1： 年警察保护的人均支出
Po2： 去年警察保护的人均支出
LF： 14-24岁年龄组的城市男性平民的劳动力参与率
M.F： 每100名女性的男性人数
Pop： 国家人口，以十万计
NW： 非白人在人口中的百分比
U1： 14-24岁城市男性的失业率
U2： 城市男性35-39岁的失业率
财富财富：可转让资产或家庭收入的中值
收入不平等：收入低于中位数一半的家庭的百分比
入狱概率：入狱人数与犯罪人数的比率
时间： 罪犯在首次获释前在国家监狱中服刑的平均时间（月）。
犯罪： 犯罪率：每10万人口中的犯罪数量

我们将数据集导入R环境

read("crim.txt")

检查变量是否正确

head(crim) #所有的变量都是预测因素，只有犯罪是因变量。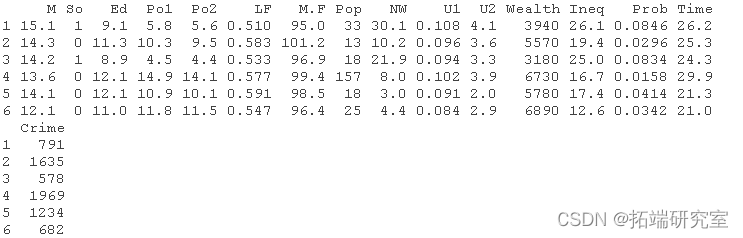

我们正在尝试使用整个数据集来构建回归模型来进行预测。创建简单的回归模型

summary(model)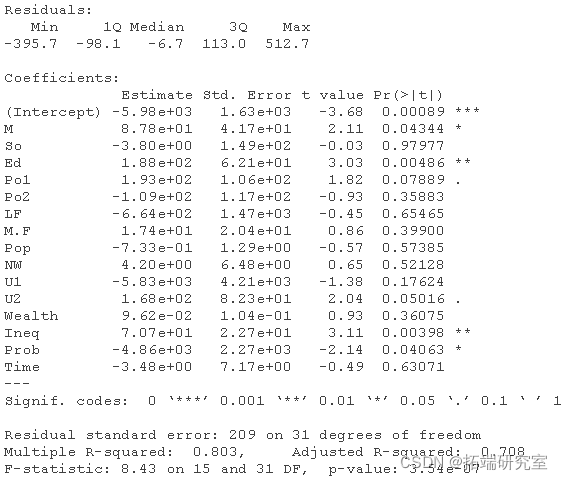

使用数据框架来手动创建我们的数据点测试，然后在测试数据上运行一些预测。

primodl <- predict(mdl, test)primodl 

输出值不到下一个最低城市的犯罪率的一半，所以我将创建第二个模型，观察它的输出并画出比较。

创建第二个模型

sumry(son_mel)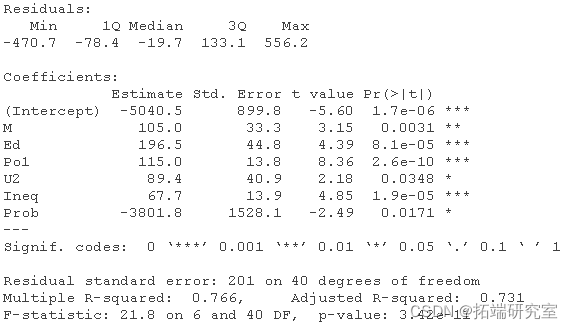

我们现在可以对第二个模型进行预测了

pic_secn_mel<- prict(sed_odel, tst)pic_secn_mel

与第一个模型相比，其结果明显更高。所以，它更合理。

交叉验证

我们可以做一个5折的交叉验证。

cv(se，m=5)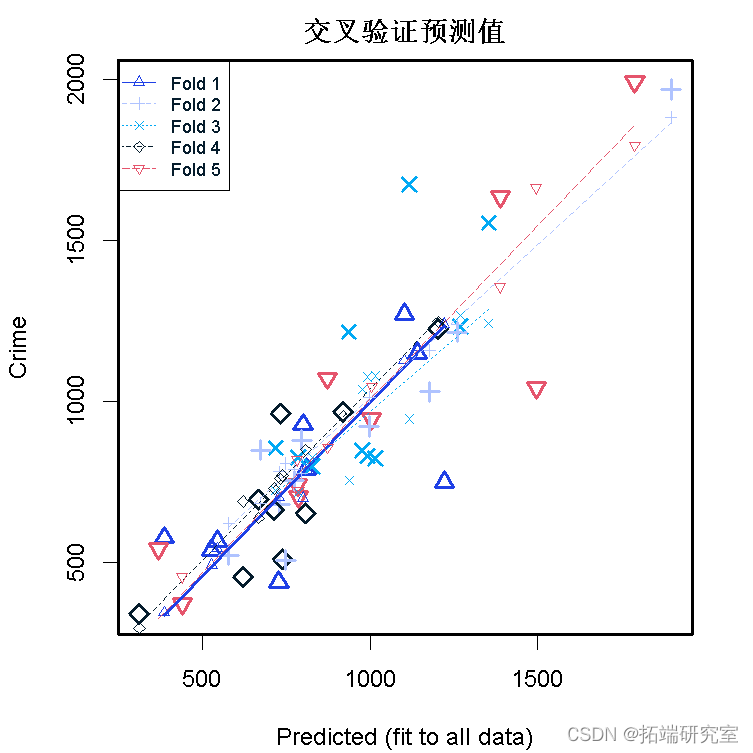

我们可以得到数据和其平均值之间的平方差的总和

 sum((Cm- mean(ui))^2)

我们可以得到模型1、模型2和交叉验证的平方残差之和

SSrl <- sum(res^2)

SSre <- sum(resi^2)

res <- "ms")*nrow

我们也可以计算出3个模型的R平方值

 1 -res/tot

1-res/SS

 1-res/SS

获得的R平方值表明我们的拟合质量很好。对于惩罚性回归，有必要对数据进行标准化，以确保所有的特征都受到同等的惩罚。但在线性回归的情况下，这其实并不重要。它将只是转移截距和系数，但相关关系保持不变。

PCA

PCA是一种用于描述变化的方法，显示数据集中的强相关性，从而使其易于探索和可视化数据。PCA通过以下方式对数据进行转换：（1）去除数据中的相关关系（2）按重要性对坐标进行排序。

我们可以检查crime数据的预测变量之间的相关性。

pairs(srm,c("o",Ed"o"))

对数据集中的所有预测变量应用PCA。请注意，为了获得更准确的PCA结果，需要对这些变量进行标准化。

sumr(pca)
rotan #PCA旋转是特征向量的矩阵
pca

然后，我们可以通过绘制每个主成分的方差来决定在 "前几个 "主成分中使用多少个主成分。

plotpcaye ="ie")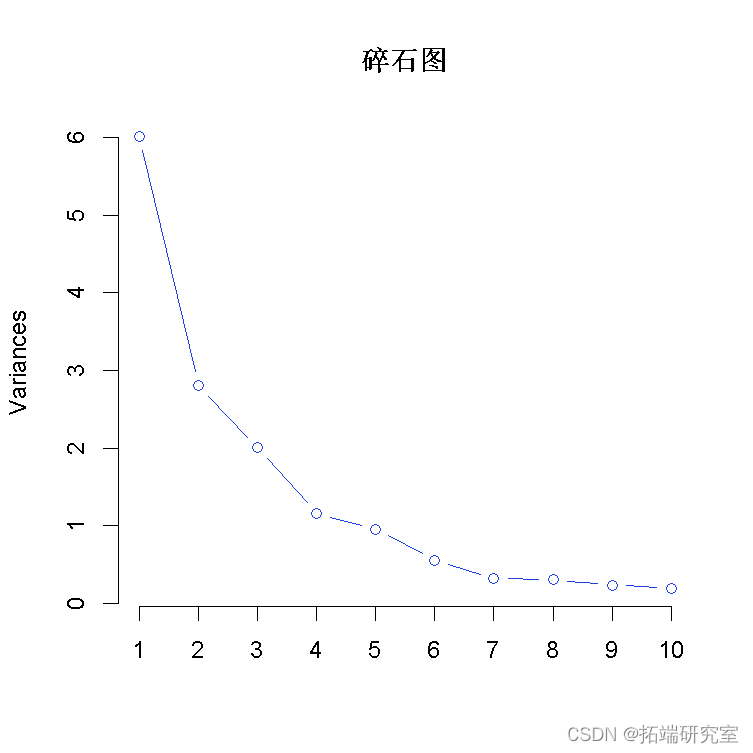

要确定使用多少PC？我们可以尝试使用5个主成分作为开始。

pcax[,1:5]

使用前五个PC，我们可以继续建立一个线性回归模型。

summary(mdPCA)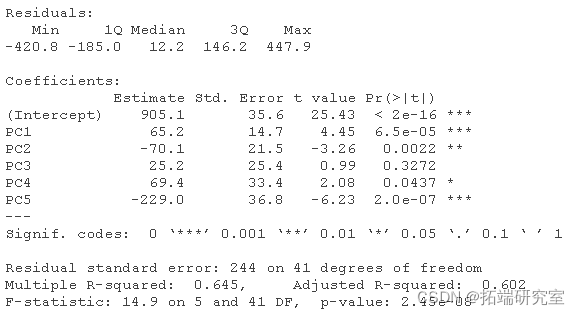

为了根据原始变量重建模型，首先我们从PCA线性回归模型中获得系数，之后通过使用主成分的特征向量将PCA成分系数转化为原始变量的系数。

PCA线性回归的系数

coefficients[1]
coefficients[2:6]beta0 #截距

转换

rot %*% betat(alpha) # 标准化的数据系数

获得未标准化数据的系数。

 ahusl <- ahs / sppy(u[,1:15],sd)ba0cl <- ea0 - sum/sapply(sd))

未标准化数据的系数

 t(alas_sled)be0uced

#我们可以得到我们的未标准化数据的估计值as.marx %*% unscle + beta0aled

最后，为了比较使用PCA的模型和使用回归的模型的质量，我们必须计算R-squared和调整后的R-squared，并将这些数值与前一个模型的数值进行比较。调整后的R平方考虑了模型中预测因子的数量。

Rsquared <- 1 - SSE/SST # R-squared

使用所有变量的无PCA的先前线性回归模型

summary(dlLR)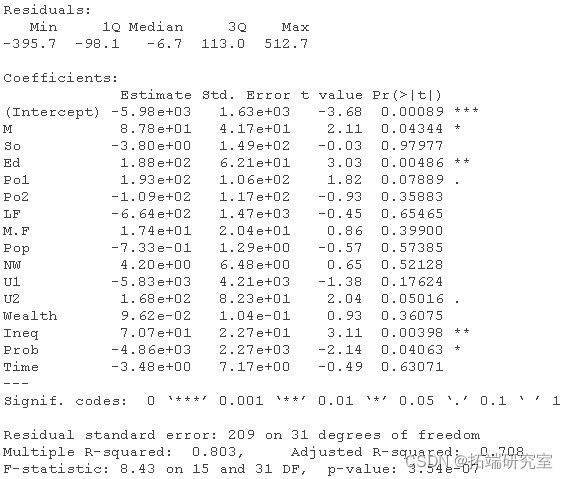

R-squared 和调整后的 R-squared 值都较高，这表明至少对于使用前五个主成分的模型，具有 PCA 的线性回归模型优于没有 PCA 的线性回归模型。为了检查使用不同数量的前 n 个主成分的线性回归模型是否产生了更好的拟合模型，我们可以使用循环并进一步进行交叉验证。

---