本文主要是介绍基于MIMO通信系统的球形译码算法matlab性能仿真,对比PSK检测,SDR检测,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目录
1.算法运行效果图预览
2.算法运行软件版本
3.部分核心程序
4.算法理论概述
5.算法完整程序工程
1.算法运行效果图预览
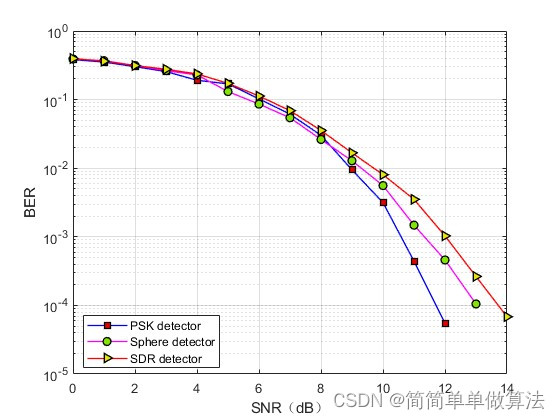
2.算法运行软件版本
MATLAB2022A
3.部分核心程序
................................................................
for i=1:length(SNR) Bit_err(i) = 0;Num_err = 0;Numbers = 0; %误码率累加器 N0 = 10/(10^(SNR(i)/10)); while Num_err <= Times(i)Num_errfprintf('SNR = %f\n', SNR(i));%产生需要发送的随机数Trans_data = round(rand(1,2*data_Numbers)); %QPSKQPSK_IQ = [-1 1]; QPSK_input_I = QPSK_IQ(Trans_data(1:2:end)+1);QPSK_input_Q = QPSK_IQ(Trans_data(2:2:end)+1);Trans_QPSK =(QPSK_input_I + sqrt(-1) * QPSK_input_Q)/sqrt(2);%作为发送信源MIMO_Tx(1,:) = Trans_QPSK;for send_loop = 2:Tm MIMO_Tx(send_loop,:) = MIMO_Tx(1,:); end%信道H_Ray = (randn(Rn,Tm)+sqrt(-1)*randn(Rn,Tm))/sqrt(2);%对信道进一步加入随机干扰H_Ray = abs(H_Ray)+randn(Rn,Tm);%球形译码 decoder算法for k=1:data_NumbersR0 = 1;dR = 0.05;Nr = 10;Nv = 10;rho = 0.99;jj1 = 0;jj2 = 0;y = H_Ray*MIMO_Tx(:,k) + 4*N0*randn(size(H_Ray*MIMO_Tx(:,k)));y = y/max(max(abs(y)));smin = y;
....................................................................smin = smin/max(abs(smin));smin2(:,k) = smin;end%接收MIMO_Rx = smin2 + 2.5*sqrt(N0)*randn(size(smin2))/mod;MIMO_Rx2 = rand(1,Tm)*MIMO_Rx(:,:); %QPSK解调
................................................................end Bit_err(i)=Num_err/(data_Numbers*Numbers);
endfigure;
semilogy(SNR,Bit_err,'o-r');
xlabel('SNR(dB)');
ylabel('BER');
grid on;
save R.mat SNR Bit_err
01_123m4.算法理论概述
球形译码算法(SD)是一种基于多输入多输出(MIMO)通信系统的检测算法。与相移键控(PSK)和软件定义无线电(SDR)相比,它具有更高的频谱效率和可靠性,下面将详细介绍SD算法。
球形译码算法是一种最大似然估计方法,它通过最小化误码率(BER)来估计接收信号的相位和幅度。在MIMO系统中,SD算法可以同时处理多个发送和接收天线,从而提高系统容量和可靠性。
SD算法的核心思想是将接收信号向量视为以原点为球心、以信号强度为半径的球体。在这个球体上,每个接收信号向量都有一个对应的相位和幅度。通过搜索这个球体,找到与每个接收信号向量最近的发送信号向量,从而估计出相位和幅度。
假设发送信号向量X=[x1,x2,...,xm]T,接收信号向量Y=[y1,y2,...,yn]T,其中T表示转置。则MIMO系统可以表示为:
Y=HX+N
其中,H是m×n的信道矩阵,N是噪声矩阵。
在SD算法中,我们假设发送信号向量X是均匀分布的复高斯随机向量,并且与噪声矩阵N相互独立。根据这个假设,我们可以计算出每个接收信号向量的似然函数:
L(x∣y)=exp(-(y−Hx)H(y−Hx)/σ2)
其中,σ2是噪声功率。为了简化计算,我们只考虑噪声矩阵N中的实部和虚部,而忽略它们的相位。这样,我们可以将每个接收信号向量的实部和虚部表示为以原点为球心、以信号强度为半径的半球体。通过搜索这个半球体,我们可以找到与每个接收信号向量最近的发送信号向量,从而估计出相位和幅度。
5.算法完整程序工程
OOOOO
OOO
O
这篇关于基于MIMO通信系统的球形译码算法matlab性能仿真,对比PSK检测,SDR检测的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







