LCR 166.珠宝的最高价值 + 动态规划 + 记忆化搜索 + 递推 + 空间优化

本文主要是介绍LCR 166.珠宝的最高价值 + 动态规划 + 记忆化搜索 + 递推 + 空间优化，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

LCR 166. 珠宝的最高价值 - 力扣（LeetCode）

现有一个记作二维矩阵 frame 的珠宝架，其中 frame[i][j] 为该位置珠宝的价值。拿取珠宝的规则为：

只能从架子的左上角开始拿珠宝
每次可以移动到右侧或下侧的相邻位置
到达珠宝架子的右下角时，停止拿取

注意：珠宝的价值都是大于 0 的。除非这个架子上没有任何珠宝，比如 frame = [[0]]。

（1）递归

定义：dfs(i,j) 表示从左上角 到 (i,j) 的最大价值和

寻找子问题，把大问题变成小问题，分类讨论如何到达(i,j):

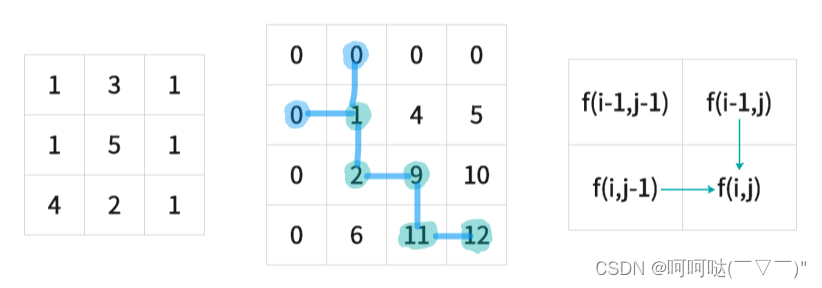
若从左边过来，则 dfs(i,j) = dfs(i,j-1)+grid[i][j];
若从上边过来，则 dfs(i,j) = dfs(i-1,j)+grid[i][j];

取这两个分类情况的最大值：dfs(i,j) = max(dfs(i,j-1),dfs(i-1,j))+grid[i][j];

递归边界：当 i < 0 或 j < 0 时，返回 0，因为出界是没有价值的，也就是
- dfs(-1,j)=0,dfs(i,-1)=0
递归入口：
- dfs(m-1,n-1)

class Solution {
public:// 递归 超时！！！int jewelleryValue(vector<vector<int>>& grid) {  int n=grid.size(),m=grid[0].size();function<int(int,int)> dfs = [&](int i,int j) -> int{if(i<0 || j<0) return 0;return max(dfs(i-1,j),dfs(i,j-1))+grid[i][j];};return dfs(n-1,m-1);}
};

时间复杂度： $O(2^{n+m})$
空间复杂度： $O(n+m)$

>>复杂度分析

其中 n 和 m 分别为 grid 的行数和列数。搜索树可以近似为一棵二叉树，树高为O(n+m)。也意味着从 grid 左上角到右下角经过的格子数，所以节点个数为 $O(2^{n+m})$
递归需要 O(n+m) 的栈空间

（2）递归搜索 + 保存计算结果 = 记忆化搜索

对于 $dfs(3,3)$ ，「先左再上」和「先上再左」，都会调用 $dfs(2,2)$ 。同理，那么整个递归中有大量重复递归调用（递归入参相同）
因为递归函数无副作用，同样的入参无论计算多少次，都是一样的结果，可用记忆化搜索来优化

>>注意事项

如果 grid 中有 0，memo 数组初始化成 -1
如果 grid 中有负数，memo 数组可以初始化成很大或者很小的数，如：INT_MAX,INT_MIN

class Solution {
public:// 记忆化搜索int jewelleryValue(vector<vector<int>>& grid) {  int n=grid.size(),m=grid[0].size(),memo[n][m];// vector<vector<int>> memo(n+1,vector<int>(m+1,-1));memset(memo,0,sizeof(memo));function<int(int,int)> dfs = [&](int i,int j) -> int{if(i<0 || j<0) return 0;int &res = memo[i][j];if(res) return res;// grid[i][j] 都是正数，记忆化的 memo[i][j] 必然为正数return res=max(dfs(i-1,j),dfs(i,j-1))+grid[i][j];};return dfs(n-1,m-1);}
};

class Solution {
public:// 记忆化搜索int jewelleryValue(vector<vector<int>>& grid) {  int n=grid.size(),m=grid[0].size(),memo[n+1][m+1];// vector<vector<int>> memo(n+1,vector<int>(m+1,-1));memset(memo, -1, sizeof(memo));function<int(int,int)> dfs = [&](int i,int j) -> int{if(i<0 || j<0) return 0;int &res = memo[i][j];if(res != -1) return res;return res=max(dfs(i-1,j),dfs(i,j-1))+grid[i][j];};return dfs(n-1,m-1);}
};

时间复杂度： $O(nm)$
空间复杂度： $O(nm)$

>>复杂度分析

由于每个状态只会计算一次，状态个数为O(nm)，单个状态的计算时间为O(1)，所以

动态规划的时间复杂度 = 状态个数 x 单个状态的计算时间
O(nm) = O(nm) x O(1)

（3）1:1 翻译成递推

去掉递归中的「递」，只保留「归」的部分，即自底向上计算

翻译步骤：

dfs 改成 f 数组
递归改成循环（每个参数都对应一层循环）
递归边界改成 f 数组的初始值

$dfs(i,j) = max(dfs(i,j-1),dfs(i-1,j))+grid[i][j];$

↓

$f[i][j] = max(f[i][j-1],f[i-1][j])+grid[i][j];$

存在问题(O_O)?：当 i = 0,j = 0 时，这种定义方式没有状态能表示边界（出界的情况）

解决方案：在 f 数组的上边和左边各加一排，

f[i] -> f[i+1],f[i-1] -> f[i],f[j] -> f[j+1],f[j-1] -> f[j]
$f[i+1][j+1] = max(f[i+1][j],f[i][j+1])+grid[i][j];$

初始化：根据 dfs(i,-1) = 0 和 dfs(-1,j) = 0 翻译，f[i][0]=0,f[0][j]=0

返回最终结果：根据 dfs(m-1,n-1) 翻译， f[m][n]

① f[i+1][j+1] = max(f[i+1][j],f[i][j+1])+grid[i][j]; （推荐）

class Solution {
public: // 递推int jewelleryValue(vector<vector<int>>& grid) {  int n=grid.size(),m=grid[0].size(),f[n+1][m+1];// vector<vector<int>> f(n+1,vector<int>(m+1,0));memset(f,0,sizeof(f));for(int i=0;i<n;i++) {for(int j=0;j<m;j++) {f[i+1][j+1] = max(f[i][j+1],f[i+1][j])+grid[i][j];}}return f[n][m];}
};

② f[i][j] = max(f[i][j-1],f[i-1][j])+grid[i][j];

class Solution {
public:// 递推int jewelleryValue(vector<vector<int>>& grid) {  int n=grid.size(),m=grid[0].size();vector<vector<int>> f(n,vector<int>(m,0));f[0][0]=grid[0][0];for(int i=0;i<n;i++) {for(int j=0;j<m;j++) {if(i==0 && j>=1) f[0][j] = f[0][j-1] + grid[0][j];if(j==0 && i>=1) f[i][0] = f[i-1][0] + grid[i][0];if(i>=1 && j>=1) f[i][j] = max(f[i-1][j],f[i][j-1])+grid[i][j];}}return f[n-1][m-1];}
};

时间复杂度： $O(nm)$
空间复杂度： $O(nm)$

（4）空间优化

方法一：两个数组，滚动数组

class Solution {
public: // 递推 + 空间优化int jewelleryValue(vector<vector<int>>& grid) {  int n=grid.size(),m=grid[0].size(),f[2][m+1];// vector<vector<int>> f(2,vector<int>(m+1,0));memset(f,0,sizeof(f));for(int i=0;i<n;i++) {for(int j=0;j<m;j++) {f[(i+1)%2][j+1] = max(f[i%2][j+1],f[(i+1)%2][j])+grid[i][j];}}return f[n%2][m];}
};

时间复杂度： $O(nm)$
空间复杂度： $O(m)$

方法二：一个数组，滚动数组

本题的转移方程类似完全背包，故采用正序遍历

class Solution {
public:// 递推 + 空间优化int jewelleryValue(vector<vector<int>>& grid) {  int n=grid.size(),m=grid[0].size(),f[m+1];// vector<int>f(m+1,0);memset(f,0,sizeof(f));for(int i=0;i<n;i++) {for(int j=0;j<m;j++) {f[j+1] = max(f[j+1],f[j])+grid[i][j];}}return f[m];}
};

时间复杂度： $O(nm)$
空间复杂度： $O(m)$

方法三：原地修改

class Solution {
public:// 递推 + 空间优化 + 原地修改int jewelleryValue(vector<vector<int>>& frame) {  int n=frame.size(),m=frame[0].size();for(int i=0;i<n;i++) {for(int j=0;j<m;j++) {if(i==0 && j>=1) frame[0][j] = frame[0][j-1] + frame[0][j] ;if(j==0 && i>=1) frame[i][0] = frame[i-1][0] + frame[i][0];if(i>=1 && j>=1) frame[i][j] = max(frame[i-1][j],frame[i][j-1])+frame[i][j];}}return frame[n-1][m-1];}
};

时间复杂度： $O(nm)$
空间复杂度： $O(1)$

参考和推荐文章：

LCR 166. 珠宝的最高价值 - 力扣（LeetCode）https://leetcode.cn/problems/li-wu-de-zui-da-jie-zhi-lcof/solutions/2153802/jiao-ni-yi-bu-bu-si-kao-dpcong-hui-su-da-epvl/