本文主要是介绍《Predict then Propagate: Graph Neural Networks meet Personalized PageRank》论文阅读笔记,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
文章:Predict then Propagate: Graph Neural Networks meet Personalized PageRank
出处:ICLR 2019
作者:Johannes Klicpera, Aleksandar Bojchevski & Stephan Gunnemann
机构:Technical University of Munich, Germany
1. 背景
传统GCN在节点分类中达到了不错的效果,但只能在将层数限制在2-3层,加深层数会导致两个问题:
- 出现过平滑现象:即最后所有节点趋向同一个值。
- 随着层数的加深,参数量也呈指数级增长,同时所利用的邻域的大小难以扩展。
因此提出:
使用基于图卷积网络GCN与PageRank之间的关系来推导基于个性化PageRank的改进传播方案。利用这种传播程序来构建一个简单的模型,神经网络预测的个性化传播模型(PPNP)及其快速逼近模型APPNP。
2. introduction
链路预测,图分类和半监督节点分类等可以利用图上的深度学习算法。 例如:
无监督方法:节点嵌入方法使用随机游走或矩阵分解直接训练单个节点嵌入,通常不使用节点特征并且通常以无监督的方式使用,即不利用节点类。
有监督方法:频谱图卷积神经网络,消息传递(或邻居聚合)算法,RNN神经网络,注意力机制等。
所有这些方法仅对每个节点使用非常有限的邻域信息。希望有更大的邻域来为模型提供更多信息,尤其是对于外围或稀疏标记设置中的节点。
这些算法使用的邻域大小(即它们的范围)并不是微不足道的,因为该方案中的邻域聚合本质上是 Laplacian smoothing 的一种,并且太多层会导致过度smoothing。
根据图卷积网络(GCN)的消息传递算法与随机游走之间的关系,可以看出随着层数的增加,GCN会收敛到该随机游走的极限分布。 极限分布是整个图的一个属性,没有考虑随机游走的起始(根)节点。因此,不适合描述根节点的邻居。因此,GCN的性能必然会因大量层(或聚合/传播步骤)而下降。
为了解决这个问题,作者根据极限分布与PageRank之间的内在联系提出了一种新的算法:PPNP和APPNP。
- 该算法利用从个性化PageRank派生的传播方案。
- 该算法增加了传回根节点的机会,从而确保PageRank分数对每个根节点的局部邻域进行编码。
- 传播方案使我们能够平衡以下方面的需求:保留局部性(即,保持靠近根节点以避免过度平滑),以及平衡来自大型社区的信息的需求。 我们表明,这种传播方案允许使用更多(实际上是无限多个)传播步骤,而不会导致过度平滑。
- 与大多数竞争模型相比,我们的模型可实现最新的结果,同时需要更少的参数和更少的训练时间,并且计算复杂度与边沿数量呈线性关系。
3. 图卷积网络(GCN)
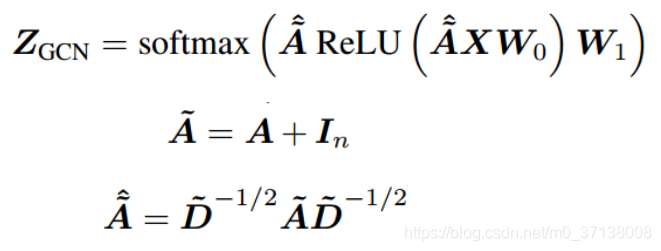
存在的缺陷:
- 如果使用了太多的层,则通过求平均的聚合会导致过度平滑。 因此,它失去了对 local neighborhood的关注。
- 使用更大的邻域必然会增加神经网络的可学习参数的深度和数量。
4. 从消息传递到个性化PageRank
原始的PageRank算法
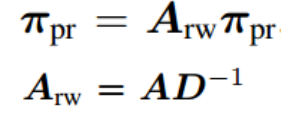
考虑根节点的信息和传播方式的个性化PageRank算法


5. 从个性化PageRank到神经网络预测的个性化传播(PPNP)
为了将上述影响力分数用于半监督分类,作者根据每个节点的自身特征生成预测,然后通过个性化PageRank方案传播它们,以生成最终预测。
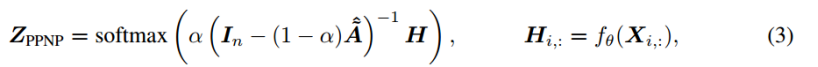

PPNP从传播方案中分离出了用于生成预测的神经网络。
这种分离解决了上面提到的第二个问题:神经网络的深度现在完全独立于传播算法。
个性化PageRank甚至可以有效地使用无限多个邻域聚合层,这在传统消息传递框架中显然是不可能的。
分离使我们可以灵活地使用任何方法来生成预测,例如用于图像图形的深层卷积神经网络。

6. 神经网络预测的近似个性化传播(APPNP)
APPNP通过通过幂迭代逼近主题敏感的PageRank来实现线性计算复杂性。 虽然PageRank的功效迭代与常规的随机游走相关,但与主题相关的PageRank的功效迭代与重新启动的随机游走有关。 因此,主题敏感的PageRank变体的每次幂迭代(随机遍历/传播)步骤都可以通过以下式子实现:
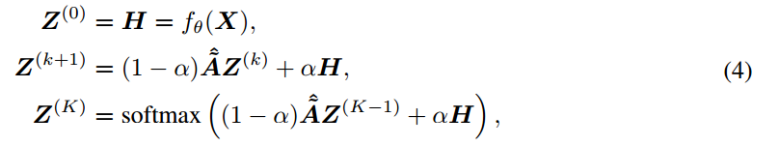

在PPNP和APPNP中,可以通过传送概率α来调整影响每个节点的邻域的大小。 可以自由地使我们能够针对不同类型的网络调整模型。
7. 实验
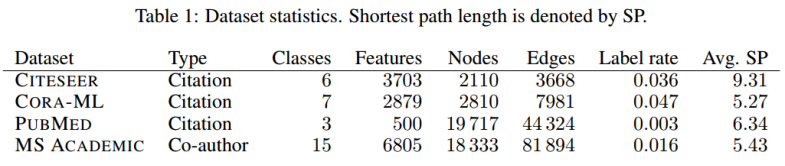
数据集
实验效果


。。。。。。
8. Conclusion
- 提出了神经网络预测的个性化传播(PPNP)及其快速逼近APPNP。
- 通过考虑GCN和PageRank之间的关系并将其扩展到个性化PageRank来推导此模型。
- 这个简单的模型将预测和传播解耦,并解决了许多消息传递模型中固有的有限范围问题,而无需引入任何其他参数。
- 它使用来自较大的可调整的(通过传送概率α)邻域的信息对每个节点进行分类。
- 该模型具有高效的计算能力,并且优于迄今为止针对类似GCN的模型所做的最彻底研究中针对多张图进行半监督分类的几种最新方法。
- 对于以后的工作,将PPNP与使用的更复杂的神经网络相结合会很有趣。在计算机视觉或自然语言处理中。
这篇关于《Predict then Propagate: Graph Neural Networks meet Personalized PageRank》论文阅读笔记的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








