Deterministic Policy Gradient Algorithms

本文研究具有连续动作的确定性策略梯度算法。确定性策略梯度有一种特别吸引人的形式:它是行动-价值函数的期望梯度。这种简单的形式意味着确定性策略梯度的估计比一般的随机政策梯度的估计要有效得多。为了确保充分的探索，我们引入了一种非策略行为-批评算法，该算法从探索行为策略中学习确定的目标策略。我们证明了确定性策略梯度算法在高维行为空间中可以显著优于随机算法。

背景：

1）策略梯度算法通常通过对该随机策略进行抽样，并向更大的累积回报方向调整策略参数。本文考虑确定性策略a = μ θ(s)。

2）使用确定性策略梯度推导出一种off-policy actor - critic算法，该算法使用可微函数逼近器估计动作价值函数，然后沿着近似动作价值梯度的方向更新策略参数。

3）此外，该算法不需要比之前的方法更多的计算:每次更新的计算成本与动作维度和策略参数数量是线性的。

3. Gradients of Deterministic Policies

 通过应用链式法则，我们可以看到策略改进可以分解为动作值相对于动作的梯度，以及策略相对于策略参数的梯度

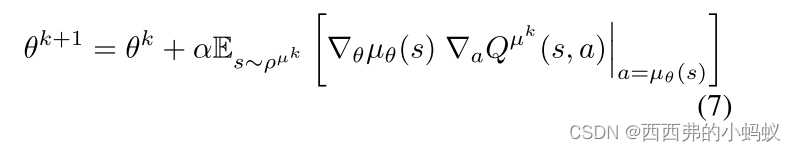
按照惯例，∇θµθ(s)是一个雅可比矩阵，其中每一列是策略的第一个动作维度相对于策略参数θ的梯度∇θ[µθ(s)]d。

 3.2. Deterministic Policy Gradient Theorem

 4. Deterministic Actor-Critic Algorithms

我们现在使用确定性策略梯度定理来推导on-policy and off-policy actor-critic algorithms。我们从最简单的例子开始——policy 更新，使用一个简单的Sarsa批评家——以便尽可能清楚地说明想法。然后考虑policy 外的情况，这次使用一个简单的q学习评论器来说明关键思想。这些简单的算法在实践中可能存在收敛性问题，这一方面是由于函数逼近器引入的偏差，另一方面是由于非策略学习引起的不稳定性。然后转向使用兼容函数逼近和梯度时间差分学习的更原则性的方法。

4.1. On-Policy Deterministic Actor-Critic 

批评者对行为价值函数进行估计，而行动者则提升行为价值函数的梯度。具体而言，行动者通过方程9的随机梯度上升来调整确定性策略µθ(s)的参数θ 

 例如，在下面的确定性行动者-批评者算法中，批评者使用Sarsa更新来估计行动价值函数(Sutton and Barto, 1998)，

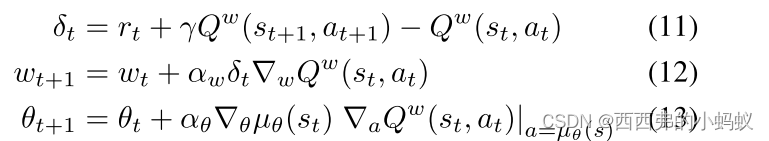
 4.2. Off-Policy Deterministic Actor-Critic

我们现在考虑从由任意随机行为策略π(s, a)生成的轨迹中学习确定的目标策略μ θ(s)的off-policy 。像以前一样，我们将性能目标修改为目标策略的值函数，在行为策略的状态分布上进行平均

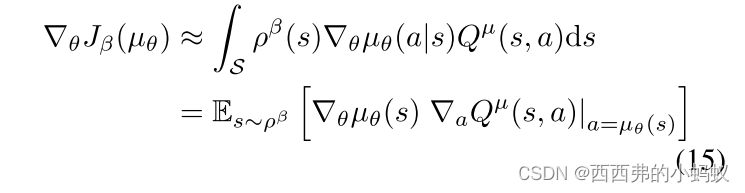
我们注意到，stochastic off-policy actor-critic algorithms通常对行为者和评价者都使用重要性采样(Degris等人，2012b)。然而，由于确定性策略梯度消除了对动作的积分，我们可以避免对actor进行重要性采样;通过使用Qlearning，我们可以避免在评价器中进行重要性采样 

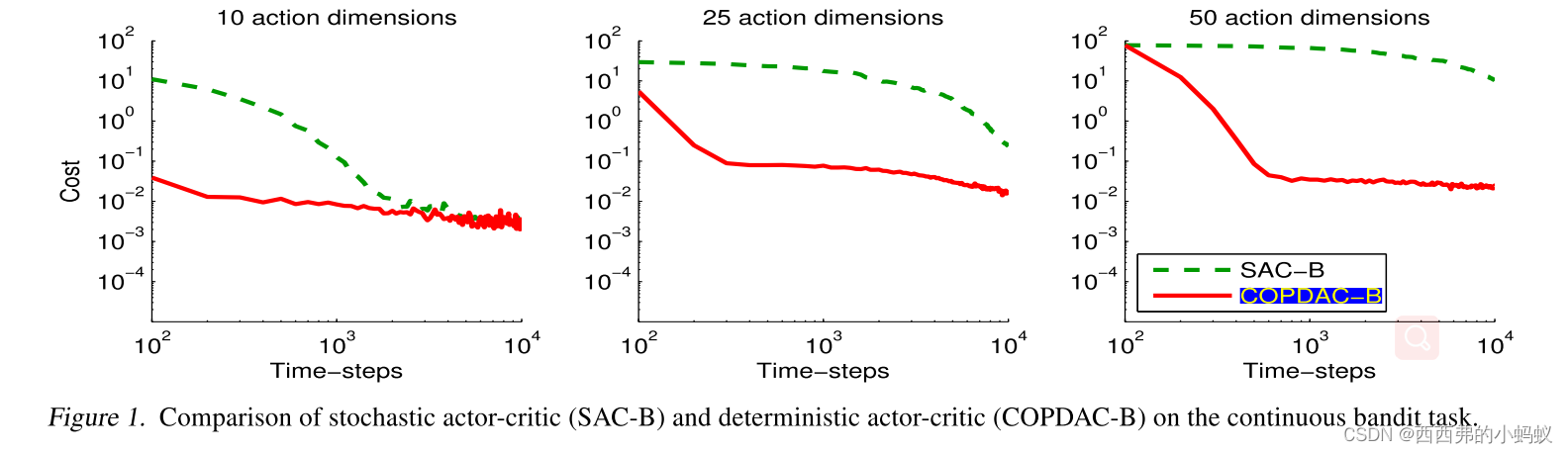
 7. Conclusion

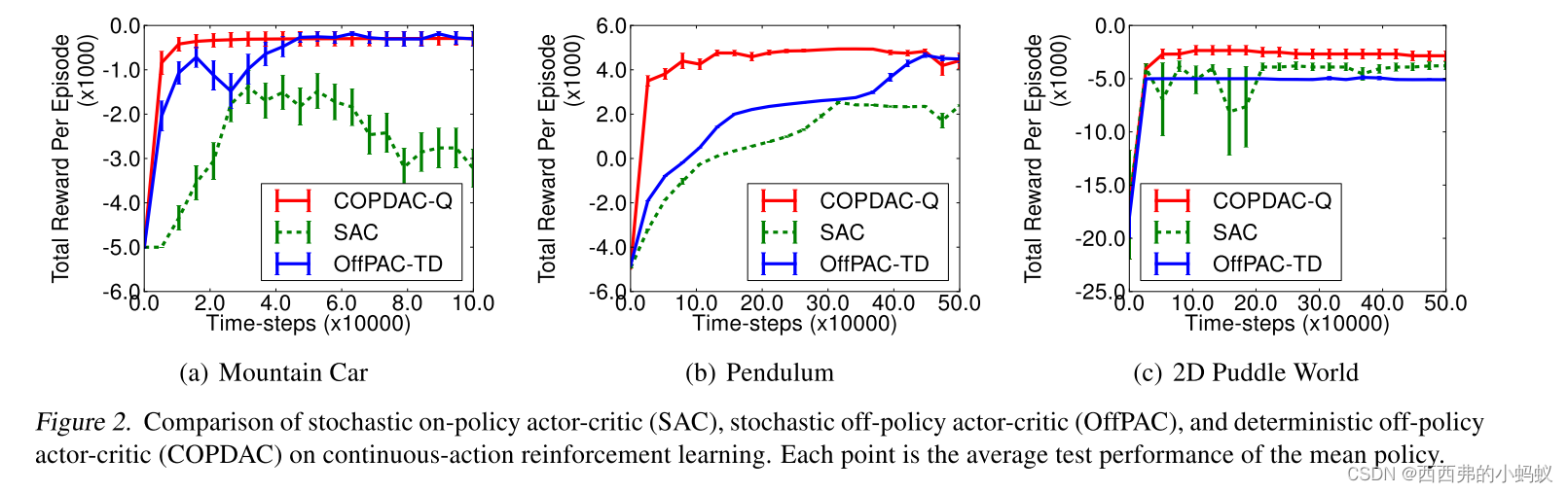
我们提出了一个确定性策略梯度算法的框架。这些梯度可以比随机对应的梯度更有效地估计，避免了行动空间上有问题的积分。在实践中，确定性的actor-critic在具有50个连续动作维度的bandit中明显优于随机对应的几个数量级，并解决了具有20个连续动作维度和50个状态维度的挑战性强化学习问题。