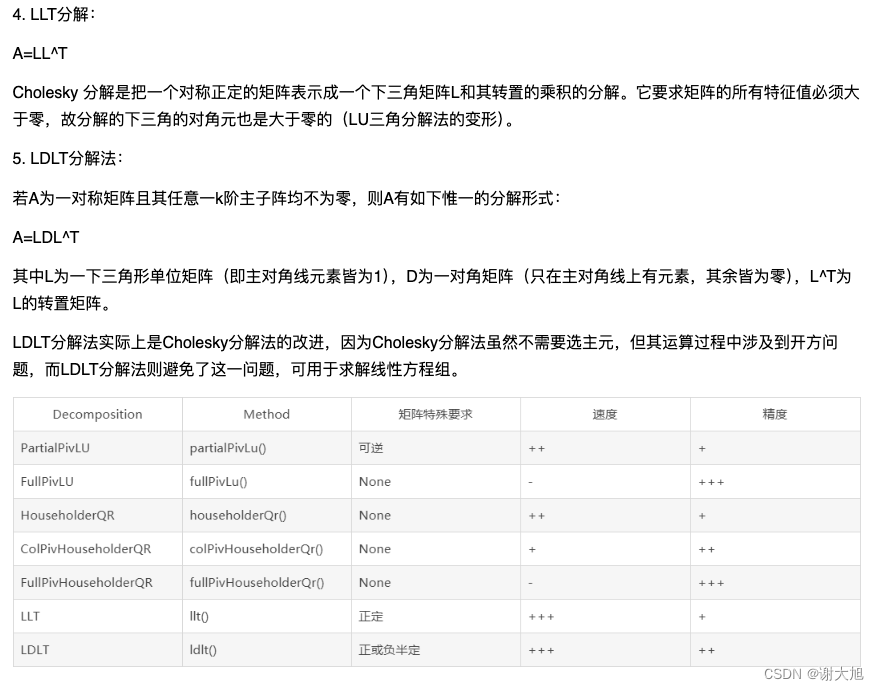
本文主要是介绍线性方程组QAQ,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
-1.序言
更佳阅读
- 想了解更多关于数论的内容,可戳这里
说到线性方程组,大家第一反应大概就是高斯消元,本文将对其详细讲解并配合例题与相关方法为您呈现。
本文因图文并茂有较多配图且讲解详细较多,再过多的放置代码会引起文章的冗长以及阅读的不适,故只将模板放在上面。
另特别鸣谢@command_block,原因见下图:

(灵感所在),这是出处
0、由来
遇到形如:
{ a 11 x 1 + a 12 x 2 + . . . + a 1 n x n = b 1 a 21 x 1 + a 22 x 2 + . . . + a 2 n x n = b 2 . . . . . . . . . a n 1 x 1 + a n 2 x 2 + . . . + a n n x n = b n \begin{cases}a_{11}x_1+a_{12}x_2+...+a_{1n}x_n=b_1\\a_{21}x_1+a_{22}x_2+...+a_{2n}x_n=b_2\\. . .\\. . .\\. . .\\a_{n1}x_1+a_{n2}x_2+...+a_{nn}x_n=b_n\end{cases} ⎩⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎧a11x1+a12x2+...+a1nxn=b1a21x1+a22x2+...+a2nxn=b2.........an1x1+an2x2+...+annxn=bn
这样的方程组,你会怎么解呢?
如果是在数学领域中,可能这样的方程组中方程的个数是屈指可数的,这样就特别简单,一通乱搞就出来了。
但是如果在OI领域遇到这类问题呢?我们发现,计算机中必须由固定的算法,才能实现某一问题,而人脑能进行综合性的思考,但是却无法将大脑中的神经元活动表述到程序中,这是人脑与电脑的区别,也就由此诞生了各种解线性方程组的方法。
说到这里,我想起了一本著名的书:计算机与人脑。冯诺依曼写的,有兴趣者可以自行购买阅读也能普及一些历史
这种线性的方程组在工程中也运用广泛,这种模型中:
-
未知量较多
-
方程个数不同
而在考虑解方程时,要考虑:
-
是否有解?
-
如果有解,是否唯一?
-
如果不唯一,解有什么规律与结构?
由此,线性方程组的解决方法就显得尤为重要。
下面就来介绍一下两种常用的方法及相关例题
1、高斯消元
插播一些历史知识:
该方法以数学家高斯命名,由拉布扎比.伊丁特改进,发表于法国但最早出现于中国古籍《九章算术》,成书于约公元前150年。
自豪ingQAQ
高斯:
为德国著名数学家、物理学家、天文学家、几何学家,大地测量学家。享有“数学王子”的美誉,真的是多才多艺,著名的“自然数1~100的求和问题”就是他9岁时计算出来的,虽然可能现在对我们来说轻而易举,但是的确体现了他那时的创新精神,为日后的研究打下了坚实的基础。
这种是大家比较耳熟能详的解法了。
那么,这种解法的核心思想是什么呢?
我们先来构想一下,什么样子的线性方程式我们用电脑也能写出解法?
显然,我们如果从某一个式子开始,每一个式子都能得到一个未知数的解,而得到了这个未知数的解,又能代入另一个方程,再得到一个未知数的解。
以此类推。
没错就是本萌新最擅长的无脑递推
总结一下,就是一个“三角形分割”《----(自己瞎起的名字)
还是拿上面那个普遍形式:
{ a 11 x 1 + a 12 x 2 + . . . + a 1 n x n = b 1 a 21 x 1 + a 22 x 2 + . . . + a 2 n x n = b 2 . . . . . . . . . a n 1 x 1 + a n 2 x 2 + . . . + a n n x n = b n \begin{cases}a_{11}x_1+a_{12}x_2+...+a_{1n}x_n=b_1\\a_{21}x_1+a_{22}x_2+...+a_{2n}x_n=b_2\\. . .\\. . .\\. . .\\a_{n1}x_1+a_{n2}x_2+...+a_{nn}x_n=b_n\end{cases} ⎩⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎧a11x1+a12x2+...+a1nxn=b1a21x1+a22x2+...+a2nxn=b2.........an1x1+an2x2+...+annxn=bn
但是为了观察方便,我们假设一个三行四列的式子:(真香)
{ x 1 + 3 x 2 + 4 x 3 = 5 x 1 + 4 x 2 + 7 x 3 = 3 9 x 1 + 3 x 2 + 2 x 3 = 2 \begin{cases}x_1+3x_2+4x_3=5\\x_1+4x_2+7x_3=3\\9x_1+3x_2+2x_3=2\end{cases} ⎩⎪⎨⎪⎧x1+3x2+4x3=5x1+4x2+7x3=39x1+3x2+2x3=2
此时把系数写到矩阵里:(没学过矩阵也没关系,就当成一个表示就行啦)
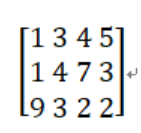
其实就是高斯消元模板题的样例
第一步:对左侧的系数进行消元,即对:

进行向“三角形分割”的转换
即目标状态为

此时,我们设标红的1为主元,对照目标状态可知,标绿的1和9需要化0
所以我们只需要将第二行整体减去第一行,就实现了将绿1化0
那么9如何转化呢?
此时就对应的整体减去9倍的第一行就行(可能会有更简便的系数化0法,但是我们要给计算机设计一个统一的算法才能实现)
于是就得到了:

然后再以绿1为主元,现在我们需要将-24化为0
于是将第三行整体减去 − 24 -24 −24倍第二行(其实相当于加24倍)

Q:这里不会把之前第一列化好的0给冲掉吗?
A:显然,在上一步已经保证第一列除主元外系数皆为0,所以不会出现上述情况
Q:万一上面那个绿1为0怎么办?
A:这就是比较特殊的主元为0的情况,此时因为每一个方程地位都相等,所以只需将主元所在的行与下方主元位置非0的行互换即可。
追加Q:万一下面也没有呢?
A:那么方程就无解了,这种情况在后面也会提到。
于是就和

这个目标状态对应起来了。
然后就想摩拳擦掌的解了。
但是发现右边的b还没有代入矩阵。
于是
第二步:对增广矩阵消元
所谓增广矩阵?
增广矩阵(又称扩增矩阵)就是在系数矩阵的右边添上一列,这一列是线性方程组的等号右边的值。 -----百度百科
其实就是多出b那一列啦
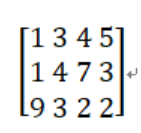
如上
增广矩阵的操作与左侧的系数矩阵完全一样,刚开始单列系数矩阵只是一个由简入难的过程,加深对高斯消元的理解。咸鱼限于篇幅原因,就不再赘述。
第三步:回带
最后经过一系列的消元,就得到了如下矩阵:

然后把矩阵再写回方程组:
{ x 1 + 3 x 2 + 4 x 3 = 5 0 x 1 + 1 x 2 + 3 x 3 = − 2 0 x 1 + 0 x 2 + 38 x 3 = − 91 \begin{cases}x_1+3x_2+4x_3=5\\0x_1+1x_2+3x_3=-2\\0x_1+0x_2+38x_3=-91\end{cases} ⎩⎪⎨⎪⎧x1+3x2+4x3=50x1+1x2+3x3=−20x1+0x2+38x3=−91
这样我们显而易见地就可以去掉系数为0的字母:
{ x 1 + 3 x 2 + 4 x 3 = 5 1 x 2 + 3 x 3 = − 2 38 x 3 = − 91 \begin{cases}x_1+3x_2+4x_3=5\\1x_2+3x_3=-2\\38x_3=-91\end{cases} ⎩⎪⎨⎪⎧x1+3x2+4x3=51x2+3x3=−238x3=−91
现在结果明了了,从下往上推:
依次可以得到
x 3 = − 91 38 = − 2.39 x_3=\frac{-91}{38}=-2.39 x3=38−91=−2.39
(保留了两位小数)
然后已知 x 3 x_3 x3,将其代入中间式子中的 x 3 x_3 x3,同理解得
x 2 = 5.18 x_2=5.18 x2=5.18
最后将 x 2 x_2 x2, x 3 x_3 x3都代回最上面的式子,得:
x 1 = − 0.97 x_1=-0.97 x1=−0.97
于是,对高斯消元的手动模拟就结束了QAQ
显然,这个在数学考试中会答不完题的,但是对于计算机来说,却是一个通用的方法。
时间复杂度: O ( n 3 ) O(n^3) O(n3)
虽然时间复杂度较高,不管怎样,我们已经找到了解决线性方程组的计算机通用方法,下面就用代码实现:
#include<cstdio>
#include<cmath>
#include<iostream>
using namespace std;
const double eps=1e-7 ;
double a[105][105],ans[105];
int main()
{int n;scanf("%d",&n);for(int i=1;i<=n;i++){ for(int j=1;j<=n+1;j++)//这里千万别忘了右侧那一列了 {scanf("%lf",&a[i][j]);}}for(int i=1;i<=n;i++){int m=i;for(int j=i+1;j<=n;j++)if(fabs(a[m][i])<fabs(a[j][i]))//fabs能取浮点数绝对值m=j;//找到当前这一列最大的数字,作为主元消元,这样能最大限度的避免精度误差 if(fabs(a[m][i])<eps)//这里要判精度,其实就是如果该位置的系数为0则无解(double没法准确处理这种精度 {printf("No Solution\n");return 0;}if(i!=m)swap(a[i],a[m]);//如果巧了,当前行不是最大行,那得罪了,你换下去吧,让未来的主元上来,好直接枚举之后的方程就行了 double d=a[i][i];for(int j=i;j<=n+1;j++)a[i][j]/=d;//将该位置的系数变为1 for(int j=i+1;j<=n;j++){d=a[j][i];for(int k=i;k<=n+1;k++){a[j][k]-=a[i][k]*d;//将其他的方程用两式相减的方法减去应当减掉的系数的值 }}}ans[n]=a[n][n+1];for(int i=n-1;i>=1;i--)//回带,最后一行直接写出答案,然后其他行还有等待前面处理出来,从后往前推即可 {ans[i]=a[i][n+1];//这里不难理解 for(int j=i+1;j<=n;j++){ans[i]-=a[i][j]*ans[j]; }}for(int i=1;i<=n;i++){ printf("%.2lf\n",ans[i]);}return 0;
}
这个模板可以在P3389 【模板】高斯消元法提交测试(话说貌似我之前已经放个一遍链接了
其他的地方应该都不难理解,就是为什么要让主元是最大的来避免误差?
这个是从期望上来证明的,有兴趣者阔以看看这一篇日报,应该就能想出来了吧。
大概就是:
设当前要消元的式子系数为 q i 1 , q i 2 , q i 3 . . . q i n q_{i1},q_{i2},q_{i3}...q_{in} qi1,qi2,qi3...qin
并假定我们主要针对的系数是 q i 1 q_{i1} qi1
则有
q j n = q j n − q j 1 q i 1 × q i w q_{jn}=q_{jn}-\frac{q_{j1}}{q_{i1}}\times q_{iw} qjn=qjn−qi1qj1×qiw
此时我们求的最大主元就是 q i 1 q_{i1} qi1,它越大,就说明 q j 1 q i 1 \frac{q_{j1}}{q_{i1}} qi1qj1的期望越小,这时较小的数给整个结果带来的影响也小,那么就不容易造成精度误差了QAQ
到此,高斯消元就结束了,但是
还有高斯消元的进阶版,能避免回带来求出答案。
2、高斯——约旦消元
说到避免回带来求出答案,大家应该能想到这种算法的目的,还是拿样例来说,就是把方程组变成:

这样,每个方程就能独立的解了。
那么,我们如何得到这种形式呢?
首先,我们依照朴素的高斯消元不难得到:

观察上下两个矩阵,不难得到,我们在消元时不仅仅消去主元所在式子下方的式子,而对于上方的式子也应当予以处理。
于是就开始了,下方是原图:
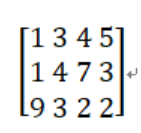
第一次与普通消元类似,即得:

但是第二次也要将第一行进行消元,得到:

然后就是最后一步(这一步是比朴素高斯消元要多的):

把矩阵写回方程组
{ x 1 + 0 x 2 + 0 x 3 = − 0.97 0 x 1 + x 2 + 0 x 3 = 5.18 0 x 1 + 0 x 2 + 38 x 3 = − 91 \begin{cases}x_1+0x_2+0x_3=-0.97\\0x_1+x_2+0x_3=5.18\\0x_1+0x_2+38x_3=-91\end{cases} ⎩⎪⎨⎪⎧x1+0x2+0x3=−0.970x1+x2+0x3=5.180x1+0x2+38x3=−91
系数为0去掉.jpg:
{ x 1 = − 0.97 x 2 = 5.18 38 x 3 = − 91 \begin{cases}x_1=-0.97\\x_2=5.18\\38x_3=-91\end{cases} ⎩⎪⎨⎪⎧x1=−0.97x2=5.1838x3=−91
这下子结果显然:
{ x 1 = − 0.97 x 2 = 5.18 x 3 = − 2.39 \begin{cases}x_1=-0.97\\x_2=5.18\\x_3=-2.39\end{cases} ⎩⎪⎨⎪⎧x1=−0.97x2=5.18x3=−2.39
下面是模板代码:
#include<cstdio>
#include<cmath>
#include<iostream>
using namespace std;
double a[105][105];
int main()
{int n;scanf("%d",&n);for(int i=1;i<=n;i++){for(int j=1;j<=n+1;j++){scanf("%lf",&a[i][j]);}}for(int i=1;i<=n;i++)//枚举列(项) {int m=i;for(int j=i+1;j<=n;j++)//选出该列最大系数 {if(fabs(a[j][i])>fabs(a[m][i]))//fabs是取浮点数的绝对值的函数{m=j;}}for(int j=1;j<=n+1;j++)//交换{swap(a[i][j],a[m][j]);}if(a[i][i]==0)//最大值等于0则说明该列都为0,肯定无解 {printf("No Solution\n");return 0;}for(int j=1;j<=n;j++)//每一项都减去一个数{if(j!=i)//不是主元那一项 {double d=a[j][i]/a[i][i];for(int k=i+1;k<=n+1;k++){a[j][k]-=a[i][k]*d;}}}}for(int i=1;i<=n;i++)//最后的结果系数可能不为1,所以记得消去常数 {printf("%.2lf\n",a[i][n+1]/a[i][i]);}return 0;
}
显然,这一份代码较上一份简练一些
3、例题
例题1:
P2455 [SDOI2006]线性方程组
题意简叙:
已知n元线性一次方程组,判断解的情况。
- 无实数解输出-1
- 无穷多实数解输出0
- 有唯一解,则输出解(小数点后保留两位小数)。具体格式见样例
分析:
这道题只是细化了前面模板题对无法得出唯一解情况的判断,于是顺便讲一下无解&&多解时的判断方法:
(我们知道,只要一个未知数无解或多解就可以说明整个方程的情况):
无解:

我们最直接的就是判断最后一行是否是
左边系数为0而右边系数不为0
但在容易疏漏情况,我们考虑到每一行,都会在其前面的消元中将唯一一个未知数留下来,也就都等同于第一行。
于是,每一行都可以按照最后一行的套路模板来判断:
i f ( a [ i ] [ i ] = = 0 if(a[i][i]==0 if(a[i][i]==0&& a [ i ] [ n + 1 ] ! = 0 ) a[i][n+1]!=0) a[i][n+1]!=0)无解
多解:

与上面对应的,我们很容易想到:
i f ( a [ i ] [ i ] = = 0 if(a[i][i]==0 if(a[i][i]==0&& a [ i ] [ n + 1 ] = = 0 ) a[i][n+1]==0) a[i][n+1]==0)多解
- 要注意先判断无解,如果是的话直接跳出,然后轮到多解。
因为多解首先建立在有解的基础上,如果哪一个未知数无解,整个方程自然不存在解,更不必说多解了。
然后其他的就和模板题完全一样了
例题2:
(这题我没有找到出处)
题目:【维他命的配方】
题意:
现有若干种维他命,问能否利用这些维他命配制出适合人需求的各种维生素
输入格式:
第一行:人需补充的维生素种类数 V ( 1 ≤ V ≤ 25 ) V(1\leq V\leq25) V(1≤V≤25)
第二行:V个数,第i个数为 V i V_i Vi,表示人体对第i种维生素的需求量 ( 1 ≤ V i ≤ 1000 ) (1\leq V_i\leq1000) (1≤Vi≤1000)
第三行:已知的维他命种类 G ( 1 ≤ G ≤ 15 ) G(1\leq G\leq15) G(1≤G≤15)
接下来是一个 G × V G\times V G×V的整数矩阵, A i j A_{ij} Aij表示第i种维他命中所含的第j中维生素的含量 ( 1 ≤ A i j ≤ 1000 ) (1\leq A_{ij}\leq1000) (1≤Aij≤1000)
输出格式:
第一行输出能否配制,能则“YES”,否则“NO”
第二行:若能配制则输出G个整数, G i G_i Gi表示第i中维他命所取的数列,多种方案输出任意一组。不能配制酒无需输出此行。
输入样例:
4
100 200 300 400
4
50 50 50 50
30 100 100 100
20 50 150 250
50 100 150 200
输出样例:
YES
1 1 1 0
分析:
首先要弄清维他命与维生素的区别。
然后就应该不难想到高斯消元。
设需要配制第i种维他命数量为 x i ( i ≤ 15 ) x_i(i\leq15) xi(i≤15)
根据题意可列出:
{ 50 x 1 + 30 x 2 + 20 x 3 + 50 x 4 = 100 50 x 1 + 100 x 2 + 50 x 3 + 100 x 4 = 200 50 x 1 + 100 x 2 + 150 x 3 + 150 x 4 = 300 50 x 1 + 100 x 2 + 250 x 3 + 200 x 4 = 400 \begin{cases}50x_1+30x_2+20x_3+50x_4=100\\50x_1+100x_2+50x_3+100x_4=200\\50x_1+100x_2+150x_3+150x_4=300\\50x_1+100x_2+250x_3+200x_4=400\end{cases} ⎩⎪⎪⎪⎨⎪⎪⎪⎧50x1+30x2+20x3+50x4=10050x1+100x2+50x3+100x4=20050x1+100x2+150x3+150x4=30050x1+100x2+250x3+200x4=400
- 这第一步很好想到,但是行列的顺序却容易弄错,仔细观察就会发现需要把 V i V_i Vi补到矩阵的第G+1行,然后每一列为一个方程计算。
列成矩阵的形式:

一通消元变成:
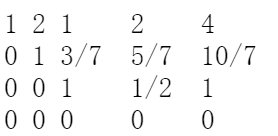
这时,我们惊奇的发现:最后一行都是0
(呀这怎么办!)

(刚才的知识怎么学的!不就是个多解情况吗?!)
水印打在人身上可还行
好了,多不多解不是关键,关键在于我们要怎么处理这一情况
但这是关键,也并不难。
我们只需懒一些将可能多解的未知数设为0,来尽可能的减少运算就行。
具体针对这个样例来说,就是设 x 4 = 0 x_4=0 x4=0,他的数量与答案无关,并不造成影响。
4、高斯消元注意事项:
模板不要背错- 为了避免精度问题,最好和eps比较而不是和0比较(虽然有时这个基本相同)
- 无解多解的判断情况以及顺序
- 遇到题目转换成高斯消元时不要兴奋的转换出错或弄反
5、后记
这一篇高斯消元的文章终于完工了,里面的矩阵配图和线性方程组的LaTeX书写不易,如果这篇文章对您有帮助,那请不吝赐赞。
这篇关于线性方程组QAQ的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!