basic MF矩阵分解

一 背景

对于推荐系统来说存在两大场景即评分预测（rating prediction）与Top-N推荐（item recommendation，item ranking）。评分预测场景主要用于评价网站，比如用户给自己看过的电影评多少分（MovieLens），或者用户给自己看过的书籍评价多少分（Douban）。其中矩阵分解技术主要应用于该场景。Top-N推荐场景主要用于购物网站或者一般拿不到显式评分信息的网站，即通过用户的隐式反馈信息来给用户推荐一个可能感兴趣的列表以供其参考。其中该场景为排序任务，因此需要排序模型来对其建模。因此，我们接下来更关心评分预测任务。

二 发展

 2.1 pure svd

当然提到矩阵分解，人们首先想到的是数学中经典的SVD（奇异值）分解，在这我命名为PureSVD（传统并经典着），直接上公式：当然SVD分解的形式为3个矩阵相乘，左右两个矩阵分别表示用户/项目隐含因子矩阵，中间矩阵为奇异值矩阵并且是对角矩阵，每个元素满足非负性，并且逐渐减小。因此我们可以只需要前  个因子来表示它。如果想运用SVD分解的话，有一个前提是要求矩阵是稠密的，即矩阵里的元素要非空，否则就不能运用SVD分解。很显然我们的任务还不能用SVD，所以一般的做法是先用均值或者其他统计学方法来填充矩阵，然后再运用SVD分解降维。

计算过程：

这里不讲证明，只讲计算流程：

2.2 basic mf

刚才提到的PureSVD首先需要填充矩阵，然后再进行分解降维，同时由于需要求逆操作（复杂度O(n^3)），存在计算复杂度高的问题，所以后来Simon Funk提出了FunkSVD的方法，它不在将矩阵分解为3个矩阵，而是分解为2个低秩的用户项目矩阵，同时降低了计算复杂度：

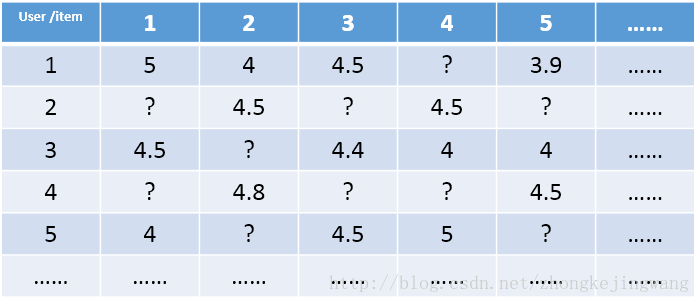这是一个极其稀疏的矩阵，这里把这个评分矩阵记为R，其中的元素表示user对item的打分，“？”表示未知的，也就是要你去预测的，现在问题来了：如何去预测未知的评分值呢？上一篇文章用SVD证明了对任意一个矩阵A，都有它的满秩分解：

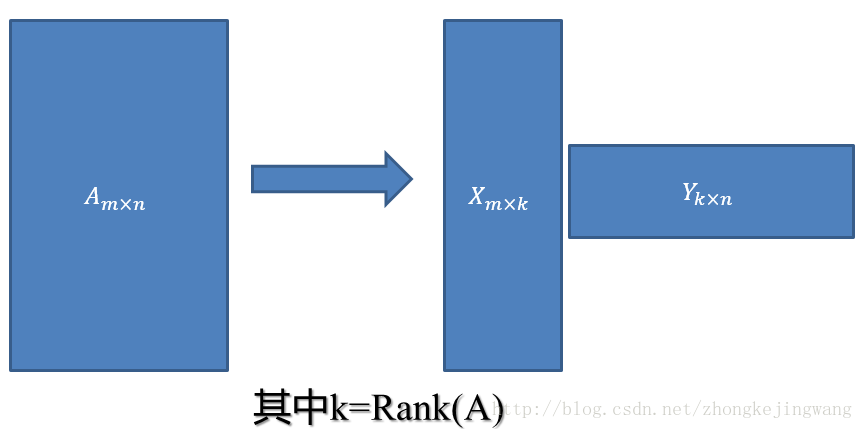那么刚刚的评分矩阵也存在这样一个分解，所以可以用两个矩阵P和Q的乘积来表示评分矩阵R：

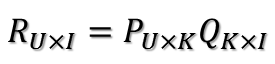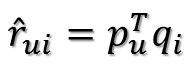上图中的U表示用户数，I表示商品数。然后就是利用R中的已知评分训练P和Q使得P和Q相乘的结果最好地拟合已知的评分，那么未知的评分也就可以用P的某一行乘上Q的某一列得到了。

未加正则化的损失函数：

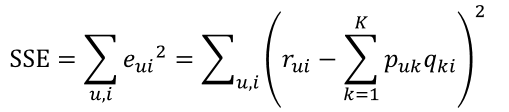它借鉴线性回归的思想，通过最小化观察数据的平方来寻求最优的用户和项目的隐含向量表示。同时为了避免过度拟合（Overfitting）观测数据，又提出了带有L2正则项的FunkSVD：加上正则化后的损失函数：

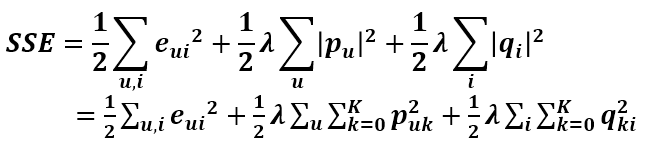三：梯度下降

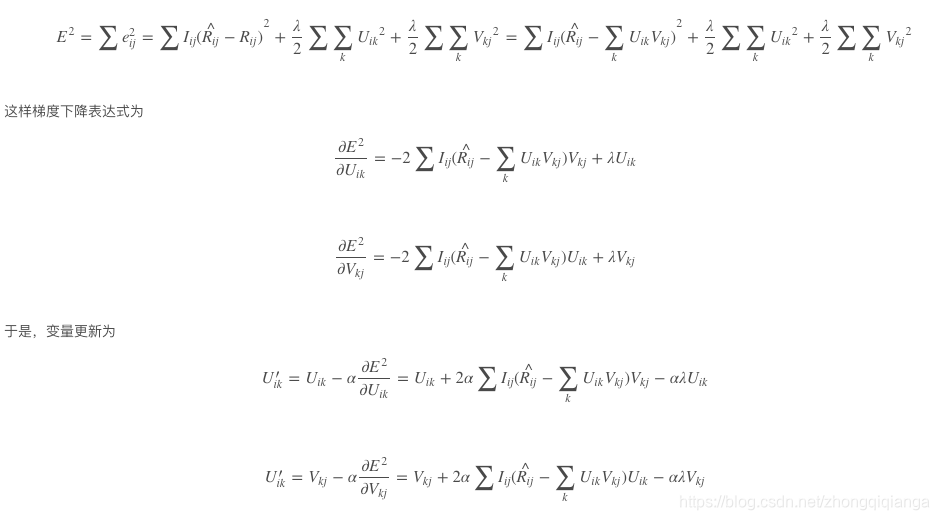四：代码实现

import numpy as np  
import matplotlib.pyplot as pltdef matrix(R, P, Q, K, alpha, beta):result=[]steps = 1while 1 :#使用梯度下降的一步步的更新P,Q矩阵直至得到最终收敛值steps = steps + 1    eR = np.dot(P,Q)e=0for i in range(len(R)):for j in range(len(R[i])):if R[i][j]>0:# .dot(P,Q) 表示矩阵内积,即Pik和Qkj k由1到k的和eij为真实值和预测值的之间的误差,eij=R[i][j]-np.dot(P[i,:],Q[:,j]) #求误差函数值，我们在下面更新p和q矩阵的时候我们使用的是化简得到的最简式，较为简便，#但下面我们仍久求误差函数值这里e求的是每次迭代的误差函数值，用于绘制误差函数变化图e=e+pow(R[i][j] - numpy.dot(P[i,:],Q[:,j]),2) for k in range(K):#在上面的误差函数中加入正则化项防止过拟合e=e+(beta/2)*(pow(P[i][k],2)+pow(Q[k][j],2))for k in range(K):#在更新p,q时我们使用化简得到了最简公式P[i][k]=P[i][k]+alpha*(2*eij*Q[k][j]-beta*P[i][k])Q[k][j]=Q[k][j]+alpha*(2*eij*P[i][k]-beta*Q[k][j])print('迭代轮次:', steps, '   e:', e)result.append(e)#将每一轮更新的损失函数值添加到数组result末尾#当损失函数小于一定值时，迭代结束if eij<0.00001:breakreturn P,Q,resultR=[[5,3,1,1,4],[4,0,0,1,4],[1,0,0,5,5],[1,3,0,5,0],[0,1,5,4,1],[1,2,3,5,4]]R=numpy.array(R)alpha = 0.0001 #学习率
beta = 0.002 #N = len(R)
M = len(R[0])
K = 2p = numpy.random.rand(N, K) #随机生成一个 N行 K列的矩阵
q = numpy.random.rand(K, M) #随机生成一个 M行 K列的矩阵P, Q, result=matrix(R, p, q, K,  alpha, beta)
print("矩阵Q为：\n",Q)
print("矩阵P为：\n",P)
print("矩阵R为：\n",R)
MF = numpy.dot(P,Q)
print("预测矩阵：\n",MF)#下面代码可以绘制损失函数的收敛曲线图
n=len(result)
x=range(n)
plt.plot(x, result,color='b',linewidth=3)
plt.xlabel("generation")
plt.ylabel("loss")
plt.show()

参考资料：

https://blog.csdn.net/qq_42057046/article/details/96454595