本文主要是介绍简单了解Knowledge distillation知识蒸馏,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
论文:Distilling the Knowledge in a Neural Network
一、什么是知识蒸馏,为什么要使用知识蒸馏?
知识蒸馏就是把一个大模型的知识迁移到小模型上,因为大模型虽然能达到较高的精度,但它的训练往往需要大量的资源和时间,小模型的训练需要的资源少,训练速度快,但它的精度往往不如大模型。显然,不是每个人都拥有足够的资源训练大模型,为了使用更少的资源、更快的速度,并且精度不能太差,不如让小模型Student学习大模型Teacher的知识,用更少的资源就能达到不错的精度。
二、知识是什么?
首先,区分硬标签和软标签,硬标签就是对分类结果,1就是1,0就是0,一只猫判断它是猫的概率是1,是狗的概率是0,软标签就是用概率给它一个不那么确定的标签,一只猫判断它是猫的概率是0.8,是狗的概率是0.2。
硬标签是我们数据集中通常已知的,一个模型经过训练后它输出的往往是软标签,软标签比硬标签具有更多的知识,比如图片猫的概率是0.8,狗的概率是0.2,说明猫和狗在一定程度上有相似性,而和苹果的相似性为0,这给了我们类别之间更多的关联和信息。
因此,小模型除了利用已知的硬标签,还可以从大模型给的预测软标签中学习更多的“知识”。
三、如何蒸馏知识
Student既要学习真实标签,也就是硬标签,还要学习Teacher给的软标签,那么损失函数就定义为:
L=CE(y,p)+αCE(q,p)
y是真实标签,p是Student的预测,q是Teacher的预测。
此外,由于Softmax通常把不同类的预测概率区分的很大,比如猫的是0.999,狗是0.001,苹果是0,这样狗和苹果和猫的相似度几乎都一样为0了,为了避免这种情况,加入温度Temperature,让每个类的预测差距不那么大:
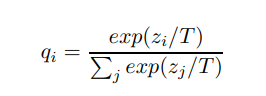
这样更有利于Student学习到知识。
四、具体应用
kl散度计算:
# 计算完kl散度总和再除以batch_size
F.kl_div(s_pre, t_pre, reduction='batchmean')
# 计算每个p(x_i)log(p(x_i)/q(x_i))
F.kl_div(s_pre, t_pre, reduction = 'none')
这篇关于简单了解Knowledge distillation知识蒸馏的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





