本文主要是介绍吴恩达老师机器学习ex5.Regularized Linear Regression and Bias v.s.Variance,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
吴恩达 机器学习 第六周作业 Regularized Linear Regression and Bias v.s.Variance
Octave代码
linearRegCostFunction.m
function [J, grad] = linearRegCostFunction(X, y, theta, lambda)
%LINEARREGCOSTFUNCTION Compute cost and gradient for regularized linear
%regression with multiple variables
% [J, grad] = LINEARREGCOSTFUNCTION(X, y, theta, lambda) computes the
% cost of using theta as the parameter for linear regression to fit the
% data points in X and y. Returns the cost in J and the gradient in grad% Initialize some useful values
m = length(y); % number of training examples% You need to return the following variables correctly
J = 0;
grad = zeros(size(theta));% ====================== YOUR CODE HERE ======================
% Instructions: Compute the cost and gradient of regularized linear
% regression for a particular choice of theta.
%
% You should set J to the cost and grad to the gradient.
%% fprintf('X:%d.\n', size(X));
% fprintf('theta:%d.\n', size(theta));
% fprintf('y:%d.\n', size(y));
J = 0.5 / m * sum((X * theta - y) .^ 2) + 0.5 / m * lambda * sum(theta(2 : end, :) .^ 2);% grad = 1 / m * sum((X * theta - y) .* X(:, 2 : end)) + lambda / m * theta(2 : end, :);
grad = 1 / m * X' * (X * theta - y) + lambda / m * theta;
grad(1) = 1 / m * sum(X * theta - y);% =========================================================================grad = grad(:);end
learningCurve.m
function [error_train, error_val] = ...learningCurve(X, y, Xval, yval, lambda)
%LEARNINGCURVE Generates the train and cross validation set errors needed
%to plot a learning curve
% [error_train, error_val] = ...
% LEARNINGCURVE(X, y, Xval, yval, lambda) returns the train and
% cross validation set errors for a learning curve. In particular,
% it returns two vectors of the same length - error_train and
% error_val. Then, error_train(i) contains the training error for
% i examples (and similarly for error_val(i)).
%
% In this function, you will compute the train and test errors for
% dataset sizes from 1 up to m. In practice, when working with larger
% datasets, you might want to do this in larger intervals.
%% Number of training examples
m = size(X, 1);% You need to return these values correctly
error_train = zeros(m, 1);
error_val = zeros(m, 1);% ====================== YOUR CODE HERE ======================
% Instructions: Fill in this function to return training errors in
% error_train and the cross validation errors in error_val.
% i.e., error_train(i) and
% error_val(i) should give you the errors
% obtained after training on i examples.
%
% Note: You should evaluate the training error on the first i training
% examples (i.e., X(1:i, :) and y(1:i)).
%
% For the cross-validation error, you should instead evaluate on
% the _entire_ cross validation set (Xval and yval).
%
% Note: If you are using your cost function (linearRegCostFunction)
% to compute the training and cross validation error, you should
% call the function with the lambda argument set to 0.
% Do note that you will still need to use lambda when running
% the training to obtain the theta parameters.
%
% Hint: You can loop over the examples with the following:
%
% for i = 1:m
% % Compute train/cross validation errors using training examples
% % X(1:i, :) and y(1:i), storing the result in
% % error_train(i) and error_val(i)
% ....
%
% end
%% ---------------------- Sample Solution ----------------------for i = 1:m;X_temp = X(1:i, :);
y_temp = y(1:i, :);
% Xval_temp = Xval(1:i, :);
% yval_temp = yval(1:i, :);
[theta] = trainLinearReg(X_temp, y_temp, lambda);
grad = zeros(size(theta));
[error_train(i), grad] = linearRegCostFunction(X_temp, y_temp, theta, 0);
[error_val(i), grad] = linearRegCostFunction(Xval, yval, theta, 0);end;% -------------------------------------------------------------% =========================================================================end
polyFeatures.m
function [X_poly] = polyFeatures(X, p)
%POLYFEATURES Maps X (1D vector) into the p-th power
% [X_poly] = POLYFEATURES(X, p) takes a data matrix X (size m x 1) and
% maps each example into its polynomial features where
% X_poly(i, :) = [X(i) X(i).^2 X(i).^3 ... X(i).^p];
%% You need to return the following variables correctly.
X_poly = zeros(numel(X), p);% ====================== YOUR CODE HERE ======================
% Instructions: Given a vector X, return a matrix X_poly where the p-th
% column of X contains the values of X to the p-th power.
%
% for i = 1:p;% X_poly(:, i) = X .^ i;if i == 1X_poly = X;elseX_poly = [X_poly X .^ i];end;
end;% =========================================================================end
validationCurve.m
function [lambda_vec, error_train, error_val] = ...validationCurve(X, y, Xval, yval)
%VALIDATIONCURVE Generate the train and validation errors needed to
%plot a validation curve that we can use to select lambda
% [lambda_vec, error_train, error_val] = ...
% VALIDATIONCURVE(X, y, Xval, yval) returns the train
% and validation errors (in error_train, error_val)
% for different values of lambda. You are given the training set (X,
% y) and validation set (Xval, yval).
%% Selected values of lambda (you should not change this)
lambda_vec = [0 0.001 0.003 0.01 0.03 0.1 0.3 1 3 10]';% You need to return these variables correctly.
error_train = zeros(length(lambda_vec), 1);
error_val = zeros(length(lambda_vec), 1);% ====================== YOUR CODE HERE ======================
% Instructions: Fill in this function to return training errors in
% error_train and the validation errors in error_val. The
% vector lambda_vec contains the different lambda parameters
% to use for each calculation of the errors, i.e,
% error_train(i), and error_val(i) should give
% you the errors obtained after training with
% lambda = lambda_vec(i)
%
% Note: You can loop over lambda_vec with the following:
%
% for i = 1:length(lambda_vec)
% lambda = lambda_vec(i);
% % Compute train / val errors when training linear
% % regression with regularization parameter lambda
% % You should store the result in error_train(i)
% % and error_val(i)
% ....
%
% end
%
%for i = 1:length(lambda_vec);[theta] = trainLinearReg(X, y, lambda_vec(i));
grad = zeros(size(theta));
[error_train(i), grad] = linearRegCostFunction(X, y, theta, 0);
[error_val(i), grad] = linearRegCostFunction(Xval, yval, theta, 0);end;% =========================================================================end
运行结果
Octave command prompt
octave:35> ex5Loading and Visualizing Data ...
Program paused. Press enter to continue.Cost at theta = [1 ; 1]: 303.993192
(this value should be about 303.993192)
Program paused. Press enter to continue.……lambda Train Error Validation Error0.000000 0.183694 21.9074770.001000 0.170768 19.7177500.003000 0.180128 17.8908670.010000 0.222678 17.0924930.030000 0.281851 12.8316820.100000 0.459318 7.5870120.300000 0.921760 4.6368331.000000 2.076188 4.2606253.000000 4.901351 3.82290710.000000 16.092213 9.945508
Program paused. Press enter to continue.
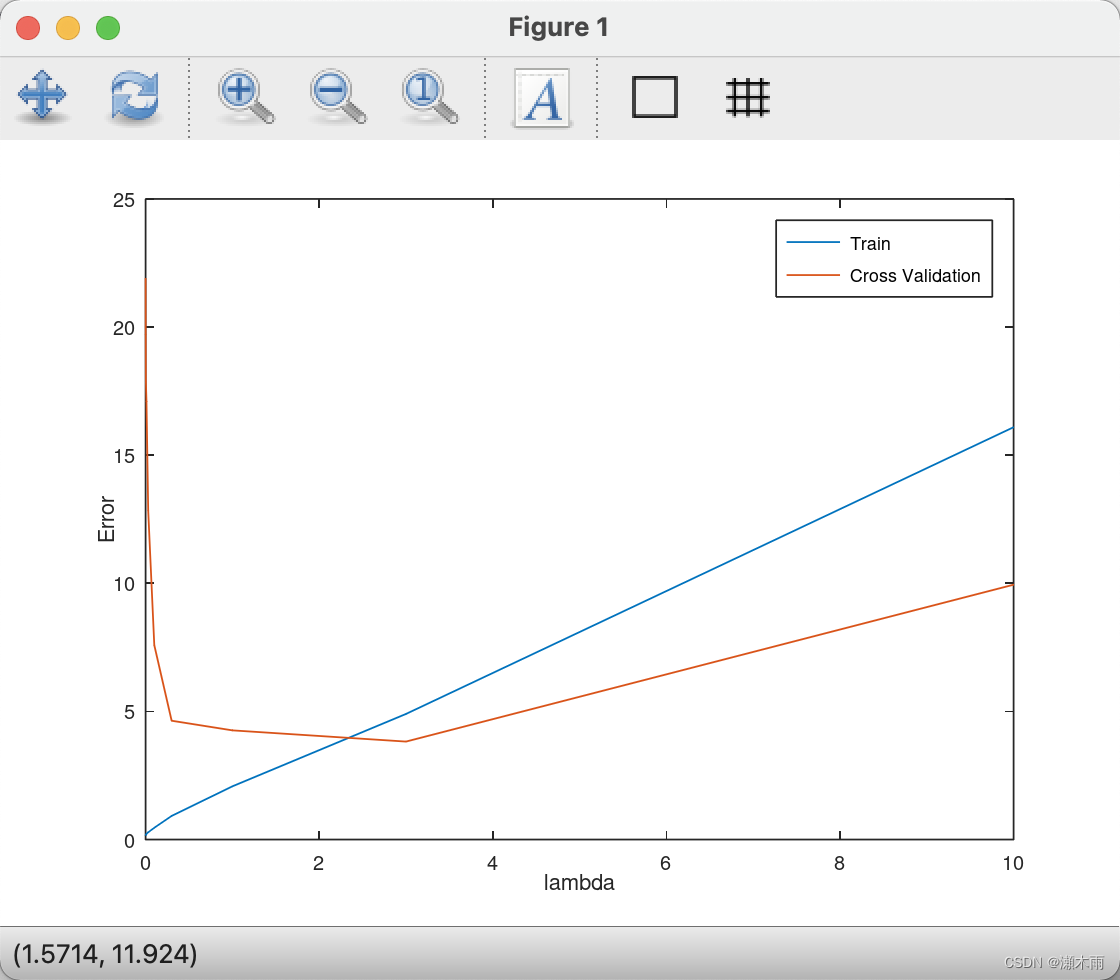
这篇关于吴恩达老师机器学习ex5.Regularized Linear Regression and Bias v.s.Variance的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







