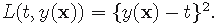variance专题

方差（Variance） 偏差（bias） 过拟合 欠拟合

方差（Variance） 偏差（bias） 过拟合 欠拟合

机器学习中方差（Variance）和偏差（bias）的区别？与过拟合欠拟合的关系？   (1)bias描述的是根据样本拟合出的模型的输出预测结果的期望与样本真实结果的差距，简单讲，就是在样本上拟合的好不好。 低偏差和高方差（对应右上图）是使得模型复杂，增加了模型的参数，这样容易过拟合。 这种情况下，形象的讲，瞄的很准，但手不一定稳。 （2）varience描述的是样本上训练出来的模型
阅读更多...
High-variance latent spaces

High-variance latent spaces

“High-variance latent spaces” 这个术语通常出现在机器学习和人工智能领域，特别是在涉及到生成模型、表示学习和特征学习的时候。在这个上下文中，“latent space” 指的是一个多维空间，其中每个点代表输入数据的一个潜在表示或特征向量。这个空间是“潜在”的，因为它不是直接观察到的数据，而是通过某种学习算法从原始数据中提取出来的。 “High-variance” 描述
阅读更多...
PyTorch 入坑十：模型泛化误差与偏差(Bias)、方差(Variance)

PyTorch 入坑十：模型泛化误差与偏差(Bias)、方差(Variance)

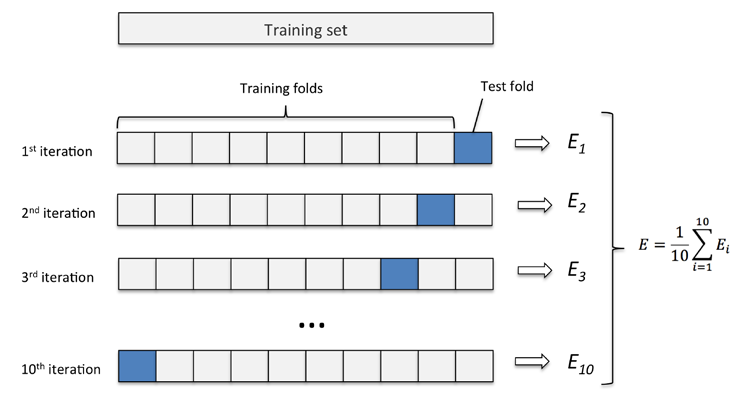
问题 阅读正文之前尝试回答以下问题，如果能准确回答，这篇文章不适合你；如果不是，可参考下文。 为什么会有偏差和方差？偏差、方差、噪声是什么？泛化误差、偏差和方差的关系？用图形解释偏差和方差。偏差、方差窘境。偏差、方差与过拟合、欠拟合的关系？偏差、方差与模型复杂度的关系？偏差、方差与bagging、boosting的关系？偏差、方差和K折交叉验证的关系？如何解决偏差、方差问题？ 本文主要参考知
阅读更多...
sns报错 UserWarning: Dataset has 0 variance； skipping density estimate.

sns报错 UserWarning: Dataset has 0 variance； skipping density estimate.

报错信息 UserWarning: Dataset has 0 variance; skipping density estimate. Pass warn_singular=False to disable this warning. 三维数组维度(1000, 27,1)，取出第一个元素画出分布图保存检查错误原因，print(Mcases[:,:,0].shape) 显示维度(1000, 27)
阅读更多...
Andrew Ng机器学习week6(Regularized Linear Regression and Bias/Variance)编程习题

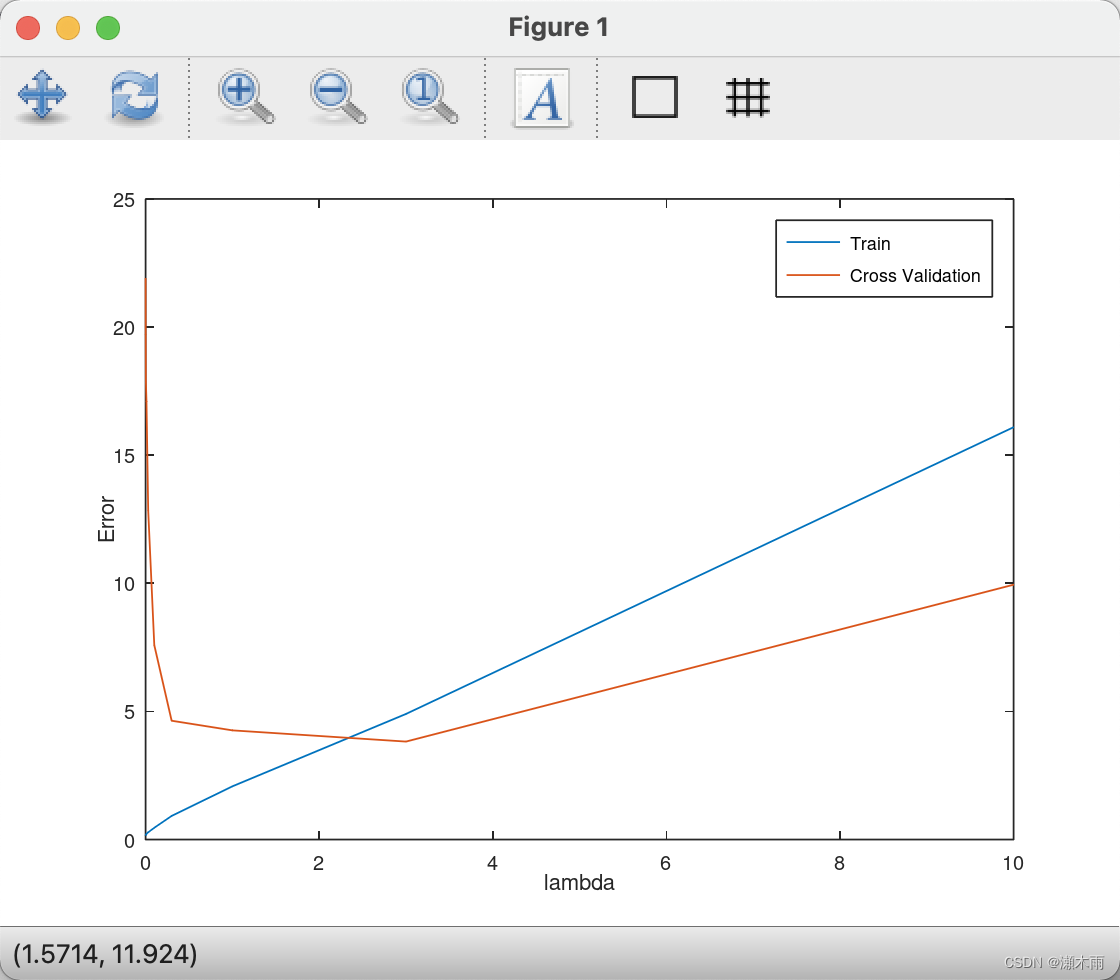
Andrew Ng机器学习week6(Regularized Linear Regression and Bias/Variance)编程习题

Andrew Ng机器学习week6(Regularized Linear Regression and Bias/Variance)编程习题 linearRegCostFunction.m function [J, grad] = linearRegCostFunction(X, y, theta, lambda)%LINEARREGCOSTFUNCTION Compute cost an
阅读更多...
【概率论】4-3:方差(Variance)

【概率论】4-3:方差(Variance)

原文地址1：https://www.face2ai.com/Math-Probability-4-3-Variance转载请标明出处 Abstract: 本文介绍继期望之后分布的另一个重要数学性质，方差 Keywords: Variance,Standard Deviation 方差 这两天更新有点频繁，但是没办法，必须快速的完成的基础知识积累，毕竟时间是有限的，还要留出更多的时间用于更进一步
阅读更多...
bias和variance

bias和variance

在A Few Useful Thingsto Know about Machine Learning中提到，可以将泛化误差（gener-alization error）分解成bias和variance理解。   Bias: a learner’s tendency to consistently learn the same wrong thing，即度量了某种学习算法的平均估计结果所能逼
阅读更多...
理解Mean-Variance Portfolio Theory In MPT

理解Mean-Variance Portfolio Theory In MPT

Markowitz Mean-Variance Portfolio Theory An investment instrument that can be bought and sold is often called an asset. Suppose we purchase an asset for x 0 x_0 x0​ dollars on one date and then late
阅读更多...
(done) 机器学习中的方差 variance 和 偏差 bias 怎么理解？

(done) 机器学习中的方差 variance 和 偏差 bias 怎么理解？

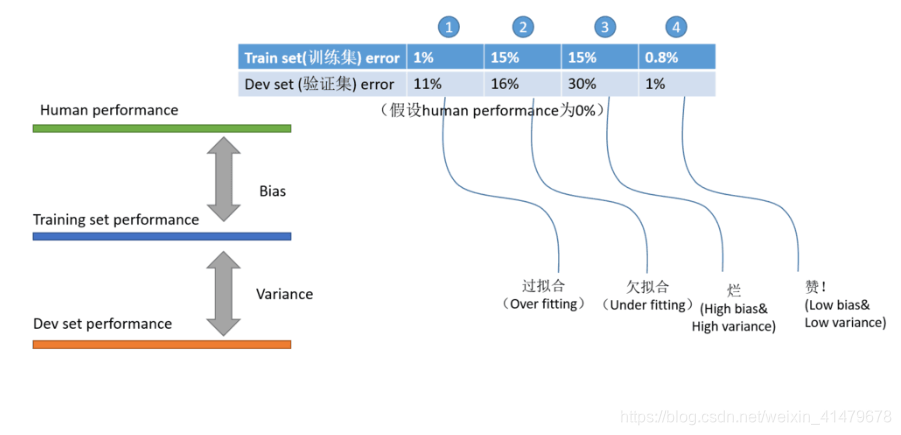
来源：https://blog.csdn.net/weixin_41479678/article/details/116230631 情况1属于：低 bias，高 variance (和 human performance 相近，但和 验证集dev set 相远) 通常意味着模型训练轮数太多 情况2属于：高 bias，低 variance (和 human performance 相远，
阅读更多...
偏差Bias和方差Variance的区别 不要只会画靶子图 P值

偏差Bias和方差Variance的区别 不要只会画靶子图 P值

偏差 Bias 偏差指的是由所有采样得到的大小为m的训练数据集训练出的所有模型的输出的平均值和真实模型输出之间的偏差。 方差 Variance 方差指的是由所有采样得到的大小为m的训练数据集训练出的所有模型的输出的方差。方差通常是由于模型的复杂度相对于训练样本数m过高导致的，比如一共有100个训练样本，而我们假设模型是阶数不大于200的多项式函数。由方差带来的误差通常体现在测试误差相对于训练
阅读更多...
偏差-方差分解bias-variance decomposition

偏差-方差分解bias-variance decomposition

方差、偏差的直观意义 方差维基百科定义： Var ⁡ ( X ) = E [ ( X − μ ) 2 ] 其 中 μ = E ( X ) \operatorname{Var}(X)=\mathrm{E}\left[(X-\mu)^{2}\right] 其中\mu=\mathrm{E}(X) Var(X)=E[(X−μ)2]其中μ=E(X) 在给定数据集中 方差： var ⁡ ( x ) =
阅读更多...
方差分解（variance decomposition）研究发展史

方差分解（variance decomposition）研究发展史

方差分解（variance decomposition）研究发展史 1 早期技术概述1.1 方差组分分析（variance components analysis, VCA ）1.2 方差分析（Analysis of Variance，简称ANOVA） 2 交叉嵌套数据结构和早期方差分解技术的局限性3 多层次建模方法的方差分解参考 1 早期技术概述 方差分解如下： 下面介绍方差
阅读更多...
机器学习基础题——什么是Bias?什么是Variance?如何解决过拟合和欠拟合问题？

机器学习基础题——什么是Bias?什么是Variance?如何解决过拟合和欠拟合问题？

机器学习基础 1.什么是Bias?什么是Variance?2.如何解决过拟合和欠拟合问题？ Bias：反映的是模型在样本上的输出与真实值之间的误差，即模型的精准度（单个模型的学习能力） Variance：反映的是模型每一次输出结果与模型输出期望之间的误差，即模型的稳定性（同一个算法在不同的数据集上的不稳定性） 机器学习中的调优方向：High Bias + Low Variance,即上图左
阅读更多...
机器学习中的Bias(偏差)，Error(误差)，和Variance(方差)有什么区别和联系？

机器学习中的Bias(偏差)，Error(误差)，和Variance(方差)有什么区别和联系？

原文：http://www.zhihu.com/question/20448464 5 个回答 Jason Gu， 肖子达、RainVision、舟舟舟 等人赞同 偏差：描述的是预测值（估计值）的期望与真实值之间的差距。偏差越大，越偏离真实数据，如下图第二行所示。 方差：描述的是预测值的变化范围，离散程度，也就是离其期望值的距离。方差越大，数据的分布越分散，如下
阅读更多...
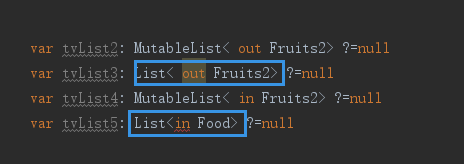
projection is conflicting with variance of the corresponding type parameter of list

projection is conflicting with variance of the corresponding type parameter of list

第二行和第四行分别警告和报错。 解析 List不可修改，MutableList是可以修改的。out是输出，对应Java ? extends ,限制了上限，导致的结果是只能取值get；相应的 in 输出，对应Java的 ？super ，限制了下界，只能add，所以不可改变是没有意义的，导致报错
阅读更多...
吴恩达老师机器学习ex5.Regularized Linear Regression and Bias v.s.Variance

吴恩达老师机器学习ex5.Regularized Linear Regression and Bias v.s.Variance

吴恩达 机器学习 第六周作业 Regularized Linear Regression and Bias v.s.Variance Octave代码 linearRegCostFunction.m function [J, grad] = linearRegCostFunction(X, y, theta, lambda)%LINEARREGCOSTFUNCTION Compute co
阅读更多...
Bias-Variance Tradeoff (权衡偏差与方差)

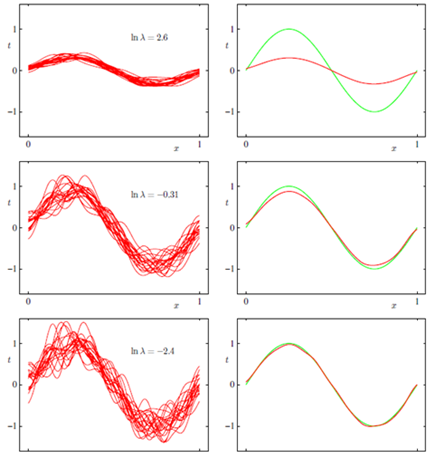
Bias-Variance Tradeoff (权衡偏差与方差)

转自：https://blog.csdn.net/qq_30490125/article/details/52401773 对学习算法除了通过实验估计其泛化性能，我们还希望了解“为什么”具有这样的性能。“偏差－方差分解”（bias-variance decomposition）是解释学习算法泛化性能的一种重要工具。 偏差和方差 理解偏差和方差这两个不同来源导致的误差可以帮助我们更好得拟合数据
阅读更多...
Bias与Variance的理解

Bias与Variance的理解

一、概念介绍     Error=(Bias)^2 + Variance+Noise Error（误差）：整个模型的准确度，即模型预测结果与实际结果之间的差距。 Bias(偏差):度量了估计期望（模型对数据集预测结果的平均值与实际值之间的差距） Variance(方差)：反映的是模型每一次输出结果与模型输出期望之间的误差，即模型的稳定性。（模型预测的结果与与模型对样本集预测的平均值之间的差
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2