LeetCode高频题：n杯溶液按照顺序排成一排，可以混合相邻2杯，合并代价/时间是两杯质量和，经过n-1次合并为1杯，最小时间/代价是多少

LeetCode高频题：n杯溶液按照顺序排成一排，可以混合相邻2杯，合并代价/时间是两杯质量和，经过n-1次合并为1杯，最小时间/代价是多少？

提示：本题是系列LeetCode的150道高频题，你未来遇到的互联网大厂的笔试和面试考题，基本都是从这上面改编而来的题目
互联网大厂们在公司养了一大批ACM竞赛的大佬们，吃完饭就是设计考题，然后去考应聘人员，你要做的就是学基础树结构与算法，然后打通任督二脉，以应对波云诡谲的大厂笔试面试题！
你要是不扎实学习数据结构与算法，好好动手手撕代码，锻炼解题能力，你可能会在笔试面试过程中，连题目都看不懂！比如华为，字节啥的，足够让你读不懂题

文章目录

• LeetCode高频题：n杯溶液按照顺序排成一排，可以混合相邻2杯，合并代价/时间是两杯质量和，经过n-1次合并为1杯，最小时间/代价是多少？
• • @[TOC](文章目录)
• 题目
• 一、审题
• 遇到笔试时间不够的话，你就暴力干完事了
• 本题的正确解题姿势：把相邻的k个元素合并为1个数，代价是k个数字的和
• f(arr,L,R,part,k,sum)内部怎么合并？
• 总结

题目

有n杯溶液按照顺序排成一排，编号为1，2，3，，，n，n<=100，每一杯有质量，现在将n杯溶液混合，只有相邻的两杯可以融合，混合之后质量叠加不变，代价是两杯质量的和，经过n-1次混合，所有溶液混在一起，请求出混合他们的最少代价。

输入描述：
输入有n+1行
第一行一个整数n，表示n杯溶液
第2–n+1行，每行一个整数，表示每一杯溶液的质量

输出描述：
就一个整数，表示混合所有融合所需的总时间最少时间。

一、审题

示例：
3
5
3
4
输出：
19
3+4代价7
5+7代价12
拢共代价就是19

遇到笔试时间不够的话，你就暴力干完事了

咋搞呢？？

可不就是相邻俩求和，看看谁小，先合并谁呗

然后要把数组缩进一下，将没有合并的那部分整体往左挪
比如下面arr
显然1+0最小
把和1放入3位置，然后将5–N-1所有元素往左挪一个位置

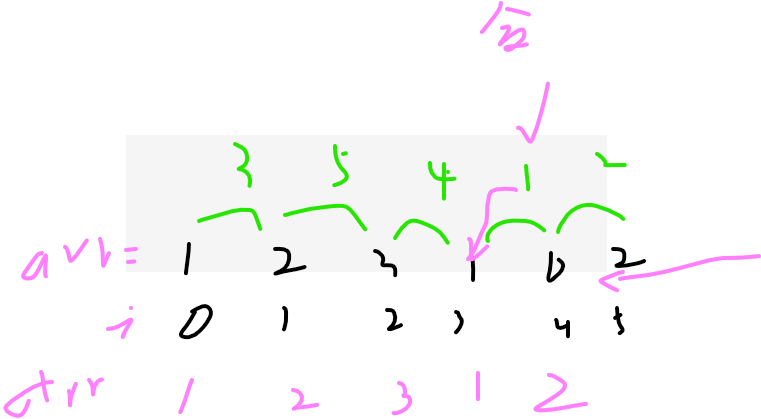
首先，你相邻求和，就需要整体o（n）复杂度
然后你还要将右边部门挪到左边，又是o（n）
帧挺复杂度的，暴力可以搞，但是时间太慢了
笔试估计就ac一部分

这个题，精巧的解法，就是动态规划

不要怕难，学过的题目一定会在你秋招笔试中用到的，当年华为的机试，我就遇到一个原题，非常刺激，而且是华为第3题
原题就意味着通过速度很快，非常棒，而且华为的笔试三题得分比例是100:200:300
100分及格
如果第三题遇到了原题，岂不是炸了！！！
刺激

本题的正确解题姿势：把相邻的k个元素合并为1个数，代价是k个数字的和

不就是本题k=2的情况吗？

相邻的k=2个元素合并，合并代价/时间就是两者和和，溶液不溶液的没啥关系

下次换一个题目，换牛奶了，换水桶了，没啥区别，就是原题

所以，这里我们就讨论k，将来题目换成相邻3杯溶液混合，不也是本题的原题吗？？？
对不

OK

这题我就说过了真的【之前我就讲过，因为这题很有趣的】
【1】数组arr相邻的k个合并为1个数字，最终将arr合并为1个数字的最小代价是？

相邻k个数合并的话，代价就是累加和

因此算L–R上的合并代价必然是sum[R+1]-sum[L]，如果左闭右开的话

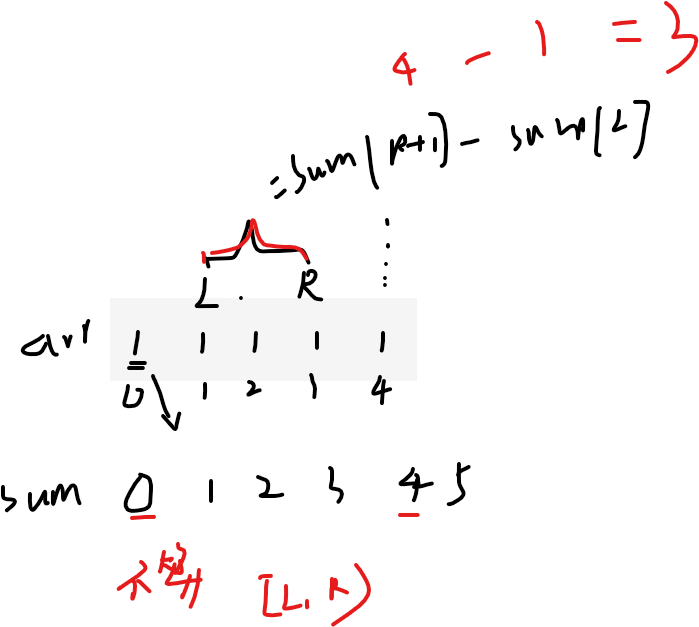
啥意思呢？就是sum是[L–R)上的累加和，sum[0]就是不包含arr0时的累加和自然是0
所以上面的arr的sum[0]就是0
sum[1]不包含1位置，就是arr0=1
sum[2]不包含2位置，就是arr0+arr1=2
sum[3]不包含3位置，就是arr0+arr1+arr3=3
sum[4]不包含4位置，就是arr0+arr1+arr3+arr4=4
sum[5]不包含5位置，就是arr0+arr1+arr3+arr4+arr5=5=sum[4]+arr[4]
懂？

因此有了sum前缀累加和
我们就可以随意捞L–R上的累加和了，左闭右开记住了，不包含R的

具体我们怎么合并呢？？？

我们想合并arr的L–R范围，让它最终变为1个数，而且合并代价最小

故，有arr的情况下，有前缀累加和sum，k已知的
将arr的L–R合并为part个数，返回这样合并的最小代价
这个函数定义为f(arr,L,R,part,k,sum)

主函数当然就是这样的，f(arr,0,N-1,part=1,k=2,sum)
啥意思呢？
有arr的情况下，有前缀累加和sum，k=2已知的，代表相邻俩溶液合并
将arr的0–N-1合并为part=1个数，返回这样合并的最小代价

就是本题要问你的意思

f(arr,L,R,part,k,sum)内部怎么合并？

其实很容易：
不就是卡条件吗

（1）如果L=R了，显然已经完成了任务，，如果part要求是1的话，不用合并了，代价就是0呗，part要不是1的话，没法搞啊，返回-1代价
（2）L<R的话，那我们要想办法把L–R上合并为part个？
如果part是1，必然先考虑把L–R上的数合并为k个，这里k=2，就是先把L–R上的合并为2个
最后一下子，将这俩合并为part=1个呗，这不就是题目要求的意思，这是最后一趟合并了
所以先调用f(arr,L,R,part= k ,k,sum)
得到代价为cost1
如果cost1不是-1，有效，现在的L–R就是k个了
比如下面L–R是3个，咱先合并一把，将L–R缩为2个

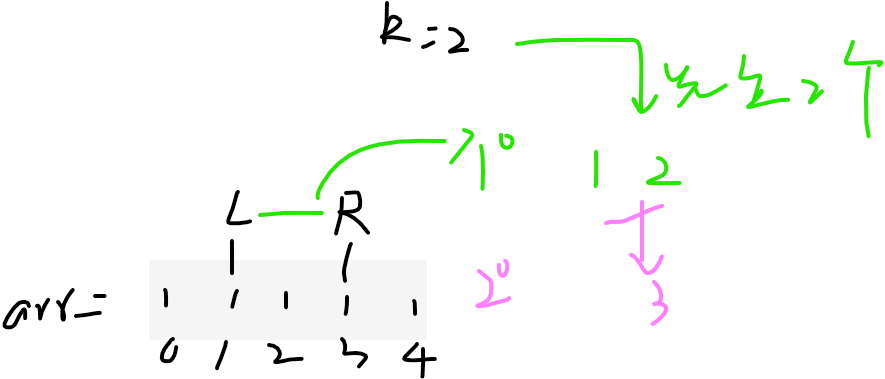
此时，L–R上就是2个了【这个是递归过程中你会发现的】
直接把这k个一起喝成合并了，代价就是sum[R+1]-sum[L]
你想想是不是？

（3）如果part不是1，那就要枚举合并的个数了
可以这样，你可以把L–R分为2部分，中间用mid来隔开
mid从L–R-1去枚举
啥意思？
我们可以先合并L–mid为1份，再合并mid+1–R为part-1【拢共咱不是要part份吗？】，
左右俩代价的和，的最小值，就是我们要的情况
所以就得枚举
比如下面L–R，你完全可以让左边1单独合并为1份，同时让后面四个先合并为part-1份，这样合起来就是L–R合并为part份，懂？

你也可以让左边2个合并为1分，剩下的合并为part-1分
以此类推

这里的话，其实我们必须合并相邻的k个
所以下一次mid在枚举时，直接让mid+k-1就行

这样一次性搞k个才能合并为1分的。

其实也就这么些情况了
手撕代码你就知道了

    //复习，题目可以改编为搞溶液混合的题目，相邻2个混合，k=2//有arr的情况下，有前缀累加和sum，k已知的//将arr的L--R合并为part个数，返回这样合并的最小代价//这个函数定义为**f(arr,L,R,part,k,sum)**public static int g(int[] arr, int L, int R, int part, int k, int[] sum){//（1）如果L=R了，显然已经完成了任务，，如果part要求是1的话，不用合并了，代价就是0呗，part要不是1的话，没法搞啊，返回-1代价if (L == R) return part == 1 ? 0 : -1;//不是1个的话，不合适//（2）L<R的话，那我们要想办法把L--R上合并为part个？//如果part是1，必然先考虑把L--R上的数合并为k个，这里k=2，就是先把L--R上的合并为2个//最后一下子，将这俩合并为part=1个呗if (part == 1){int cost1 = g(arr, L, R, k, k, sum);return cost1 == -1 ? -1 : cost1 + sum[R + 1] - sum[L];//最后把L--R整体合并为1个}//（3）如果**part**不是1，那就要枚举合并的个数了//可以这样，你可以把L--R分为2部分，中间用mid来隔开//mid从L--R-1去枚举int cost = Integer.MAX_VALUE;for (int mid = L; mid < R; mid+=k - 1) {//一次只能融合k的倍数个//L--k-1就是k个int costL = g(arr, L, mid, 1, k, sum);int costR = g(arr, mid + 1, R, part - 1, k, sum);if (costL != -1 && costR != -1) cost = Math.min(cost, costL + costR);}//各个情况的最小值return cost;}

主函数：

    public static int minCostPartReview(int[]arr, int k){if (arr == null || arr.length == 0) return 0;int N = arr.length;int[] sum = new int[N + 1];//前缀累加和for (int i = 0; i < N; i++) {sum[i + 1] = sum[i] + arr[i];//从1开始真的加}return g(arr, 0, N - 1, 1, k, sum);}

上面说过的，从arr整个范围，将其合并为1个容器，最小代价是

测试：

    public static void test(){int[] arr = {5, 3, 4};int k = 2;//俩俩合并，谁先都是2,2，cost=4，然后合并2,2为4，成本为cost+=4=8//或者你左边1,1，为2，成本为2，然后变2,1,1，然和2,1位3，成本为3，累加成本为2+3==5//然后3与1合并为4，成本为4，累加成本为5+4==9，所以最节约的话是8System.out.println(minCostPart(arr, k));System.out.println(minCostPartDP(arr, k));System.out.println(minCostPartReview(arr, k));}public static void main(String[] args) {test();}

结果

19
19
19

至于如何该dp，记忆化搜索，请看我之前写得文章，今天就不重复了
笔试这样至少ac 75%
如果优化为记忆化搜索，100%通过肯定OK

总结

提示：重要经验：

1）将相邻的k个元素合并，代价是他们的累加和，这种题目就拿本题改编代码就行
3）笔试求AC，可以不考虑空间复杂度，但是面试既要考虑时间复杂度最优，也要考虑空间复杂度最优。