计算机图形学（九）：三维对象的表示（三维几何模型的CSG树和B-rep表示）

目录

构造表示法

体素构造CSG的原理和方法

空间形体的正则集合运算

建立实体模型的一般过程

空间形体的CSG树表示

边界表示法

计算机中表示三维形体的模型，按照几何特点进行分类，大体上可以分为三种：线框模型、表面模型和实体模型。如果按照表示物体的方法进行分类，实体模型基本上可以分为分解表示、构造表示CSG（Constructive Solid Geometry）和边界表示BREP（Boundary Representation）三大类。

构造表示法

CSG建模法，一个物体被表示为一系列简单的基本物体（如立方体、圆柱体、圆锥体等）的布尔操作的结果，数据结构为树状结构。树叶为基本体素或变换矩阵，结点为运算，最上面的结点对应着被建模的物体；而BREP的一个物体被表示为许多曲面（例如面片，三角形，样条）粘合起来形成封闭的空间区域。

更严谨的表述：

边界表示法是用实体的表面来表示实体的形状，它的基本元素是面、边、顶点。它以欧拉公式作为理论基础，要求实体的基本拓扑结构符合欧拉公式。目前采用的比较多的数据结构是翼边数据结构和半边数据结构（又称对称数据结构）。

实体构造表示法的基本思想是将简单的实体（又称体素）通过集合运算组成所需要的物体。其中，集合运算的实现过程由一棵二叉树来描述，二叉树的叶子节点表示体素或者几何变换的参数，非终端节点表示施加于其子结点的正则集合算子或几何变换的定义。

体素构造CSG的原理和方法

CSG(Constructive Solid Geometry)体素构造表示法，是用计算机进行实体造型的一种构形方法，也是一种新的构形思维方式。这种构形方法的描述，既符合空间形体的构形过程，又能满足计算机实体造型的要求。体素构造表示法把复杂的实体，看成由若干较简单的最基本实体经过一些有序的布尔运算而构造出来，这些简单的最基本的实体称为体素。

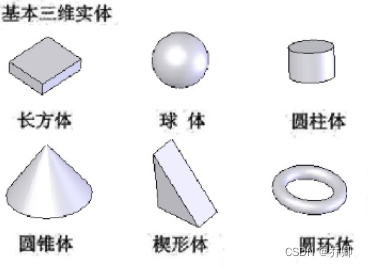
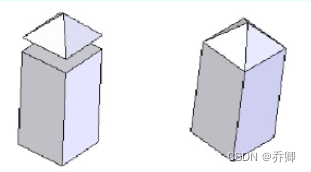
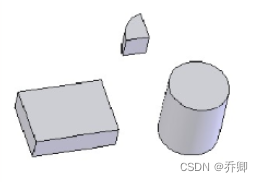
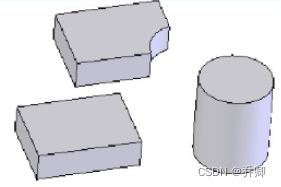
空间形体的正则集合运算

并：

交：

差：

建立实体模型的一般过程

从上到下，逐渐建立实体模型：

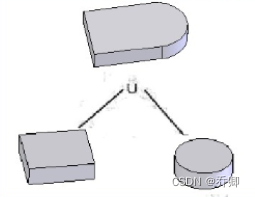
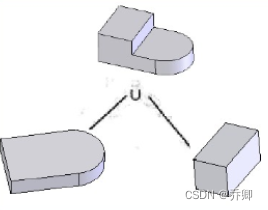
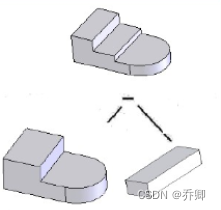
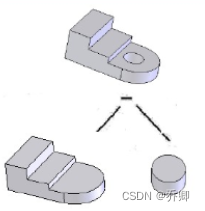
空间形体的CSG树表示

CSG树结构建立实体模型时使用的布尔运算，可以形成一个记录每步执行信息的层结构或者树结构。

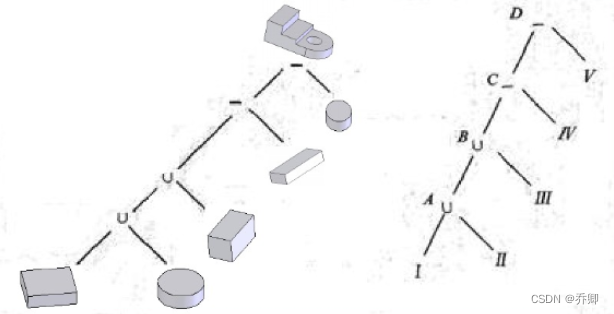
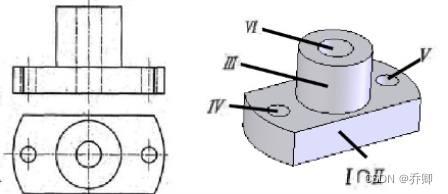
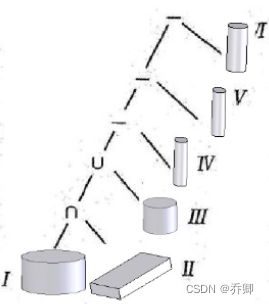
根据支架的投影，构造其CSG树：

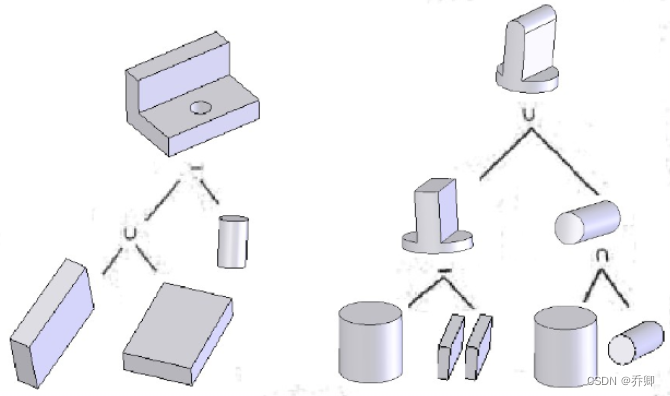
CSG总结

数据结构：二叉树结构，记录了实体所有基本体素的组成、正则集合运算和相关的几何变换。

特点：方法简洁，生成速度快，处理方便，无冗余信息，而且能够详细地记录构成实体的原始特征参数，甚至在必要时可修改体素参数或附加体素进行重新拼合。数据结构比较简单，数据量较小，修改比较容易，而且可以方便地转换成边界（Brep）表示。

缺点：没有详细几何信息，必须转化为其它形式才能对点、边、面等信息进行查询和编辑。由于信息简单，这种数据结构无法存贮物体最终的详细信息，例如边界、顶点的信息等。由于CSG表示受体素的种类和对体素操作的种类的限制，使得它表示形体的覆盖域有较大的局限性，而且对形体的局部操作（例如，倒角等等）不易实现，显示CSG表示的结果形体时需要的间也比较长。

边界表示法

B-rep的概念

通过面、环、边、顶点的几何和拓扑参数来表示实体。

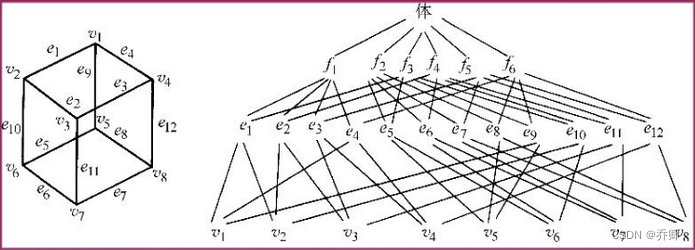
B-rep的总结

数据结构：是以边为中心的翼边结构，通过任意一条边，可以遍历整个实体所有几何元素。

BRep优点：
     1. 有较多的关于面、边、点及其相互关系的信息。
　 2. 有利于生成和绘制线框图、投影图，有利于计算几何特性，易于同二维绘图软件衔接和同曲面建模软件相关联。

BRep局限：
  由于它的核心信息是面，因而对几何物体的整体描述能力相对较差，无法提供关于实体生成过程的信息，也无法记录组成几何体的基本体素的元素的原始数据，同时描述物体所需信息量较多，边界表达法的表达形式不唯一。