Pseudo-Label : The Simple and Efficient Semi-Supervised Learning Method for Deep Neural Networks学习笔记

论文地址:Pseduo-Label
从DAFomer溯源到的论文

伪标签的介绍

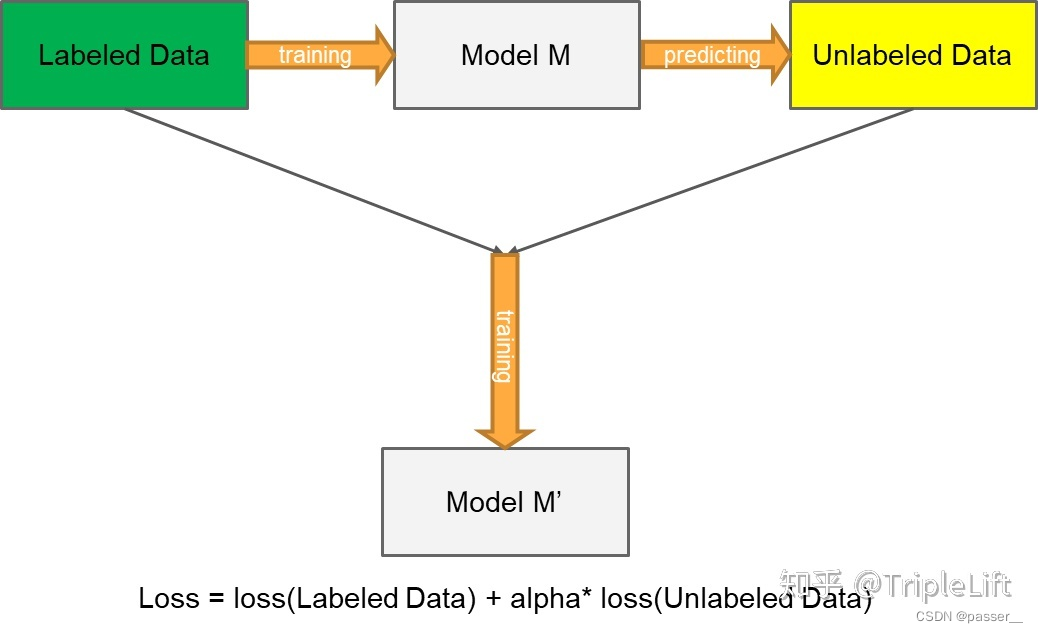
伪标签的介绍可以参考:伪标签（Pseudo-Labelling）——锋利的匕首，详细介绍了什么是伪标签方法以及伪标签方法的分类，本论文用到的方法就是上文中的 创新版伪标签的方法(将没有标签的数据的损失函数也加入进来，就是最后公式后边那一坨，具体如下图)

论文介绍

核心思想

Pseudo-Label 模型作为一个简单、有效的半监督学习方法早在 2013年就被提出，其核心思想包括两步：

• 第一步：运用训练出的模型给予无标签的数据一个伪标签。方法很直接：用训练中的模型对无标签数据进行预测，以概率最高的类别作为无标签数据的伪标签
• 第二步：运用 entropy regularization(熵正则化化) 思想，将无监督数据转为目标函数的正则项(如下文公式)。实际中，就是将拥有伪标签的无标签数据视为有标签的数据，然后用交叉熵来评估误差大小

相关流程

使用有标签数据和无标签数据同时以有监督的方式训练预训练网络。对于无标签的数据，在每次权值更新时重新计算的伪标签，被用于与监督学习任务相同的损失函数计算（即每次权值更新时，都重新计算伪标签，并将该伪标签当作真是标签用于计算损失函数）。

相关函数

Denoising Auto-Encoder

去噪自动编码器是一种无监督学习算法，基于使学习的表示对输入模式的部分破坏具有鲁棒性的思想。该方法可以用于训练自动编码器，这些微分代数方程组（DAE）可以堆叠起来初始化深度神经网络：

$h_i=s({\sum }_{j=1}^{d_v}{W}_{ij}{\tilde{x}}_j+b_i)$
${\hat{x}}_j=s({\sum }_{i=1}^{d_h}{W}_{ij}{h}_i+a_j)$
● ${\tilde{x}}_j$是第 j 个输入值的损坏版本
● ${\hat{x}}_j$是第 j 个输入值的重构

自动编码训练在于最小化$x_j$ 和 ${\hat{x}}_j$重构误差（error）。对于二分类输入值，常用的重构误差选择是交叉熵：
$L(x,\hat{x})={\sum }_{j=1}^{d_v}-x_{j}log{\hat{x}}_j-(1-x_j)log(1-{\hat{x}}_j)$

模型整体的目标函数

$$y_i^{\prime }=\{\begin{array}{ll}1,& \text{if i=argmaxi′fi′(x)}\\ 0,& \text{otherwise}\end{array}$$

L公式左边是评估有标签数据的误差交叉熵，右边是评估伪标签数据的误差交叉熵

$L=\frac{1}{n}{\sum }_{m=1}^n{\sum }_{i=1}^{C}L(y_i^m,f_i^m)+\alpha (t)\frac{1}{n^{\prime }}{\sum }_{m=1}^{n^{\prime }}{\sum }_{i=1}^{C}L(y_i^{\prime m},f_i^{\prime m})$

● $n$ 是SGD中有标签数据的mini-batch大小
● $n^{\prime }$ 是SGD中无标签数据的mini-batch大小
● $f_i^m$ 是有标签数据中 m 个样本的输出集合
● $y_i^m$ 是有标签数据中 m 个样本的真实标签
● $f_i^{\prime m}$ 是无标签数据中 m 个样本的输出集合
● $y_i^{\prime m}$ 是无标签数据中 m 个样本的伪标签
● $\alpha (t)$ 是平衡它们的系数

为了平衡有标签和无标签之间的损失引入了$\alpha (t)$
$\alpha (t)$ 的合理调度对网络性能至关重要：
● 如果 $\alpha (t)$ 太大，甚至对有标记数据的训练也会产生干扰
● 如果 $\alpha (t)$ 太小，则无法获得来自未标签数据的好处
此外，期望通过缓慢增加 $\alpha (t)$ 的确定性退火过程，来帮助优化过程，以避免较差的局部极小值，从而使无标签数据的伪标签尽可能类似于真实标签。

$$\alpha (t)=\{\begin{array}{ll}0,& \text{t<T1}\\ \frac{t-T_1}{T_2-T_1}{\alpha }_f,& \text{T1≤t<T2}\\ {\alpha }_f,& \text{T2≤t}\end{array}$$
● ${\alpha }_f=3,T_1=100,T_2=600$

伪标签有效的原因

类间的低密度分离

这个世界是非黑即白的，什么是非黑即白？

假设现在有一大堆的data，有标注数据，有非标注数据，在两个类别之间会有一个明显的鸿沟。给一些标注数据，可以把边界分在上图右边的线，也可以把边界分在上图左边的线。但是考虑非标注数据，那么左边的边界会好一点，在边界处，两个类别的密度是低的（不会出现data）。

熵正则化

熵正则化是在最大后验估计框架中受益于无标签数据的一种手段。该方案通过最小化无标签数据的类别概率的条件熵，支持类间的低密度分离，而无需对密度进行任何建模。

$H(y|x^{\prime })=-\frac{1}{n^{\prime }}{\sum }_{m=1}^{n^{\prime }}{\sum }_{i=1}^{C}P(y_i^m=1|x^{\prime m})logP(y_i^m=1|x^{\prime m})$
● $n^{\prime }$ 是无标签数据的数目
● $C$ 是类别数目
● $y_i^m$是第 m 个无标签样本的未知标签
● $x^{\prime m}$ 是第 m 个无标签样本的输入向量
这个熵用于度量类间的重叠。随着类间重叠的减少，决策边界上的数据点密度降低。

MAP估计被定义为后验分布的最大化：
$C(\theta ,\lambda )={\sum }_{m=1}^{n}logP(y^m|x^m;\theta )-\lambda H(y|x^{\prime };\theta )$
● n 是有标签数据的数目
● $x^m$ 是第 m 个有标签样本
● $\lambda$ 是平衡两项的系数
通过最大化有标签数据的条件对数似然（第一项），并最小化无标签数据的熵（第二项），我们可以利用无标签数据获得更好的泛化性能。

就如上文相关流程中所说: pseudo label多是先用标注数据训练模型，然后在未标注样本上预测，筛选高置信的未标注样本再训练新模型，训练多轮直到模型效果不再提升，而这篇文章的实现其实是把未标注样本作为正则项的一部分。因为预测label和预测概率是相同模型给出的，因此最小化预测label的交叉熵，也就是最大化预测为1的class对应的概率值，和MinEnt直接最小化未标注样本交叉熵的操作一样。(在思考模块详细讲解个人想法)

实验结果

在实验中，研究人员用 MNIST 数据集进行了实验验证，并尝试了在有标签数据仅为100、600、1000和3000时的结果入下图所示：

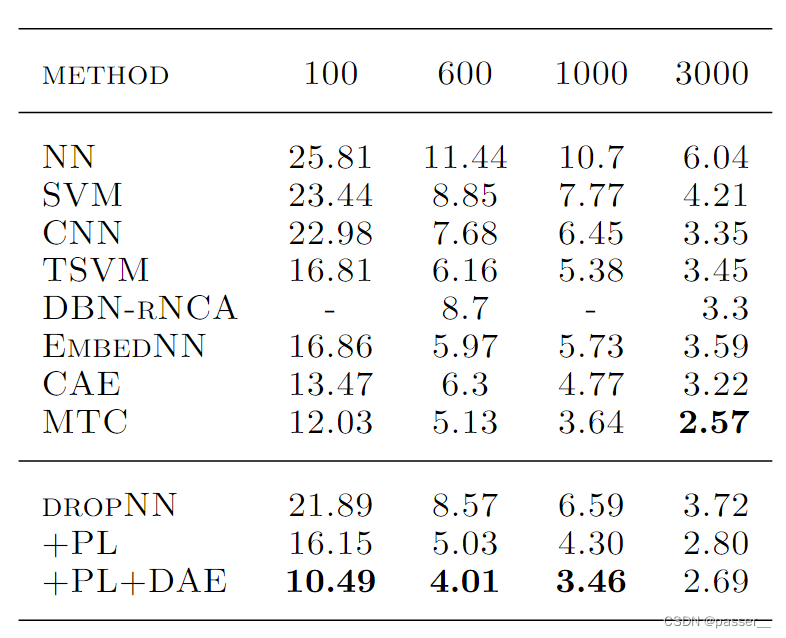
DROPNN、PL 和 PL+DAE 分别是实验中的 baseline 模型、baseline 模型+Pseudo-Label 方法 以及 baseline 模型+Pseudo-Label 方法+ DAE 预训练方案。

这里我们主要关注Pseudo-Label 方法的效果，其结果如表中倒数第二行所示。从表中可以看出，当有标签数据仅为 600 条时，Pseudo-Label 方法相对于其他公开模型，可以达到最佳的效果。但在其他实验条件下，只能实现相对较好的表现。不过相对于 baseline，此方法在所有情况下均能实现一定的提升。有标签数据量越少，这一提升越明显。这说明 Pseudo-Label 方法确实可以在一定程度上从无标签数据中提取有效信号。

进一步，研究人员通过降维可视化的方式展示了 Pseudo-Label 模型使用前后的效果，实验数据包含 600 有标签数据 + 60000 无标签数据：

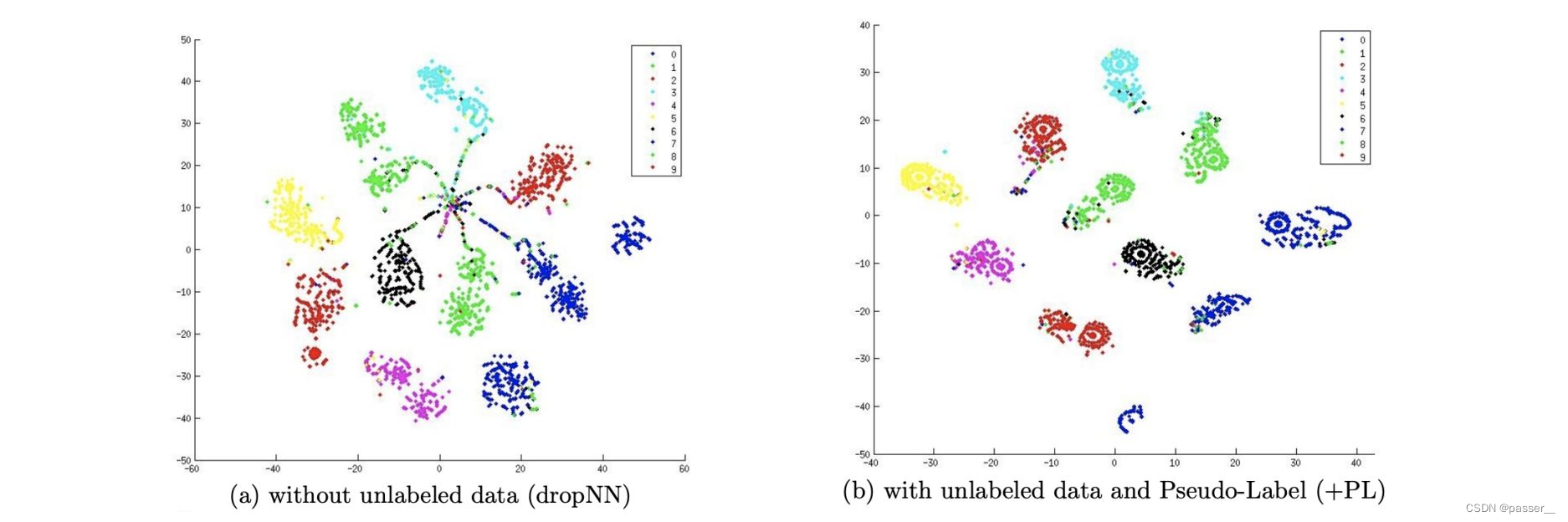
对比上面左右两张图可以看出来， Pseudo-Label 模型相对于单独的有监督模型，可以有效改善各类别数据在空间中的聚集密度。

读后感

思考

熵正则化的目的是为了让相同类别的分布更加集中，减少class overlap；而降低预测值和伪标签的交叉熵，也就是最大化预测为1(或者一个类的概率非常接近1，可以近似等于1？)的class对应的概率值,也就是让最有可能的预测结果最大，这样的话信息熵自然就很小。

存在不足

Pseudo-Label 方法只在训练时间这个维度上，采用了退火思想，即采用时变系数α(t)。而在伪标签这个维度，对于模型给予的预测标签一视同仁，这种方法在实际中存在明显问题。很显然，如果模型对于一个样本所预测的几个类别都具有相似的低概率值，如共有十个类别，每个类别的预测概率值都接近 0.1，那么再以最大概率值对应的类别作为伪标签，是不合适的，将会引入很大的错误信号。(概括一下也就是：Pseudo-Label 方法，以最大概率值对应的类别作为伪标签这个操作是不太合适的(考虑到每个类别的预测概率值都接近 0.1，每个类别的预测结果都很差))

本文内容参考如下:
伪标签（Pseudo-Labelling）——锋利的匕首

我们真的需要那么多标注数据吗？半监督学习技术近年来的发展历程及典型算法框架的演进

[论文笔记]Pseudo-Label：The Simple and Efficient Semi-Supervised Learning Method for Deep Neural Networks

Pseudo-Label : The Simple and Efficient Semi-Supervised Learning Method for Deep Neural Networks

Pseudo-Label 代码