本文主要是介绍三个两两垂直而且两两相切的圆柱面的最小公共切球面的半径，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！
问题来源
2016年江苏省高中数学冬令营填空题。
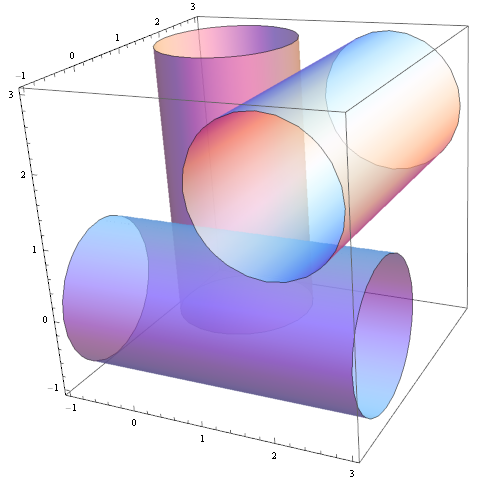
三个底面圆半径都是1的圆柱面，两两相切、两两垂直。求跟它们都相切的最小球面的半径。
如果利用高等数学一些的观点，容易发现半径是 2√−1 。——从没有太多约束的更宽的视野看看初等数学问题，可能更容易显出学习高等一些数学知识的意义或趣味。
高等解法
思路：
找到三个圆柱面中轴线距离平方之和最小的点，这个点是要求的球面的球心；而且已经有线性算法。链接虽然只提到了两条直线的情形，但是可以容易推广到任意 n 条时候。
然后就是求三维空间点到直线的距离的问题了。由于三个圆柱之间的关系，并无特殊性，所以，到每个圆柱中心线的距离相等。用这个距离
简单求解
假设如图所示的三个简单圆柱面：
容易找出确定它们各自的中心线所需的固定点的向量 Xi 和表示其方向的单位向量 Wi (i=1,2,3) 。
Xi 为下面矩阵的各列：
⎡⎣⎢000202020⎤⎦⎥(1)
这篇关于三个两两垂直而且两两相切的圆柱面的最小公共切球面的半径的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！
