Lie theory for the roboticist

Reference:

1. A micro Lie theory for state estimation in robotics
2. 机器人学——李群、李代数快速入门

1. Introduction

1.1 $S^1$：单位复数

首先进入第一个例子来讨论复平面、单位复数以及它们旋转向量的能力。我们知道如果将复数 x 乘以一个单位复数 z，z 作用在 x 上的结果是使 x 旋转并等于 y。这里 z 就是这篇文章需要关注的重心：z 是单位复数的成员，而单位复数是李群最简单的例子之一。

• 复数需要在复平面上施加约束 $z^{\ast }\cdot z=1$，相当于在 z 上施加了一个单位范数；
• 这时满足该约束的点的形状构成了一个拓扑图形：该形状是圆，也可以看成是一维的线------这就是复平面中的一个单位圆；
• 该单位圆的元素可以写成：$z=\cos \theta +i\sin \theta$。这里 $\theta$ 正是 x 绕 z 旋转的角度；
• 该复数的逆为其共轭复数 $z^{\ast }$；
• 也可以通过使用复数的乘积运算来组合不同的操作符。

以上这些内容都是李群的经典部分，现在我们切换到其他的李群，即二维的旋转矩阵：

1.2 SO(2)：二维旋转矩阵

这时可以注意到，上面关于复数的一切解释在此都适用。因此有两个东西是需要分清的：

1. 运算符(operator)：在这里是旋转矩阵；
2. 该运算符所作用的元素。

Okay，现在知道了这两个东西，我们想将这两个东西，即产生旋转的主体和被旋转的元素分开。李群是这个图像的左侧部分，可以变换其他在右侧集合中的元素。这里可以清楚地看到，x 不是旋转矩阵：向量 x 只是一个向量，而 R 能够旋转 x。

1.3 $S^3$：单位四元数

这种区分是非常有必要的，因为如果现在跳到另一个李群，即单位四元数组，这时候就不再能够在与左侧组相同的绘图中绘制旋转向量。这篇文章的主要关注点在这张图左侧，即群本身，而不是右侧元素在被群转换时的几何表示。

1.4 典型使用：

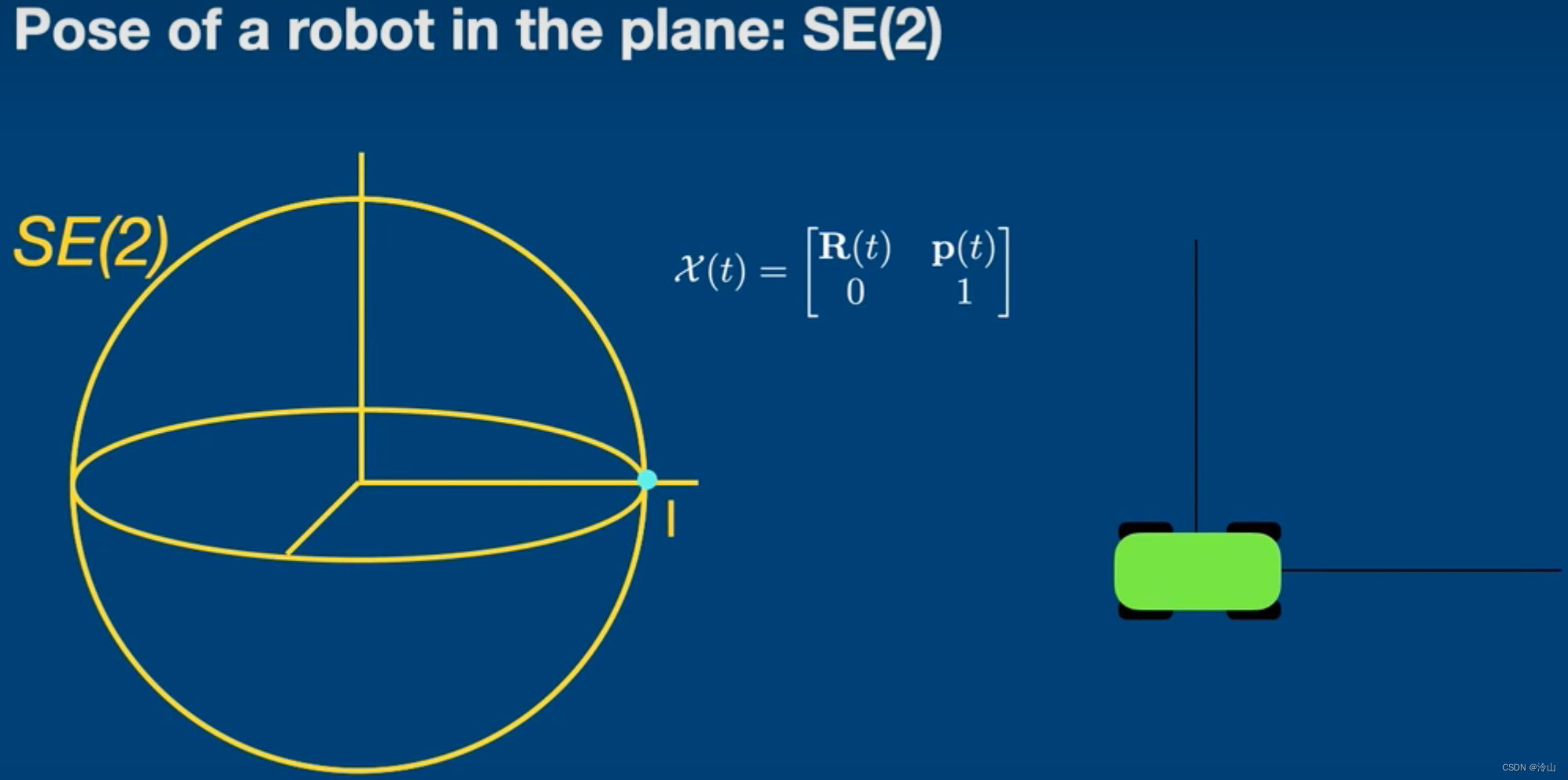
另一个可以很好分离这两个概念的图像，是例如像上图平面中的一组刚体运动----它由平移和旋转组成，这就是SE(2)群。可以看到一个点在群的表面上移动时，右侧物理表示为一个在平面上移动的机器人，我们将平面上的这种运动抽象为在球体上移动的点的运动，称之为表面上的流形(manifold)。

1.5 更复杂的情况

也可以使用它处理更复杂的情况：例如类人机器人许多关节在$3$维空间中移动，因此每个关节都可以由SE(3)群的一个元素表示。

1.6 为什么选择李群

因为群是一种抽象和有原则的方式，可以用这些对象做很多事情。其中一些刚刚已经看到了，如组合和取逆；还可以在两个元素进行插值、对其他对象产生变换(平移、旋转等)；更重要的是，由于李理论，我们可以对这些物体进行微积分，所以我们可以进行积分和微分，比如构造雅可比矩阵等等。因此，可以以一种非常优雅和良好的方式处理不确定性。所有这些都使我们能够构造真正强大的规划控制等算法。大多数概念是可以被抽象的，但不是所有都可以被抽象。

2. 李群(Lie group)的定义

2.1 公理

什么是群？群是一些元素组成的集合，例如含有元素 { X , Y , Z } \{X,Y,Z\} {X,Y,Z} 的集合 $G$，它群通过四个公理定义。(这里十四讲讲的完全一样)

1. 群带有一些运算，被称为封闭性(Composition)，即两个元素的组合得出的一个元素也在该群中；
2. 存在这样的一个元素-----单位元素(Identity element) ，当我们用任何其他元素与单位元素进行操作时，我们所得到的都是该元素本身；
3. 群内有一个逆元素(Inverse element)，当我们用其逆元素操作元素时，我们会得到单位元素；
4. 还有一种组合操作时结合律(Associative).

还有很重要的一点是，正如在上图最后一行中看到的那样，几乎所有的这种 . 的组合操作是不可交换的。例如，我们知道$3$维空间中的旋转是不满足交换律的，但$2$维空间中的旋转是可交换的。

2.2 李群的定义

定义：李群是一个群，同时也是一个光滑的流形。为了理解这句话，首先来了解以下什么是光滑的流形：

流形就像一个空间中的超表面，它是光滑的，这意味它没有棱边(edge)或尖峰(spikes)，我们要处理的是光滑的表面。

李群的现代定义：李群是一个其元素满足上述的四个群公理的光滑的流形。

2.3 群和作用集

引入群的第三个概念是通过它的作用。对于一个单独的群，也许其自身并不需要一种操作，但是我们使用群是因为它们具有改变其他元素的能力。比如上面提到过的，使用旋转矩阵来旋转向量----这不单纯是为了计算这些旋转矩阵本身，还是为了旋转其他元素。所以旋转这个概念是随着群的概念出现的。事实上，李群在上个世纪初被称为连续变换群。(SE(3)?)

它也有两个公理：

1. 如果用单位元素操作另一个集合中的元素，这个元素不会改变；
2. 如果首先将该集合的两个元素组合起来，然后对向量 $v$ 进行操作，这与首先以同样的方式改变 $Y$ 元素，然后再对另一个元素进行操作是一样的。

3. 李理论的拓扑-----流形、切空间及指数映射

现在让我们谈谈李理论的拓扑。从几何上讲 ，具有群流形、切空间和指数映射：

上图的球体代表了一个特殊的李群流形。在介绍单位复数 x 之前，这里引入一个代表四元数的单位圆的球体，它是一个嵌入四维空间中某个球形的三维表面，这是一个四元数群----这是关于流形的。

• 在这个流形的一个点上，我们可以找到群的一个单位元素(identity element)(即上文的 $E$)，这在复数内为 $1$，也是旋转矩阵的单位矩阵。在这个点上我们可以建立一个线性的切线空间，并在这一点上与流形相切，所以我们可以在任何点放置切线。在单位点的某个特殊切空间称为李代数。
• 在李代数上，我们可以定义一些向量，这些向量当然与流形的这个单位点相切。可以在图中看到绿色、蓝色和黄色的切向量(tangent vector)在图中均为一条线，可以尝试将这条线绕到球体表面上，这种缠绕遵循我们所谓的测地线(geodesic)，这是流形中可能的最大弧，所以把这条线折叠到流形上的操作，称为指数映射(exponential map)。这是一个映射，它从切线空间提取一个向量，然后产生群的一个元素。而由对数映射(logarithmic map)执行逆映射。(是不是可以理解成，在单位点的特殊切空间称为李代数，而其他的点就是切空间，而不能表示李代数)

3.1 切线空间和李代数

• 显然切线空间是线性的，并且与流形相切，因为流形没有尖峰或类似的东西，所以它很平滑，每个点上都具有独属的切线空间；
• 因为它是一个向量空间，我们可以对它使用微积分。
• 切线向量空间的维数等于流形的自由度；
• 正如前面说的，在单位点的切线空间称为李代数。(注意是单位点，其他点的切空间并不能表示成李代数(肯定))

3.1.1 $S^1$ 的切空间

让我们看看这个切空间的结构以线性形式呈现出什么样子，为了这个目的，我们现在施加给群以约束，这里主要以单位复数为例：

施加约束 $z^{\ast }\cdot z=1$，并分别对时间微分，得 ${\mathbf{z}}^{\ast }\dot{\mathbf{z}}=-{\left({\mathbf{z}}^{\ast }\dot{\mathbf{z}}\right)}^{\ast }$，这时就得到一个对象完全等于它的共轭的负数。这个在复平面中，只有当该对象是虚数时才能完成，因此 $z^{\ast }\dot{z}$ 是虚数，因此可以将其写成 $i\ast \omega$，而 $\omega$ 在实数域。(因为 $z^{\ast }$ 为 $z$ 的逆，公式写成 $\dot{z}=i\omega z$ 就好理解多了)

所以我们定义李代数是虚数的空间(再强调一下，在单位点的切线空间才称为李代数)，也可以把这个空间看作是虚数的一堆线，但我们可以用实数完美地编码它(Cartesian坐标)，所以无论如何它都是一条线。所以如果我们有 $i$ 和 $\omega$，或者知道 $\omega$ 表明知道相同的信息。所以有两种方式表示这个切线空间，且这些方法是同构的(Isomorphism)。

李代数中有一运算符，它被称为帽子运算符(hat operator)，这时 $\omega \hat{}=i\cdot \omega$，$\omega$ 为实数；反之 $\omega =-i\cdot {\omega }^{\vee }$。

3.1.2 SO(3) 的切空间

同样的事也会发生在三维旋转上，相比前面会稍微复杂一点。
可以对约束条件应用相同的微分 $R^T\cdot R=I$，最终得到 ${\mathbf{R}}^{\top }\dot{\mathbf{R}}=-{\left({\mathbf{R}}^{\top }\dot{\mathbf{R}}\right)}^{\top }$，这意味着 ${\mathbf{R}}^{\top }\dot{\mathbf{R}}$ 是一个反对称矩阵，并且 3x3 反对称矩阵具有三个自由度，因此李代数也具有三个自由度，而三维空间中旋转矩阵的正切空间是一个三维线性空间。
这里再稍微强调一下，这个反对称矩阵形成的代数结构，是由三维坐标里三个基本元素线性组成的，可以将这些坐标转换为正则向量，并且这个切线空间由笛卡尔(Cartesian)坐标系表示。这时可以注意到有一个切线空间，也可以同时用两种不同的方式 ${\omega }^{\wedge }={\omega }_x$ 和 $\omega ={{\omega }_x}^{\vee }$ 来表示。

在许多领域中，使用向量比使用奇怪的对象（如反对称矩阵或虚数）更易操作。因此，在各种集合里，我们能够将切向量元素表示为笛卡尔向量。如有必要，这些向量可以堆叠在更大的向量组中。非常重要的是，这些向量可以用矩阵代数来进行操作。

4. 指数映射

正如前面所提到的，指数映射是从切空间到流形的映射，或者使用对数映射从流形到切空间。

现在来看看它是如何工作的：
采用前面的方程，$\dot{\mathbf{R}}=\mathbf{R}\cdot {\omega }_{\times }$(这个和 $\dot{\mathbf{R}}={\omega }_{\times }\cdot \mathbf{R}$ 是一个东西，只是前面推导时用的 $R^{T}R=I$ 而不是 $R{R}^T=I$)，对这个微分方程积分，结果是 $\mathbf{R}(t)={\mathbf{R}}_0\cdot \exp \left({\omega }_{\times }t\right)$。这里的指数在原点处的矩阵 $R_0$ 等于单位点，这时有 $\mathbf{R}(t)=\exp \left({\omega }_{\times }t\right)=\exp \left({\theta }_{\times }\right)$。实际上 $\omega$ 是旋转速率，$t$ 是时间，其乘积只是一个角度，用 ${\theta }_{\times }$ 表示。

关于如何找到这个指数的闭环表达式，只需写出其泰勒展开，最终得到 $\left[\begin{array}{cc}\cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{array}\right]$ (这里的推导写的有点问题，但结果是对的)，也就是一个旋转矩阵。
因此 $\exp \left({\theta }_{\times }\right)$ 就是 $R(t)$，而相反的方式是对数映射。我们可以直接从笛卡尔坐标系出发构造指数映射，即直接从 $Exp(\theta )\to R$，这时将两种指数映射区分开来，右边的方式使用大写的 Exp 和 Log。

4.1 大写的指数映射

图中左侧可以看到切线空间的两种表示方式，右侧为流形，里面有所有将一个地方转换到另一个地方的映射。

5. 加和减运算符

这里介绍另一个快捷方式，它是一个运算符，它将群的组成(Composition)和指数映射结合到了一起。这允许取一个元素 $\mathcal{X}$ 并在它上面添加另一个切空间元素 $\omega$ 的指数。这也可以被叫 $\mathcal{X}$ plus($\oplus$) $\omega$。
同样也存在 minus($\ominus$) 运算符，它使用两个群的元素，并表达其差异作为切线空间的元素，在上面示例中为在 $\mathcal{X}$ 处的点。

论文中反应的比较清楚，这里左边表示的李代数，右边表示的是切空间+李代数，这里李代数写的是 $\exp (i\theta )$，进一步说明只有在单位点的切空间才称为李代数。

6. 伴随矩阵(Adjoint matrix)

现在使用这两个运算符，可以用图形方式表示群的伴随。
想象有图上画这个流形 $\mathcal{M}$，有单位点 $\mathcal{E}$ 和一个点 $\mathcal{X}$，用两种方式表达一个点 $\mathcal{Y}$，即 $\sigma \oplus \mathcal{X}$ 或 $\mathcal{X}\oplus \tau$。两式相等，可得 $\exp ({\sigma }^{\wedge })=\mathcal{X}\cdot \exp ({\tau }^{\wedge })\cdot {\mathcal{X}}^{-1}$，可知 $\tau$ 和 $\sigma$ 之间的关系是线性的，如果像后面 $\sigma ={\mathbf{Ad}}_{\mathcal{X}}\cdot \tau$ 这样的笛卡尔形式写，也别忘了 $\sigma$ 和 $\tau$ 是流形的切向量。$\mathcal{X}$ 处的伴随是将 $\tau$ 转换为向量 $\sigma$ 的矩阵，所以伴随矩阵是一个线性算子，它将流形点 $\mathcal{X}$ 处的切空间的元素映射到了单位点 $\mathcal{E}$ 处的切空间的元素。

7. 李群的微积分及雅克比

现在进入李理论的微积分，在这里使用向量的笛卡尔表示，以表示变量的扰动、误差、增量等，因此接下来将可以看到涉及来自一个流形的元素的雅克比函数，转换到另一个流形的元素；我们也可以定义和操作协方差，从而以优雅的方式处理不确定性。
首先让我们看看如何定义一个雅克比矩阵，或者说导数。上图左侧可以看到经典的在向量空间经典的导数公式，现在在右侧使用新的加减运算符替代左侧的加减号，并以这种方式定义导数。

这是非常相关的，现在再看看如何计算它们，这时我们所做的是应用定义并尝试将分子限制到线性形式，并得到最终的雅克比。

我们来看一个例子，想象有一个三维旋转的函数，所以这个函数需要一个矩阵 $R$(SO(3)) 和一个点 $p$(${\mathbb{R}}^3$)，施加 $R$ 在 $p$ 上，现在需要计算这个函数的导数。

首先是关于矩阵 $R$ 的导数，所以这意味着什么？据矩阵有九个数字，但只有三个自由度。所以这个导数做的是计算相对于输入自由度的输出变化。这意味着在切线空间的输出变化表示和在切线空间的旋转矩阵输入变化是三维的，所以 $\frac{Df}{DR}$ 实际上是一个三乘三矩阵，只需按照几个步骤就可以很容易的计算出来。

相同的过程也可以求旋转相对于点的导数。

如上所示，雅克比将切向量从输入流形 $\mathcal{M}$ 映射到输出流形 $\mathcal{N}$ 上的切向量。这就是为什么它是雅克比矩阵，因为它将向量转换为向量。

7.1 李群的微分规则

8. 李群的扰动

一般来说在 $x$ 上的扰动，我们在 $\mathcal{X}$ 处的切线空间上表达它，所以我们可以说扰动元素 $\mathcal{X}$ 等于未扰动的 $\bar{\mathcal{X}}$ 加上扰动 $\tau$。

这种方式非常实用，因为我们可以定义 $\mathcal{X}$ 的协方差，这实际上是 $\tau$ 的协方差，所以我们只需放置 $\tau$ 的协方差，并用其表达式替换 $\tau$，即使用 $(\mathcal{X}\ominus \overline{\mathcal{X}})$ 替换 $\tau$，它与常规协方差定义几乎相同。

使用这个公式并使用先前的雅克比公式，现在恢复了众所周知的传播不确定性的方式。函数 $\mathcal{Y}$ 等于 $f(\mathcal{X})$，还有雅克比 $\mathbf{J}=\frac{D\mathcal{Y}}{D\mathcal{X}}$。要将 $f(\mathcal{X})$ 上的协方差转换为 $f(\mathcal{Y})$ 上的协方差，只需像往常一样左右乘雅克比就行。

9. 李群的积分

最后一点是积分。
正如所说的，在连续时间中，恒定速度的指数积分为一个李群。对于离散时间，只需将速度分解为一段段的恒定轨迹，然后使用加号运算符来创建轨迹。

10. 应用

最后再来讲两个估计领域的例子。
该例子设计一个移动机器人，正在观察一个数字环境中的路标。该例子是基于 EKF 的地图定位系统，这时我们有机器人的位姿(SE(3))。

可以使用上一张图中的积分表示运动模型；也可以编写测量模型，那么怎么做我们从位姿 $\mathcal{X}$ 对路标 b 进行测量。现在我们构建了EKF的预测阶段和矫正阶段。在这里不会讲授关于EKF的课程，但想注意的是，这些方程与在经典EKF中使用的大致相同，但也有很多不同之处的：
首先是协方差被定义在元素的切空间上，所以在旋转矩阵的情况下，此协方差是三维的，因为切线空间是三维的。因此 $P$ 是一个 3*3 的矩阵。
我们有运动积分公式，有切空间因为我们正在对速度进行积分并且速度与它正在移动的任何东西相切，所以这属于切空间。
我们有逆算子、action、有映射到切空间的雅克比的计算方法，最后我们更新了卡尔曼滤波器状态，它正在使用加运算符 $\hat{\mathcal{X}}\oplus \mathbf{K}{\mathbf{z}}_k$。

除此之外，它的外观和常规EKF几乎相同。
第二个示例使用平滑和映射，所以要使用列表方块技术来解决类似的问题。在这种情况下机器人和路标的姿态是未知的，我们将状态向量封闭到一个李群内 $\mathcal{X}=⟨{\mathcal{X}}_1,{\mathcal{X}}_2,{\mathcal{X}}_3,{\mathbf{b}}_4,{\mathbf{b}}_5,{\mathbf{b}}_6⟩$，即三个位姿加三个路标的组合，这时对最小而成问题优化。我们写下了测量构建来构建雅克比矩阵和最终的残差，并计算牛顿更新状态并迭代这个非线性系统。再一次的，在这里需注意加减运算符以及雅克比的使用作为我们定义它们的方式。