Game Theory In Competitive Programming|Part2（原创）

本文主要是介绍Game Theory In Competitive Programming|Part2（原创），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

在上一个Part部分，我们介绍了Bash game、Nim game、Misere Nim game 这三个游戏的玩法、必胜策略，以及必胜策略的证明，并介绍了有关必胜态以及必败态的两条定理，接下来我们会以Part1为基础，深挖其中的理论。

文章目录

- 1、Grundy Numbers/Numbers and Mex的引入
- - - - 定义Mex
      - 定义运算Mex(set)
- 2、Sprague-Grundy Theorem
- - - - Sprague-Grundy Theorem是什么
      - 应用S-G Theorem
- 3、Practice
- - - - Game1
      - Game2
      - Game2.1
      - Game3

1、Grundy Numbers/Numbers and Mex的引入

$G r u n d y N u mb ers$ 是一种在组合游戏理论中用来分析游戏局势的数学概念。

它主要用于判断在一些特定游戏中，当前局面对先手玩家是有利的还是不利的。

具体地说，给定一个游戏状态或局面， $G r u n d y$ 数能表示这个局面的胜负情况。

定义如下：

1、如果一个局面是终止局面，其 $G r u n d y$ 数为 $0$ 。

2、对于非终止局面，其 $G r u n d y$ 数定义为所有可能的下一步局面的 $G r u n d y$ 数中最小未出现的非负整数。

设当前状态为 $S$ ，其进行一次合法操作后的可能状态集合为： $\lbrace S_1,S_2,...S_k\rbrace$

则有: $Grundy(S)=Mex(\lbrace Grundy(S_1),Grundy(S_2),...,Grundy(S_k)\rbrace)$

定义Mex

集合中未出现的最小非负整数。

定义运算Mex(set)

求出集合中未出现的最小非负整数。

列表观察：

Mex(set)	结果
Mex( $\emptyset$ )	0
Mex({1,2,3})	0
Mex({0,2,3,4})	1
Mex({0,1,2,3,4,…, $w$ })	$w + 1$

下面用几个简单的游戏来验证 $G r u n d y$ 数：

Game1

题目：

有一堆数量为 $n$ 的石子，两个人轮流操作，每次操作可以取走任意数量的石子（不能不取）。

取走最后一个石子的玩家获胜。

列表观察 $0\sim10$ 的Grundy Numbers：

$Grundy(0)=Mex(\empty)=0$

$Grundy(1)=Mex(\lbrace Grundy(0)\rbrace)=1$

$Grundy(2)=Mex(\lbrace Grundy(0),Grundy(1)\rbrace)=2$

$...$

$Grundy(n)=Mex(\lbrace Grundy(n-1),...,Grundy(0)\rbrace)=n$

N	0	1	2	3	4	5	6	7	8	9
Grundy(N)	0	1	2	3	4	5	6	7	8	9

观察到，只有 $n = 0$ 的时候Grundy Numbers = 0 , 所以 $n = 0$ 的时候先手必败。

否则先手必胜。

这显然和我们的结论是一样的。

Game2

题目：

最初有一堆数量为 $15$ 的石子，选手甲、乙交替操作，每次操作需要从石子堆中拿走不超过 $3$ 个石子。

甲先手操作，取走最后一个石子的选手获胜。请问最终谁获胜？

只需要求解出每个状态的Grundy数即可。

$Mex(\empty) = 0.$

$Mex(\lbrace Grundy(0)\rbrace) = 1.$

$Grundy(2)=Mex(\lbrace Grundy(0),Grundy(1)\rbrace)=2.$

$Grundy(3)=Mex(\lbrace Grundy(2),Grundy(1),Grundy(0)\rbrace) = 3$

$Grundy(4)=Mex(\lbrace Grundy(3),Grundy(2),Grundy(1)\rbrace)=0$

$...$

$Grundy(15)=Mex(\lbrace Grundy(14) ,Grundy(13),Grundy(12)\rbrace)=3$

在这个游戏中，如果把 $15$ 换成 $n$ 也是一样能够求解的，我们可以通过线性递推的方式求解出Grundy(n).

如果 $G r u n d y (n) = 0$ 即代表这是一个必败态。

N	0	1	2	3	4	5	6	7	8
Grundy(N)	0	1	2	3	0	1	2	3	0

这显然符合 $\:game$ 的结论。

Game3

题目：

最初有一堆数量为 $10$ 的石子，选手甲、乙交替操作，每次操作可以将石子的数量除以2、3、6，并向下取整。

甲先手操作，最后一次操作的人获胜。请问最终谁获胜？

$G r u n d y (0) = 0$ .

$Grundy(1)=Mex(\lbrace Grundy([\frac{1}{2}]),Grundy([\frac{1}{3}]),Grundy([\frac{1}{6}])\rbrace) = Mex(\lbrace0,0,0\rbrace)=1$

$Grundy(2)=Mex(\lbrace Grundy([\frac{2}{2}]),Grundy([\frac{2}{3}]),Grundy([\frac{2}{6})]\rbrace) = Mex(\lbrace1,0,0\rbrace)=2$

$Grundy(3)=Mex(\lbrace Grundy([\frac{3}{2}]),Grundy([\frac{3}{3}]),Grundy([\frac{3}{6})]\rbrace) = Mex(\lbrace1,1,0\rbrace)=2$

$Grundy(4)=Mex(\lbrace Grundy([\frac{4}{2}]),Grundy([\frac{4}{3}]),Grundy([\frac{4}{6})]\rbrace) = Mex(\lbrace2,1,0\rbrace)=3$

$...$

$Grundy(6)=Mex(\lbrace Grundy([\frac{6}{2}]),Grundy([\frac{6}{3}]),Grundy([\frac{6}{6})]\rbrace) = Mex(\lbrace3,2,1\rbrace)=0$

$=0(n\geq6)$

列表有：

N	0	1	2	3	4	5	6	7	8
Grundy(N)	0	1	2	2	3	3	0	0	0

2、Sprague-Grundy Theorem

Sprague-Grundy Theorem是什么

$S - G$ 定理是一个解决类似于 $N im$ 的公平组合游戏的通法。

我们把单个 $N im$ 堆上的游戏对局叫作一个子对局。

而 $S - G$ 定理的内容是：假设有 $N$ 个子对局和两个棋手 $A 、 B$ 组成的综合对局，

如果 $A 、 B$ 都按照最优策略下棋，那么在对局开始之前就能判断输赢。

各个子对局的 $G r u n d y$ 数异或和为 $0$ ，先手必败。

各个子对局的 $G r u n d y$ 数异或和不为 $0$ ，先手必败。

应用S-G Theorem

将综合对局分解为一个个子对局。
对于每一个子对局计算其 $G r u n d y$ 数。
计算所有子对局的 $G r u n d y$ 数的异或和。
如果异或和为 $0$ ，那么先手必败，否则先手必胜。

3、Practice

Game1

题目：

初始时有三堆石子，每一堆分别有 $3 、 4$ 和 $5$ 个石子。

甲乙交替操作，每次操作可以取一堆石子中的 $1\sim3$ 个。

取走最后一个石子的玩家获胜，请问最终谁会获胜？

$S-G\:Theorem:$

这个游戏可以分解为3个子游戏，每一个子游戏分别有 $3 、 4 、 5$ 个石子。
可以计算出每个子游戏的 $G r u n d y$ 数 : $3 、 0 、 1$ 。
计算出子游戏 $G r u n d y$ 数的异或和 $:$ 2。
得出结论：先手必胜。

Game2

题目：

给一个迷宫，迷宫内有空地和障碍物(蓝色格子)，棋子在右下角。

甲乙交替操作，每次操作只能将棋子向上或向左移动任意单位长度（不能不移动）。

最后移动的玩家获胜。

迷宫的初始状态如下图：

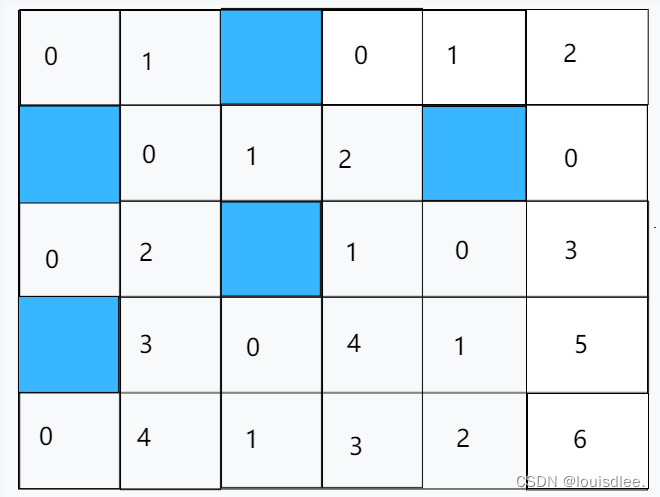
在这里插入图片描述

我们可以对每个位置，都求出其 $Grundy\: Number$ ，结果如下图：

在这里插入图片描述

如果初始位置的 $G r u n d y$ 数是 $0$ ，那么根据 $S - G$ 定理：先手必输。

如果初始位置的 $G r u n d y$ 数非 $0$ ，根据 $S - G$ 定理：先手必胜。

Game2.1

题目：

假如给定三个迷宫，每次操作都能选择一个迷宫，并操纵里面的棋子向上或向下走任意距离。

棋子在右下角，最终无法进行操作的人输。

题中迷宫如图：

在这里插入图片描述

可以求出每个迷宫的 $G r u n d y$ 数如下图：
在这里插入图片描述

注意到初始状态下，三个子状态的 $Grundy\:Number$ 异或和为 $2\bigoplus 3\bigoplus 3=2$

所以先手必胜。

Game3

题目：

最初有一个数量为 $n$ 的石子堆，甲乙轮流进行操作。

每次操作可以选择场上任意一堆石子，并将这堆石子分为石子数量不相同的两堆石子(不能为 $0$ )。

不能进行操作的人输。

我们假设 $n = 8$ ，模拟这场游戏来观察规律：

1、 $n = 1$ ，显然这一堆石子无法继续分， $G r u n d y (1) = 0$ .

2、 $n = 2$ ，显然这堆石子无法分为数量不相同的两堆石子， $G r u n d y (2) = 0$ .

3、 $n = 3$ ，这堆石子可以分成 $(1, 2)$ 。 $Grundy(3)=Mex(\lbrace Grundy(2)\bigoplus Grundy(1)\rbrace)=1$ .

这也代表着， $n = 3$ 的石子可以分裂出两个子游戏

这两个子游戏的胜负会影响父游戏的胜负，所以需要用到 $S-G\:Theorem:$

一个游戏若是能分解为若干子游戏，那么这个游戏的结果取决于子游戏的 $Grundy\: Number$ 异或和

故 $Grundy(3)=Mex(\lbrace Grundy(2)\bigoplus Grundy(1)\rbrace)=1$