本文主要是介绍卡尔曼滤波(Kalman Filter,KF)基础推导及其实例,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
文章目录
- 卡尔曼滤波(Kalman Filter,KF)
- 涉及到的主要知识
- 卡尔曼滤波中涉及的几个常用概念
- 卡尔曼滤波中最重要的五个公式
- 卡尔曼增益的推导
- 后验估计表达式的推导
- 误差协方差矩阵的推导
- 卡尔曼滤波在控制领域应用的推导
- 卡尔曼增益详解
- 卡尔曼增益的计算方式
- 卡尔曼增益的解读
- 卡尔曼滤波的应用
- 普通应用中的一般流程
- 实例说明
- 应用实例(matlab):预测实际硬币的直径
卡尔曼滤波(Kalman Filter,KF)
自用笔记,带一些个人理解和知识拓展,详见b站Dr.CAN卡尔曼滤波专题,权侵删
本篇为卡尔曼滤波入门介绍,推导基于线性控制系统,但使用例子为测量硬币真实直径
涉及到的主要知识
- 线性代数
- 概率论
- 矩阵论
- 最优估计
卡尔曼滤波中涉及的几个常用概念
- 先验估计:通过理论公式计算得到的,无干扰情况下理论的输出值
- 卡尔曼增益:通过概率论知识,估计出对理论输出值的实际输出误差补偿
- 后验估计:理论计算+综合考虑了干扰影响后的实际输出值(通过概率对误差进行估计,然后反馈补偿到理论输出值上)
卡尔曼滤波中最重要的五个公式
已知:实际控制系统中存在过程噪声 w w w和测量噪声 v v v,它们均符合高斯分布,分别写作
{ x k = A x k − 1 + w k − 1 z k = H x k + v k { w ∼ p ( 0 , Q ) v ∼ p ( 0 , R ) \begin{cases} x_k = Ax_{k-1}+w_{k-1}\\ z_k = Hx_k + v_k \end{cases}\\ \begin{cases} w \sim p(0,Q)\\ v \sim p(0,R) \end{cases} {xk=Axk−1+wk−1zk=Hxk+vk{w∼p(0,Q)v∼p(0,R)
式中 0 0 0表示两种噪声的期望值, Q Q Q和 R R R分别表示两种噪声分布的方差。
经过推导,得到以下五个重要公式
先验估计: x ^ k − = A x k − 1 先验误差协方差: P k − = A P k − 1 A T + Q 卡尔曼增益: K k = P k − H T H P k − H T + R 后验估计: x ^ k = x ^ k − 1 + K k ( z k − x ^ k − 1 ) 更新误差协方差: P k = ( I − K k H ) P k − \begin{split} 先验估计:\hat x_k^- &= Ax_{k-1}\\ 先验误差协方差:P_k^- &= AP_{k-1}A^T + Q\\ 卡尔曼增益:K_k &= \frac{P_k^-H^T}{HP_k^-H^T + R}\\ 后验估计:\hat x_k &= \hat x_{k-1}+K_k(z_k - \hat x_{k-1})\\ 更新误差协方差:P_k &= (I - K_kH)P_k^- \end{split} 先验估计:x^k−先验误差协方差:Pk−卡尔曼增益:Kk后验估计:x^k更新误差协方差:Pk=Axk−1=APk−1AT+Q=HPk−HT+RPk−HT=x^k−1+Kk(zk−x^k−1)=(I−KkH)Pk−
卡尔曼增益的推导
已知两个相互独立事件的目标发生概率分别为 σ 1 \sigma_1 σ1和 σ 2 \sigma_2 σ2,求其联合概率 σ Z ^ \sigma_{\hat Z} σZ^。求 K k K_k Kk促使 σ Z ^ \sigma_{\hat Z} σZ^的不确定性最小,即求方差 v a r ( Z ^ ) var(\hat Z) var(Z^)最小值,此时即为最优解,推导过程如下
σ Z ^ 2 = v a r [ Z 1 + K k ( Z 2 − Z 1 ) ] = v a r ( Z 1 − K k Z 1 + K k Z 2 ) = v a r [ ( 1 − K k ) Z 1 + K k Z 2 ] = v a r [ ( 1 − K k ) Z 1 ] + v a r ( K k Z 2 ) = ( 1 − K k ) 2 v a r ( Z 1 ) + K k 2 v a r ( Z 2 ) = ( 1 − K k ) 2 σ 1 2 + K k 2 σ 2 2 \begin{split} \sigma_{\hat Z}^2 &= var[Z_1+K_k(Z_2-Z_1)]\\ &=var(Z_1-K_kZ_1+K_kZ_2)\\ &=var[(1-K_k)Z_1+K_kZ_2]\\ &=var[(1-K_k)Z_1]+var(K_kZ_2)\\ &=(1-K_k)^2var(Z_1)+K_k^2var(Z_2)\\ &=(1-K_k)^2\sigma_1^2+K_k^2\sigma_2^2\\ \end{split} σZ^2=var[Z1+Kk(Z2−Z1)]=var(Z1−KkZ1+KkZ2)=var[(1−Kk)Z1+KkZ2]=var[(1−Kk)Z1]+var(KkZ2)=(1−Kk)2var(Z1)+Kk2var(Z2)=(1−Kk)2σ12+Kk2σ22
为了求解方差 v a r ( Z ^ ) var(\hat Z) var(Z^)最小值,对上式进行求导,找其零点,因此易得
δ σ Z ^ 2 δ K k = − 2 ( 1 − K k ) σ 1 2 + 2 K k σ 2 2 = 0 \frac{\delta\sigma_{\hat Z}^2}{\delta K_k} = -2(1-K_k)\sigma_1^2+2K_k\sigma_2^2=0\\ δKkδσZ^2=−2(1−Kk)σ12+2Kkσ22=0
对其进行整理,有
− σ 1 2 + K k σ 1 2 + K k σ 1 2 = 0 K k ( σ 1 2 + σ 2 2 ) = σ 1 2 ⇒ K k = σ 1 2 σ 1 2 + σ 2 2 \begin{split} -\sigma_1^2+K_k\sigma_1^2+K_k\sigma_1^2&=0\\ K_k(\sigma_1^2+\sigma_2^2)&=\sigma_1^2\\ \Rightarrow K_k&=\frac{\sigma_1^2}{\sigma_1^2+\sigma_2^2} \end{split} −σ12+Kkσ12+Kkσ12Kk(σ12+σ22)⇒Kk=0=σ12=σ12+σ22σ12
后验估计表达式的推导
估计真实数据的通常做法为:取多次测量的平均值。根据该思想,写出测量k次时的估计真实值,表达式如下
x ^ k = 1 k ( z 1 + z 2 + . . . + z k ) = 1 k ( z 1 + z 2 + . . . + z k − 1 ) + 1 k z k = 1 k ⋅ k − 1 k − 1 ( z 1 + z 2 + . . . + z k − 1 ) + 1 k z k \begin{split} \hat x_k &= \frac 1k(z_1+z_2+...+z_k)\\ &= \frac 1k(z_1+z_2+...+z_{k-1})+\frac 1kz_k\\ &= \frac 1k·\frac{k-1}{k-1}(z_1+z_2+...+z_{k-1})+\frac 1kz_k\\ \end{split} x^k=k1(z1+z2+...+zk)=k1(z1+z2+...+zk−1)+k1zk=k1⋅k−1k−1(z1+z2+...+zk−1)+k1zk
上式中 ( z 1 + z 2 + . . . + z k − 1 ) / k − 1 (z_1+z_2+...+z_{k-1})/{k-1} (z1+z2+...+zk−1)/k−1为第k-1次测量时的平均估计值 x ^ k − 1 \hat x_{k-1} x^k−1,因此上式可改写为
x ^ k = k − 1 k x ^ k − 1 + 1 k z k = x ^ k − 1 − 1 k x ^ k − 1 + 1 k z k = x ^ k − 1 + 1 k ( z k − x ^ k − 1 ) \begin{split} \hat x_k &= \frac {k-1}{k}\hat x_{k-1}+\frac 1kz_k\\ &= \hat x_{k-1} - \frac 1k \hat x_{k-1} + \frac 1kz_k\\ &= \hat x_{k-1}+\frac 1k(z_k - \hat x_{k-1}) \end{split} x^k=kk−1x^k−1+k1zk=x^k−1−k1x^k−1+k1zk=x^k−1+k1(zk−x^k−1)
式中的 1 k \frac 1k k1称为卡尔曼增益(卡尔曼系数),常写作 K k K_k Kk。经过整理后即为尔曼滤波的核心公式之一,写作
x ^ k = x ^ k − 1 + K k ( z k − x ^ k − 1 ) \hat x_k= \hat x_{k-1}+K_k(z_k - \hat x_{k-1}) x^k=x^k−1+Kk(zk−x^k−1)
该式的物理含义为:
当前的估计值 = 上一次的估计值 + 卡尔曼增益*(当前测量值-上一次的估计值)
误差协方差矩阵的推导
经过上面的推导,现在应用卡尔曼滤波时只剩下联合概率的先验值 P k − P_k^- Pk−是未知的了,因此我们即将推导它的公式,已知联合概率的先验表达式如下
P k − = E ( e k − e k − T ) P_k^- = E(e_k^-e_k^{-T}) Pk−=E(ek−ek−T)
由之前的推导已知
e k − = x k − − x ^ k − = A x k − 1 + B u k − 1 + w k − 1 − A x ^ k − 1 − B u k − 1 = A ( x k − 1 − x ^ k − ) + w k − 1 = A e k − 1 + w k − 1 \begin{split} e_k^- &= x_k^- - \hat x_k^-\\ &= Ax_{k-1} + Bu_{k-1} + w_{k-1} - A \hat x_{k-1} - Bu_{k-1}\\ &= A(x_{k-1} - \hat x_k^-) + w_{k-1}\\ &= Ae_{k-1} + w_{k-1} \end{split} ek−=xk−−x^k−=Axk−1+Buk−1+wk−1−Ax^k−1−Buk−1=A(xk−1−x^k−)+wk−1=Aek−1+wk−1
将该结果代入原式后可得
P k − = E ( e k − e k − T ) = E [ ( A e k − 1 + w k − 1 ) ( A e k − 1 + w k − 1 ) T ] = E [ ( A e k − 1 + w k − 1 ) ( A e k − 1 ) T + ( w k − 1 ) T ] = E [ ( A e k − 1 + w k − 1 ) ( e k − 1 T A T + w k − 1 T ] = E ( A e k − 1 e k − 1 T A T + A e k − 1 w k − 1 T + w k − 1 e k − 1 T A T + w k − 1 w k − 1 T ) = E ( A e k − 1 e k − 1 T A T ) + E ( A e k − 1 w k − 1 T ) + E ( w k − 1 e k − 1 T A T ) + E ( w k − 1 w k − 1 T ) \begin{split} P_k^- &= E(e_k^-e_k^{-T})\\ &= E[(Ae_{k-1} + w_{k-1})(Ae_{k-1} + w_{k-1})^T]\\ &= E[(Ae_{k-1} + w_{k-1})(Ae_{k-1})^T + (w_{k-1})^T]\\ &= E[(Ae_{k-1} + w_{k-1})(e_{k-1}^TA^T + w_{k-1}^T]\\ &= E(Ae_{k-1}e_{k-1}^TA^T + Ae_{k-1}w_{k-1}^T + w_{k-1}e_{k-1}^TA^T + w_{k-1}w_{k-1}^T)\\ &= E(Ae_{k-1}e_{k-1}^TA^T) + E(Ae_{k-1}w_{k-1}^T) + E(w_{k-1}e_{k-1}^TA^T) + E(w_{k-1}w_{k-1}^T)\\ \end{split} Pk−=E(ek−ek−T)=E[(Aek−1+wk−1)(Aek−1+wk−1)T]=E[(Aek−1+wk−1)(Aek−1)T+(wk−1)T]=E[(Aek−1+wk−1)(ek−1TAT+wk−1T]=E(Aek−1ek−1TAT+Aek−1wk−1T+wk−1ek−1TAT+wk−1wk−1T)=E(Aek−1ek−1TAT)+E(Aek−1wk−1T)+E(wk−1ek−1TAT)+E(wk−1wk−1T)
关注上式中的第二项与第三项,根据下式
e k − 1 = x k − 1 − x ^ k − 1 x k = A x k − 1 + B u k − 1 + w k − 1 e_{k-1} = x_{k-1} - \hat x_{k-1}\\ x_k = Ax_{k-1}+Bu_{k-1} + w_{k-1}\\ ek−1=xk−1−x^k−1xk=Axk−1+Buk−1+wk−1
可知, e k − 1 e_{k-1} ek−1作用于k-1时刻,而 w k − 1 w_{k-1} wk−1作用于k时刻,因此两个概率是独立的,并且两者均满足高斯分布,因此它们的期望均为0,因此推导式可写为
P k − = E ( A e k − 1 e k − 1 T A T ) + E ( A e k − 1 ) E ( w k − 1 T ) + A T E ( w k − 1 ) E ( e k − 1 T ) + E ( w k − 1 w k − 1 T ) = E ( A e k − 1 e k − 1 T A T ) + 0 + 0 + E ( w k − 1 w k − 1 T ) = A E ( e k − 1 e k − 1 T ) A T + E ( w k − 1 w k − 1 T ) ⇒ = A P k − 1 A T + Q \begin{split} P_k^- &= E(Ae_{k-1}e_{k-1}^TA^T) + E(Ae_{k-1})E(w_{k-1}^T) + A^TE(w_{k-1})E(e_{k-1}^T) + E(w_{k-1}w_{k-1}^T)\\ &= E(Ae_{k-1}e_{k-1}^TA^T) + 0 + 0 + E(w_{k-1}w_{k-1}^T)\\ &= AE(e_{k-1}e_{k-1}^T)A^T + E(w_{k-1}w_{k-1}^T)\\ \Rightarrow&= AP_{k-1}A^T + Q\\ \end{split} Pk−⇒=E(Aek−1ek−1TAT)+E(Aek−1)E(wk−1T)+ATE(wk−1)E(ek−1T)+E(wk−1wk−1T)=E(Aek−1ek−1TAT)+0+0+E(wk−1wk−1T)=AE(ek−1ek−1T)AT+E(wk−1wk−1T)=APk−1AT+Q
卡尔曼滤波在控制领域应用的推导
控制领域的状态空间方程在实际应用过程中存在着两个问题,其一为表示系统状态的状态量在传输过程中存在着过程噪声 w w w,以及基于传感器等的测量的实际输出量存在着测量噪声 v v v。由于这两个未知量的引入,导致我们实际得到的数据与真实值存在一个波动的误差。带噪声的状态空间方程表示如下
{ x k = A x k − 1 + B u k − 1 + w k − 1 z k = H x k + v k \begin{cases} x_k = Ax_{k-1}+Bu_{k-1}+w_{k-1}\\ z_k = Hx_k + v_k \end{cases} {xk=Axk−1+Buk−1+wk−1zk=Hxk+vk
噪声的取值满足高斯分布,分别写作 P ( w ) ∼ N ( 0 , Q ) P(w)\sim N(0,Q) P(w)∼N(0,Q)以及 P ( w ) ∼ N ( 0 , R ) P(w)\sim N(0,R) P(w)∼N(0,R)。由于这两个噪声的存在,状态量与输出量就从原来的真实值变成了带偏差的估计值。根据原有的状态空间方程我们可以得到状态量的先验估计值(算出来的结果) x ^ k − \hat x_k^- x^k−以及测量估计值(测出来的结果) x ^ k m e a s \hat x_{k_{meas}} x^kmeas,他们的计算公式如下
{ x k = A x k − 1 + B u k − 1 z k = H x k ⇒ { x ^ k − = A x k − 1 + B u k − 1 x ^ k m e a s = H − 1 z k \begin{cases} x_k = Ax_{k-1}+Bu_{k-1}\\ z_k = Hx_k \end{cases}\\ \Rightarrow \begin{cases} \hat x_k^- = Ax_{k-1}+Bu_{k-1}\\ \hat x_{k_{meas}} = H^{-1}z_k \end{cases} {xk=Axk−1+Buk−1zk=Hxk⇒{x^k−=Axk−1+Buk−1x^kmeas=H−1zk
由于误差是无法通过建模得到的,因此只能引入概率论中的相关知识,由这两个带误差的结果得到一个更加接近真实值的结果(上节的推导)。根据之前的推导,它们之间存在如下关系
x ^ k = x ^ k − + G ( H − 1 z k − x ^ k − ) \hat x_k = \hat x_k^- + G(H^{-1}z_k - \hat x_k^-) x^k=x^k−+G(H−1zk−x^k−)
这种经过处理得到的更为接近的对真值的估计值被称作后验估计 x ^ k \hat x_k x^k。为了方便理解,上式通常会进行该变换 G = K k H G=K_kH G=KkH,经该变换后 K k K_k Kk的取值由原来的 [ 0 , 1 ] [0,1] [0,1]变为 [ 0 , H − 1 ] [0,H^{-1}] [0,H−1]。上式经整理后写作
x ^ k = x ^ k − + K k ( z k − H x ^ k − ) \hat x_k = \hat x_k^- + K_k(z_k - H\hat x_k^-) x^k=x^k−+Kk(zk−Hx^k−)
此时我们的目标就变为了:寻找一个 K k K_k Kk使得 x ^ k ⇒ x k \hat x_k \Rightarrow x_k x^k⇒xk,在概率论中表示即为 t r ( p ) tr(p) tr(p)最小。写作
e k = x k − x ^ k = x k − [ x ^ k − + K k ( z k − H x ^ k − ) ] = x k − x ^ k − − K k z k + K k H x ^ k − = x k − x ^ k − − K k ( H x k + v k ) + K k H x ^ k − = x k − x ^ k − − K k H x k − K k v k + K k H x ^ k − = ( x k − x ^ k − ) − K k H ( x k − x ^ k − ) − K k v k = ( I − K k H ) ( x k − x ^ k − ) − K k v k \begin{split} e_k &= x_k - \hat x_k\\ &= x_k -[\hat x_k^- + K_k(z_k - H\hat x_k^-)]\\ &= x_k -\hat x_k^- - K_kz_k + K_kH\hat x_k^-\\ &= x_k -\hat x_k^- - K_k(Hx_k + v_k) + K_kH\hat x_k^-\\ &= x_k -\hat x_k^- - K_kHx_k - K_kv_k + K_kH\hat x_k^-\\ &= (x_k -\hat x_k^-) - K_kH(x_k - \hat x_k^-) - K_kv_k \\ &= (I-K_kH)(x_k -\hat x_k^-) - K_kv_k \\ \end{split} ek=xk−x^k=xk−[x^k−+Kk(zk−Hx^k−)]=xk−x^k−−Kkzk+KkHx^k−=xk−x^k−−Kk(Hxk+vk)+KkHx^k−=xk−x^k−−KkHxk−Kkvk+KkHx^k−=(xk−x^k−)−KkH(xk−x^k−)−Kkvk=(I−KkH)(xk−x^k−)−Kkvk
其中, x k − x ^ k − x_k -\hat x_k^- xk−x^k−可以写作误差的先验值 e k − e_k^- ek−。假设误差 e k e_k ek满足高斯分布,即 p ( e k ) ∼ N ( 0 ( 期望 ) , P ( 方差 ) ) p(e_k)\sim N(0(期望),P(方差)) p(ek)∼N(0(期望),P(方差)),其方差可表示为
P k = E [ e k e k T ] = E [ ( x k − x ^ k ) ( x k − x ^ k ) T ] = E { [ ( I − K k H ) e k − − K k v k ] [ ( I − K k H ) e k − − K k v k ] T } = E { [ ( I − K k H ) e k − − K k v k ] [ e k − T ( I − K k H ) T − v k T K k T } = E { [ ( I − K k H ) e k − − K k v k ] [ e k − T ( I − K k H ) T − v k T K k T } = E [ ( I − K k H ) e k − e k − T ( I − K k H ) T − ( I − K k H ) e k − v k T K k T − v k K k e k − T ( I − K k H ) T + v k K k v k T K k T ] = E [ ( I − K k H ) e k − e k − T ( I − K k H ) T ] − E [ ( I − K k H ) e k − v k T K k T ] − E [ v k K k e k − T ( I − K k H ) T ] + E [ v k K k v k T K k T ] \begin{split} P_k &= E[e_ke_k^T]\\ &=E[(x_k -\hat x_k)(x_k -\hat x_k)^T]\\ &=E \lbrace [(I-K_kH)e_k^- - K_kv_k][(I-K_kH)e_k^- - K_kv_k]^T \rbrace\\ &=E \lbrace [(I-K_kH)e_k^- - K_kv_k] [e_k^{-T}(I-K_kH)^T - v_k^TK_k^T \rbrace\\ &=E \lbrace [(I-K_kH)e_k^- - K_kv_k] [e_k^{-T}(I-K_kH)^T - v_k^TK_k^T \rbrace\\ &=E [ (I-K_kH)e_k^-e_k^{-T}(I-K_kH)^T - (I-K_kH)e_k^-v_k^TK_k^T - v_kK_ke_k^{-T}(I-K_kH)^T + v_kK_kv_k^TK_k^T ]\\ &=E[(I-K_kH)e_k^-e_k^{-T}(I-K_kH)^T] - E[(I-K_kH)e_k^-v_k^TK_k^T] - E[v_kK_ke_k^{-T}(I-K_kH)^T] + E[v_kK_kv_k^TK_k^T]\\ \end{split} Pk=E[ekekT]=E[(xk−x^k)(xk−x^k)T]=E{[(I−KkH)ek−−Kkvk][(I−KkH)ek−−Kkvk]T}=E{[(I−KkH)ek−−Kkvk][ek−T(I−KkH)T−vkTKkT}=E{[(I−KkH)ek−−Kkvk][ek−T(I−KkH)T−vkTKkT}=E[(I−KkH)ek−ek−T(I−KkH)T−(I−KkH)ek−vkTKkT−vkKkek−T(I−KkH)T+vkKkvkTKkT]=E[(I−KkH)ek−ek−T(I−KkH)T]−E[(I−KkH)ek−vkTKkT]−E[vkKkek−T(I−KkH)T]+E[vkKkvkTKkT]
其中 ( I − K k H ) (I-K_kH) (I−KkH)和 K k T K_k^T KkT都是常数,可以直接从期望计算中提取出来。第二项和第三项其实是等价的,进一步写为
2 ( I − K k H ) K k T ⋅ E ( e k − v k T ) 2(I-K_kH)K_k^T·E(e_k^-v_k^T) 2(I−KkH)KkT⋅E(ek−vkT)
由于先验误差和测量误差是相互独立的,因此上式改写为
2 ( I − K k H ) K k T ⋅ E ( e k − ) E ( v k T ) 2(I-K_kH)K_k^T·E(e_k^-)E(v_k^T) 2(I−KkH)KkT⋅E(ek−)E(vkT)
而二者都满足高斯分布,因此它们各自的期望值均为0,该项的结果为0。则原式子写为
P k = ( I − K k H ) E ( e k − e k − T ) ( I − K k H ) T − E [ ( I − K k H ) e k − v k T K k T ] + K k E ( v k v k T ) K k T = ( P k − − K k H P k − ) ( I − H T K k T ) + K k R K k T ⇒ = P k − − P k − H T K k T − K k H P k − + K k H P k − H T K k T + K k R K k T \begin{split} P_k &= (I-K_kH)E(e_k^-e_k^{-T})(I-K_kH)^T - E[(I-K_kH)e_k^-v_k^TK_k^T] + K_kE(v_kv_k^T)K_k^T\\ &= (P_k^- - K_kHP_k^-)(I - H^TK_k^T) + K_kRK_k^T\\ \Rightarrow&= P_k^- - P_k^-H^TK_k^T - K_kHP_k^- + K_kHP_k^-H^TK_k^T + K_kRK_k^T \end{split} Pk⇒=(I−KkH)E(ek−ek−T)(I−KkH)T−E[(I−KkH)ek−vkTKkT]+KkE(vkvkT)KkT=(Pk−−KkHPk−)(I−HTKkT)+KkRKkT=Pk−−Pk−HTKkT−KkHPk−+KkHPk−HTKkT+KkRKkT
t r ( A B ) tr(AB) tr(AB)为矩阵A与矩阵B相乘后对角线元素之和,改写为求解 P k P_k Pk的迹的形式为
t r ( P k ) = t r ( P k − ) − 2 t r ( K k H P k − ) + t r ( K k H P k − H T K k T ) + t r ( K k R K k T ) tr(P_k) = tr(P_k^-) - 2tr(K_kHP_k^-) + tr(K_kHP_k^-H^TK_k^T) + tr(K_kRK_k^T) tr(Pk)=tr(Pk−)−2tr(KkHPk−)+tr(KkHPk−HTKkT)+tr(KkRKkT)
为了求解迹最小的情况,以下表述出其一阶导数形式
d t r ( P k ) d K k = 0 − 2 ( H P k − ) T + 2 K k H P k − H T + 2 K k R = P k − T H T + K k ( H P k − H T + R ) (协方差矩阵的转置等于它自己) = P k − T H + K k ( H P k − H T + R ) \begin{split} \frac{dtr(P_k)}{dK_k} &= 0 - 2(HP_k^-)^T + 2K_kHP_k^-H^T + 2K_kR\\ &= P_k^{-T}H^T + K_k(HP_k^-H^T + R)\\ (协方差矩阵的转置等于它自己)&= P_k^{-T}H + K_k(HP_k^-H^T + R)\\ \end{split} dKkdtr(Pk)(协方差矩阵的转置等于它自己)=0−2(HPk−)T+2KkHPk−HT+2KkR=Pk−THT+Kk(HPk−HT+R)=Pk−TH+Kk(HPk−HT+R)
上式求解中涉及到一个矩阵求偏导的变换,写作
d t r ( A B ) d A = B T \frac{dtr(AB)}{dA} = B^T dAdtr(AB)=BT
其证明如下
t r ( A B ) = A ⋅ B = [ a 11 a 12 a 21 a 22 ] [ b 11 b 12 b 21 b 22 ] 取对角元素之和 = a 11 b 11 + a 12 b 21 + a 21 b 12 + a 22 b 22 d t r ( A B ) d A = [ ∂ t r ( A B ) ∂ a 11 ∂ t r ( A B ) ∂ a 12 ∂ t r ( A B ) ∂ a 21 ∂ t r ( A B ) ∂ a 22 ] = [ b 11 b 12 b 21 b 22 ] = B T \begin{split} tr(AB) &= A·B \\ &= \begin{bmatrix} a_{11}&a_{12}\\a_{21}&a_{22} \end{bmatrix} \begin{bmatrix} b_{11}&b_{12}\\b_{21}&b_{22} \end{bmatrix}\\ 取对角元素之和&= a_{11}b_{11} + a_{12}b_{21} + a_{21}b_{12} + a_{22}b_{22}\\ \frac{dtr(AB)}{dA} &= \begin{bmatrix} \frac{\partial tr(AB)}{\partial a_{11}}& \frac{\partial tr(AB)}{\partial a_{12}}\\ \frac{\partial tr(AB)}{\partial a_{21}}& \frac{\partial tr(AB)}{\partial a_{22}}\\ \end{bmatrix}\\ &= \begin{bmatrix} b_{11}&b_{12}\\ b_{21}&b_{22}\\ \end{bmatrix}\\ &= B^T \end{split} tr(AB)取对角元素之和dAdtr(AB)=A⋅B=[a11a21a12a22][b11b21b12b22]=a11b11+a12b21+a21b12+a22b22=[∂a11∂tr(AB)∂a21∂tr(AB)∂a12∂tr(AB)∂a22∂tr(AB)]=[b11b21b12b22]=BT
当一阶导为零时,此时求得的值为迹的最小(最优解),整理如下
d t r ( P k ) d K k = P k − T H + K k ( H P k − H T + R ) = 0 ⇒ 0 − 2 ( h P k − ) T + 2 K k H P k − H T + 2 K k R = 0 − P k − H T + K k ( H P k − + R ) = 0 K k ( H P k − H T + R ) = P k − H T ⇒ K k = P k − H T H P k − H T + R \frac{dtr(P_k)}{dK_k} = P_k^{-T}H + K_k(HP_k^-H^T + R) = 0\\ \begin{split} \Rightarrow 0 - 2(hP_k^-)^T + 2K_kHP_k^-H^T + 2K_kR &= 0\\ -P_k^-H^T + K_k(HP_k^-+R) &= 0\\ K_k(HP_k^-H^T + R) &= P_k^-H^T\\ \Rightarrow K_k = \frac{P_k^-H^T}{HP_k^-H^T + R} \end{split} dKkdtr(Pk)=Pk−TH+Kk(HPk−HT+R)=0⇒0−2(hPk−)T+2KkHPk−HT+2KkR−Pk−HT+Kk(HPk−+R)Kk(HPk−HT+R)⇒Kk=HPk−HT+RPk−HT=0=0=Pk−HT
卡尔曼增益详解
卡尔曼增益的计算方式
估计误差 ( e s t i m a t e ) e E S T = ∣ x − x ^ ∣ 测量误差 ( m e a s u r e ) e M E A = ∣ x − z ∣ 卡尔曼增益 K k = e E S T k − 1 e E S T k − 1 + e M E A k 估计误差(estimate)\hspace{0.5cm}e_{EST} = |x - \hat x|\\ 测量误差(measure)\hspace{0.5cm}e_{MEA} = |x - z|\\ 卡尔曼增益\hspace{0.5cm}K_k = \frac{e_{EST_{k-1}}}{e_{EST_{k-1}}+e_{MEA_k} } 估计误差(estimate)eEST=∣x−x^∣测量误差(measure)eMEA=∣x−z∣卡尔曼增益Kk=eESTk−1+eMEAkeESTk−1
卡尔曼增益的解读
在k时刻,存在两种情况
① k-1时刻的估计误差远远大于k时的测量误差,即
e E S T k − 1 ≫ e M E A k e_{EST_{k-1}} \gg e_{MEA_k} eESTk−1≫eMEAk
有以下关系
{ K k ⇒ 1 x ^ k = x ^ k − 1 + z k − x ^ k − 1 = z k \begin{cases} \begin{split} K_k&\Rightarrow1\\ \hat x_k &= \hat x_{k-1} + z_k - \hat x_{k-1} \\ &= z_k \end{split} \end{cases} ⎩ ⎨ ⎧Kkx^k⇒1=x^k−1+zk−x^k−1=zk
此时第k次的估计真值等于第k次的测量值
② k-1时刻的估计误差远远小于k时的测量误差
e E S T k − 1 ≪ e M E A k e_{EST_{k-1}} \ll e_{MEA_k} eESTk−1≪eMEAk
有以下关系
{ K k ⇒ 0 x ^ k = x ^ k − 1 \begin{cases} K_k\Rightarrow0\\ \hat x_k = \hat x_{k-1} \end{cases} {Kk⇒0x^k=x^k−1
此时第k次的估计真值等于上一次的估计真值。
卡尔曼滤波的应用
普通应用中的一般流程
- 计算卡尔曼增益 K k K_k Kk
K k = e E S T k − 1 e E S T k − 1 + e M E A k K_k = \frac{e_{EST_{k-1}}}{e_{EST_{k-1}}+e_{MEA_k}} Kk=eESTk−1+eMEAkeESTk−1 - 计算当前的估计值 x ^ k \hat x_k x^k
x ^ k = x ^ k − 1 + K k ⋅ ( z k − x ^ k − 1 ) \hat x_k= \hat x_{k-1}+K_k·(z_k - \hat x_{k-1}) x^k=x^k−1+Kk⋅(zk−x^k−1) - 更新当前的估计误差 e E S T k e_{EST_k} eESTk
e E S T k = ( 1 − K k ) ⋅ e E S T k − 1 e_{EST_k} = (1-K_k)·e_{EST_{k-1}} eESTk=(1−Kk)⋅eESTk−1
实例说明
生产硬币的机器在实际生产时会由于各种影响因素导致误差生产出来的硬币直径与设计尺寸存在一定误差(误差1),当我们对真实硬币的直径进行测量时,每次也会引入一定误差(误差2)。利用卡尔曼滤波对硬币真实的直径进行预测。
应用实例(matlab):预测实际硬币的直径
clear;clc;close all;
%% 测量硬币的直径,已知条件
x = 50; % 实际长度,mm
hat_x = 45; % 第一次估计值
est_error = 5; % 估计误差
z = [51 48 47 52 51 48 49 53 48 49 52 53 51 52 49 50]; % 测量长度
mea_error = 3; % 测量误差,即测量值在真实值±3mm内波动
%% main
k = 16;
K_k = zeros(k,1);
for i = 1:kK_k(i) = est_error/(est_error + mea_error); % Kalman_Gainhat_x = hat_x + K_k(i)*(z(i)-hat_x);Hat_x(i) = hat_x;est_error = (1-K_k(i))*est_error;Est_error(i) = est_error;
end
figure;
plot(ones(1,17)*x,'g-');hold on;
plot(z,'ro-');hold on;
plot([45,Hat_x],'bo-')
legend("真实值","测量值","滤波后的估计值",'Location','southeast')
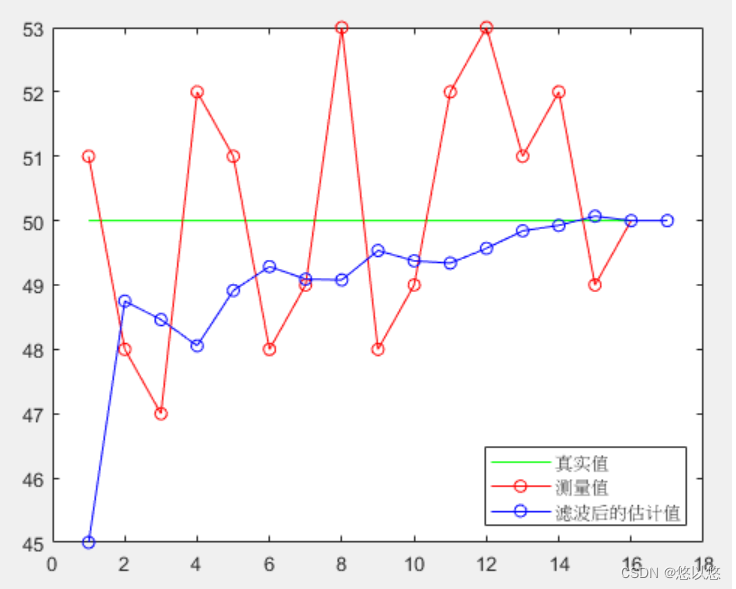
这篇关于卡尔曼滤波(Kalman Filter,KF)基础推导及其实例的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






