27[NLP训练营]collapsed gibbs sampling

回顾

下图是LDA生成的过程。

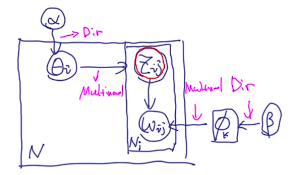
为了更好描述collapsed gibbs sampling。把里面的标识换一下，问题的描述变成：
计算$P(Z_{ts}|Z_{-ts},w,\alpha ,\beta )$
$t$代表第$t$个文档
$s$代表第$t$个文档的第$s$个单词

假设有一个集合
x = { x 1 , x 2 , . . . x n } x=\{x_1,x_2,...x_n\} x={x1​,x2​,...xn​}
那么它可以表示为：
$x=x_i\cup x_{-i}$
同样的，问题描述中的$Z=Z_{ts}\cup Z_{-ts}$

第一步

可以看到，问题描述中是没有$\varphi ,\theta$的，我们就是要用collapsed 的方式把这两个变量进行边缘化，
$$P(Z_{ts}|Z_{-ts},w,\alpha ,\beta )=\frac{P(Z,w|\alpha ,\beta )}{P(Z_{-ts},w|\alpha ,\beta )}$$
变成这个形式是有点原因的，$w$是观测到的结果，把它挪到概率的前面部分，就相对于利用观测值来推断参数，可以走likelihood的套路。

上面的式子为什么会相等呢？
$$\begin{array}{rl}& \frac{P(Z,w|\alpha ,\beta )}{P(Z_{-ts},w|\alpha ,\beta )}\ast \frac{P(\alpha ,\beta )}{P(\alpha ,\beta )}\\ & =\frac{P(Z,w,\alpha ,\beta )}{P(Z_{-ts},w,\alpha ,\beta )}\end{array}\text{\hspace{1em}(1)}$$
$$\begin{array}{rl}& P(Z_{ts}|Z_{-ts},w,\alpha ,\beta )\times P(Z_{-ts},w,\alpha ,\beta )\\ & =P(Z_{ts},Z_{-ts},w,\alpha ,\beta )\\ & =P(Z,w,\alpha ,\beta )\end{array}\text{\hspace{1em}(2)}$$
把公式2代入1就得到上面的等式了。

第二步 看分子

把第一步中的分子分母分开看，先看分子
$$P(Z,w|\alpha ,\beta )$$
如果要把$\varphi ,\theta$边缘化就是要写成下面的积分：
$$\begin{array}{rl}P(Z,w|\alpha ,\beta )& =P(Z|\alpha )\cdot P(w|Z,\beta )\\ & =\int P(Z|\theta )\cdot P(\theta |\alpha )d\theta \int P(w|Z,\varphi )\cdot P(\varphi |\beta )d\varphi \end{array}$$
上面第一个等号实际上是根据LDA那个图进行拆分了一下，用依赖关系把联合概率拆分成对应的条件概率。上面的联合概率是有条件的，就是已知的超参数$\alpha ,\beta$

按上面的图本来第一个等号后面应该是写：$P(Z|\theta )\cdot P(w|Z,\varphi )$，但是为了要把$\theta ,\varphi$进行边缘化，我们就把这个路径直接取到$\alpha ,\beta$那里了。

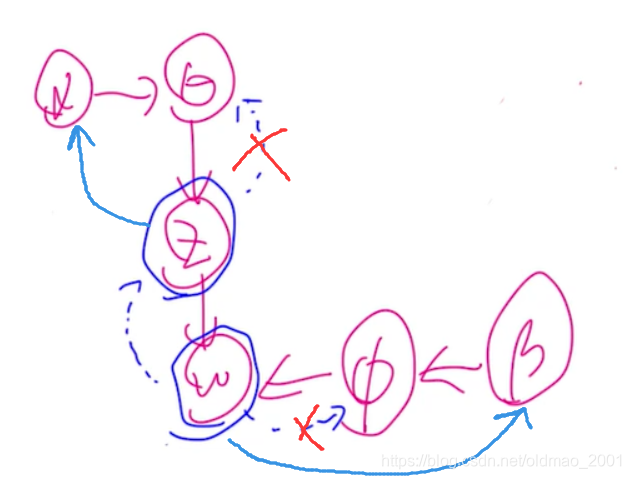
所以就写成了：$P(Z|\alpha )\cdot P(w|Z,\beta )$

分别看上面的两项积分：

第一项

第一项中$P(Z|\theta )$相当于multinomial分布，$P(\theta |\alpha )$相当于狄利克雷分布，因此根据分布的性质可以展开（上面用ts来代表新下标，这里又回到原来的ij了。。。）：
$$\begin{array}{rl}& \int P(Z|\theta )\cdot P(\theta |\alpha )d\theta \\ & =\int \prod _{i=1}^N\prod _{j=1}^{N_i}\prod _{k=1}^K{\theta }_{ik}^{I(Z_{ij}=k)}\cdot \prod _{i=1}^N\frac{1}{\mathrm{B}(\alpha )}\prod _{k=1}^K{\theta }_{ik}^{{\alpha }_k-1}d{\theta }_k\\ & =\prod _{i=1}^N\int \prod _{j=1}^{N_i}\prod _{k=1}^K{\theta }_{ik}^{I(Z_{ij}=k)}\cdot \frac{1}{\mathrm{B}(\alpha )}\prod _{k=1}^K{\theta }_{ik}^{{\alpha }_k-1}d{\theta }_k\end{array}$$
先解释一下第一个等号的第一项：${\prod }_{i=1}^N{\prod }_{j=1}^{N_i}$表示两层循环，每个文章，每个文章中的单词，第三个虽然是连乘，但是由于indicator函数的存在，每次只会有一个${\theta }_{ik}$出现。
第二项是把所有文档的主题分布拆分单个文档主题分布的累加，所以第一个${\prod }_{i=1}^N$表示所有文章的狄利克雷分布的累加。

这里把连乘${\prod }_{j=1}^{N_i}$放到指数变成累加${\sum }_{j=1}^{N_i}$，然后和后面的${\theta }_{ik}^{{\alpha }_k-1}$的指数进行相加，上式变为：
$$=\prod _{i=1}^N\frac{1}{\mathrm{B}(\alpha )}\int \prod _{k=1}^K{\theta }_{ik}^{{\sum }_{j=1}^{N_i}I(Z_{ij}=k)+{\alpha }_k-1}d{\theta }_k\text{\hspace{1em}(3)}$$
根据狄利克雷分布的概念：
$$Dir(\theta |\alpha )=\frac{1}{\mathrm{B}(\alpha )}\prod _{k=1}^K{\theta }_{ik}^{{\alpha }_k-1}$$
可以看到公式3积分那个部分其实可以凑成狄利克雷分布，最后变成：
$$(3)=\prod _{i=1}^N\frac{\mathrm{B}(\alpha +{\sum }_{j=1}^{N_i}{I}_k(Z_{ij}))}{\mathrm{B}(\alpha )}\text{\hspace{1em}(4)}$$
这里给个例子看看${\sum }_{j=1}^{N_i}{I}_k(Z_{ij})$是怎么算（i是文章编号，j是第i篇文章中的单词编号），例如一个文档里面有六个词，每个词对应的主题$Z_{ij}$如下

也就是主题为1的有2个词，为2的有3个词，为3的有1个词，因此${\sum }_{j=1}^{N_i}{I}_k(Z_{ij})=(2,3,1)$
公式4中$\alpha$通常是一个向量，可以写作：$({\alpha }_1,{\alpha }_2,{\alpha }_3,...)$
因此， 公式4中的分子就变成了$\mathrm{B}({\alpha }_1+2,{\alpha }_2+3,{\alpha }_3+1)$，分母变成了$\mathrm{B}({\alpha }_1,{\alpha }_2,{\alpha }_3)$
通俗理解就是有一个初始的$\alpha$，然后根据主题词的个数对$\alpha$进行调整，这里其实和上面的吉布斯采样中的${\theta }_i$的采样结果一样样的。

第二项

$$\int P(w|Z,\varphi )\cdot P(\varphi |\beta )d\varphi$$
跟第一项类似的，是一个multinomial和dirichlet分布相乘，经过上面的证明我们知道这两个东西相乘结果还是一个dirichlet分布。上式：
$$=\int \prod _{k=1}^K\prod _{i:Z_i=k}\prod _{v=1}^V{\varphi }_{k,v}^{I(w_i=v)}\cdot \prod _{k=1}^K\frac{1}{\mathrm{B}(\beta )}\prod _{v=1}^V{\varphi }_{k,v}^{{\beta }_v-1}d{\varphi }_k$$
$P(\varphi |\beta )$对应上面的第二项，第二项的第一个连乘${\prod }_{k=1}^K$意思是$P(\varphi |\beta )$有K个主题，每个主题都是从狄利克雷分布采样得来的。第二个连乘代表这个主题下的单词，由于考虑所有单词的情况，因此其单词数量记为$V$。
为了和第一项一样的思路，这里要把$P(w|Z,\varphi )$也要凑出来主题和所有单词的嵌套连乘，那么就从主题的角度来考虑，每个单词必定是属于某个主题的，因此先循环所有主题：${\prod }_{k=1}^K$
这里的$i:Z_i=k$意思是所有的单词i是属于主题k的（相当于，从所有单词里面把满足$Z_i=k$这个条件的单词i，取出来），另外也可以把连乘变成指数上的累加：
$$\begin{array}{rl}& =\prod _{k=1}^K\frac{1}{\mathrm{B}(\beta )}\int \prod _{v=1}^V{\varphi }_{k,v}^{{\sum }_{i:Z_i=k}I(w_i=v)+{\beta }_v-1}d{\varphi }_k\\ & =\prod _{k=1}^K\frac{\mathrm{B}(\beta +{\sum }_{i:Z_i=k}{I}_v(w_i))}{\mathrm{B}(\beta )}\end{array}$$

联合第一、第二项

$$\begin{array}{rl}P(Z,w|\alpha ,\beta )& =第一项\cdot 第二项\\ & =\prod _{i=1}^N\frac{\mathrm{B}(\alpha +{\sum }_{j=1}^{N_i}{I}_k(Z_{ij}))}{\mathrm{B}(\alpha )}\cdot \prod _{k=1}^K\frac{\mathrm{B}(\beta +{\sum }_{i:Z_i=k}{I}_v(w_i))}{\mathrm{B}(\beta )}\end{array}$$

第二步 看分母

$$P(Z_{-ts},w|\alpha ,\beta )$$
也就是不考虑$Z_{ts}$
$$\begin{array}{rl}& P(Z_{-ts},w|\alpha ,\beta )\\ & =\prod _{i=1}^N\frac{\mathrm{B}(\alpha +{\sum }_{j=1,{\delta }_j\ne (t,s)}^{N_i}{I}_k(Z_{ij}))}{\mathrm{B}(\alpha )}\cdot \prod _{k=1}^K\frac{\mathrm{B}(\beta +{\sum }_{i:Z_i=k,{\delta }_j\ne (t,s)}{I}_v(w_i))}{\mathrm{B}(\beta )}\end{array}$$
${\delta }_j$代表当前单词所在的位置

分子分母同时看

$$P(Z_{ts}|Z_{-ts},w,\alpha ,\beta )=\frac{分子}{分母}$$
可以看到分子和分母除了第t个文档，其他项是一样的，由于最外面是连乘，所以可以都消掉（这里的下标又把i换成了t，有点乱。。。）：
$$P(Z_{ts}|Z_{-ts},w,\alpha ,\beta )=\frac{\mathrm{B}(\alpha +{\sum }_{j=1}^{N_t}{I}_k(Z_{tj}))}{\mathrm{B}(\alpha +{\sum }_{j=1,j\ne s}^{N_t}{I}_k(Z_{tj}))}\frac{\mathrm{B}(\beta +{\sum }_{i:Z_i=k}{I}_v(w_i))}{\mathrm{B}(\beta +{\sum }_{i:Z_i=k,{\delta }_j\ne (t,s)}{I}_v(w_i))}$$
下面就是利用$\mathrm{B}$函数来进行简化。

化简

用例子来看上面的
$$\frac{\mathrm{B}(\alpha +{\sum }_{j=1}^{N_i}{I}_k(Z_{ij}))}{\mathrm{B}(\alpha +{\sum }_{j=1,j\ne s}^{N_i}{I}_k(Z_{ij}))}$$
的分子和分母
先看分子${\sum }_{j=1}^{N_i}{I}_k(Z_{ij})$是怎么算，这个在上节有讲过，这里再详细写下，例如一个文档里面有六个词，每个词对应的主题$Z_{ij}$如下

也就是主题为1的有3个词，为2的有2个词，为3的有1个词，因此${\sum }_{j=1}^{N_i}{I}_k(Z_{ij})=(3,2,1)$
上式中$\alpha$通常是一个向量，可以写作：$({\alpha }_1,{\alpha }_2,{\alpha }_3,...,{\alpha }_k)$
因此上式的分子就变成了$\mathrm{B}({\alpha }_1+3,{\alpha }_2+2,{\alpha }_3+1)$。
由于分母不包含当前词的主题，当当前词是$w_{i1}$的时候，分母变成了$\mathrm{B}({\alpha }_1+2,{\alpha }_2+2,{\alpha }_3+1)$
因此：
$$\frac{\mathrm{B}(\alpha +{\sum }_{j=1}^{N_i}{I}_k(Z_{ij}))}{\mathrm{B}(\alpha +{\sum }_{j=1,j\ne s}^{N_i}{I}_k(Z_{ij}))}=\frac{\mathrm{B}({\alpha }_1+n_{t1},{\alpha }_2+n_{t2}+...+{\alpha }_k+n_{kt1})}{\mathrm{B}({\alpha }_1+n_{t1}^{\prime },{\alpha }_2+n_{t2}^{\prime }+...+{\alpha }_k+n_{kt1}^{\prime })}\text{\hspace{1em}(5)}$$
$n_{ti}$表示第$t$个文档有多少单词被分配主题$i$
$n_{ti}^{\prime }$表示去掉$Z_{ts}$后，第$t$个文档有多少单词被分配主题$i$
这里的分子分母都有$k$项，而且只有一项不一样。
继续化简前先给出$\mathrm{B}$函数的形式：

因此：$$\mathrm{B}({\alpha }_1,{\alpha }_2,{\alpha }_3,...,{\alpha }_k)=\frac{{\prod }_{k=1}^K(\Gamma ({\alpha }_k)}{\Gamma ({\sum }_{k=1}^K{\alpha }_k)}$$
$$(5)=\frac{{\prod }_{k=1}^K(\Gamma ({\alpha }_k+n_{tk}))}{\Gamma ({\sum }_{k=1}^K({\alpha }_k+n_{tk}))}\cdot \frac{\Gamma ({\sum }_{k=1}^K({\alpha }_k+n_{tk}^{\prime }))}{{\prod }_{k=1}^K(\Gamma ({\alpha }_k+n_{tk}^{\prime }))}$$
伽玛函数：$\Gamma (n)=(n-1)!$，而且上面提到过${\alpha }_k+n_{tk}$和${\alpha }_k+n_{tk}^{\prime }$都有k项，而且只有一项不一样，且不一样的项相差1。例如：
当$Z_{ts}=2$，则$n_{t2}-n_{t2}^{\prime }=1$且$n_{ti}=n_{ti}^{\prime },i\ne 2$，因此：
$$\begin{gathered} (5)=\frac{{\prod }_{k=1}^K(\Gamma ({\alpha }_k+n_{tk}))}{{\prod }_{k=1}^K(\Gamma ({\alpha }_k+n_{tk}^{\prime }))}\cdot \frac{\Gamma ({\sum }_{k=1}^K({\alpha }_k+n_{tk}^{\prime }))}{\Gamma ({\sum }_{k=1}^K({\alpha }_k+n_{tk}))} \\ =\frac{{\alpha }_k+n_{tu}^{new}}{{\sum }_{k=1}^K{\alpha }_k+n_t^{new}}\cdot \frac{{\beta }_{w_i}+n_{u{w}_i}^{new}}{{\sum }_{v=1}^V{\beta }_v+n_u^{new}} \end{gathered}$$
$n_{tu}^{new}$表示当前第t个文档有多少个单词被分配到主题u（丢掉$Z_{ts}$，不考虑当前词）
$n_t^{new}$表示当前第t个文档的单词数量（丢掉$Z_{ts}$，不考虑当前词）
$n_{u{w}_i}^{new}$表示对于单词$w_i$有多少次被分配到了主题u（丢掉$Z_{ts}$，不考虑当前词）
$n_u^{new}$表示所有文档中有多少单词分配到了主题u（丢掉$Z_{ts}$，不考虑当前词）

小栗子

假设有两个文档：

主题数量k为3，词库大小为4.
先随机初始化每个单词的主题。

超参数$\alpha =(0.1,0.1,0.1),\beta =(0.1,0.1,0.1,0.1)$
下面按化简后的公式来进行计算第一个文档的第一个单词：

这个时候把第一个单词【今天】从文档1中去掉，可以看到$n_{1,1}^{new}=2$（就是还有2个单词分配到主题1），$n_1^{new}=6$（还剩下6个单词）
因为每一个单词在不同文档可以有不同的主题，也就是有不同的主题概率分布，因此：把第一个单词【今天】从文档1中去掉，没有【今天】分配到主题1，因此$n_{1,w_1}^{new}=0$，但是除了第一个单词【今天】外，分配到主题1的单词有3个，因此$n_1^{new}=3$
$$P(Z_{1,1}=1|Z_{-(1,1)},w,\alpha ,\beta )=\frac{0.1+2}{0.1+0.1+0.1+6}\cdot \frac{0.1+0}{0.1+0.1+0.1+0.1+3}$$
同理：
$$P(Z_{1,1}=2|Z_{-(1,1)},w,\alpha ,\beta )=\frac{0.1+2}{0.1+0.1+0.1+6}\cdot \frac{0.1+1}{0.1+0.1+0.1+0.1+5}$$
$$P(Z_{1,1}=3|Z_{-(1,1)},w,\alpha ,\beta )=\frac{0.1+2}{0.1+0.1+0.1+6}\cdot \frac{0.1+2}{0.1+0.1+0.1+0.1+4}$$
计算完毕后，进行归一化得到（使得累加等于1）：

然后就可以进行multinomial采样。

小结

$$P(Z_{ts}|Z_{-ts},w,\alpha ,\beta )=\frac{{\alpha }_k+n_{tu}^{new}}{{\sum }_{k=1}^K{\alpha }_k+n_t^{new}}\cdot \frac{{\beta }_{w_i}+n_{u{w}_i}^{new}}{{\sum }_{v=1}^V{\beta }_v+n_u^{new}}$$
右边的第一项代表一个文档中的单词的主题分类，当一个文档中的单词分类越集中，主题也越集中，例如一个文档中的有10个单词，前面9个都是主题1，那么第十个单词也会倾向于采样为第1个主题。
第二项是所有文档中某个单词的主题分类影响，例如所有文章中某个单词出现100次，80次是主题1，那么该单词被抽样为主题1的概率越大。