本文主要是介绍OpenSSL密码库算法笔记——第5.4.1章 椭圆曲线上点的仿射坐标表示,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
椭圆曲线上点的表示分成仿射坐标系表示和射影坐标表示形式,首先来看看仿射坐标表示形式。
素域Fp上的椭圆曲线E由(仿射)方程y2=x3+ax+b决定,设曲线上的两个点为P1=(x1,y1),P2=(x2,y2),并且记椭圆曲线加法群的单位元为,称为无穷远点或者零点。如果P1≠-P2,则P3=P1+P2=(x3,y3),可以由如下公式计算出来:
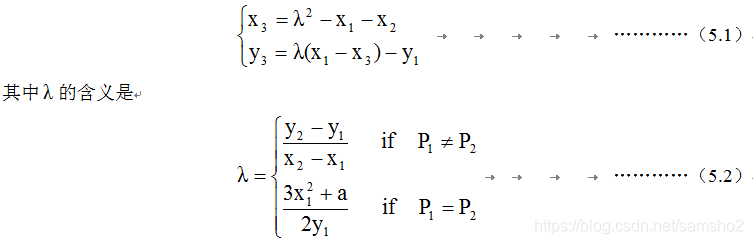
当P1≠P2时,计算P3需要1次逆运算、2次乘法运算和1次平方运算,简记为1I+2M+1S(这里的I表示逆运算,M表示乘法运算,S表示平方运算,下同)。由于素域上的加法和减法比逆、乘法和平方快的多(参见[3],表2),所以可以忽略加法和减法的时耗,甚至小常数(比如2、3)与大整数的乘法也可以忽略不计。
当P1=P2时,计算P3需要1I+2M+2S。
然而,计算素域Fp上的逆是很耗时的(参见[3],§3.6),所以采用射影坐标以尽量避免做逆运算。
这篇关于OpenSSL密码库算法笔记——第5.4.1章 椭圆曲线上点的仿射坐标表示的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!



