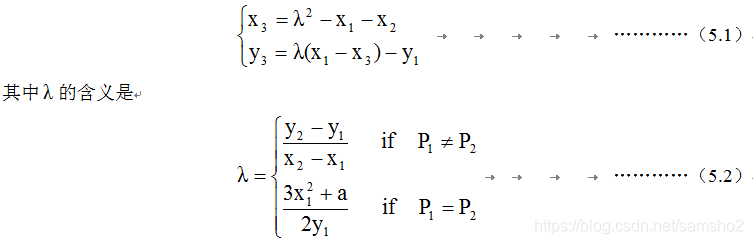http://blog.csdn.net/wirelessqa/article/details/12584043

由上图我们可以知道，在不同的立面坐标系是不同的。在很多业务逻辑处理的时候，需要对不同的立面进行处理，在此封装了一个方法，便于处理不同立面上点的计算。 viewSection 立面或者剖面 point 立面或者剖面上的点 horizontalOffset 点在屏幕中水平方向上的偏移量 verticalOffset 点在屏幕中竖直方向上的偏移量 public XYZ ConvertInViewS

背景：知乎上常有非常精彩的回答/文章，必须要点赞+收藏，日后回想起该回答/文章时翻看自己的动态和收藏夹却怎么也找不到，即使之前保存了链接网络不好也打不开了（。所以我一般碰到好的回答/文章都会想办法保存它的离线版本，但人是懒的，有没有什么办法可以自动保存我点赞/公开收藏过的内容呢。经过苦苦搜寻，终于我找到了这么一个开源的工具： https://github.com/amchii/ZhiArchiv

射影坐标又分成好几种——标准射影坐标、Jacobi射影坐标、Chudnovsky射影坐标。 在标准射影坐标中，射影点(x, y, z)，z≠0，对应仿射点(x/z, y/z)，椭圆曲线的射影方程为y2z＝x3＋axz＋bz2。在Jacobi射影坐标中，射影点(x, y, z)，z≠0，对应仿射点(x/z2, y/z3)，椭圆曲线的射影方程为y2＝x3＋axz4＋bz6。在Chudnovsky射影

椭圆曲线上点的表示分成仿射坐标系表示和射影坐标表示形式，首先来看看仿射坐标表示形式。 素域Fp上的椭圆曲线E由（仿射）方程y2＝x3＋ax＋b决定，设曲线上的两个点为P1＝(x1,y1)，P2＝(x2,y2)，并且记椭圆曲线加法群的单位元为，称为无穷远点或者零点。如果P1≠－P2，则P3＝P1＋P2＝(x3,y3)，可以由如下公式计算出来：

广告关闭 腾讯云11.11云上盛惠 ，精选热门产品助力上云，云服务器首年88元起，买的越多返的越多，最高返5000元！ 因该模块对python3 有兼容性问题，故采用python2.7解释器。 原程序可监听所有事件，现注释掉部分功能，只输出鼠标左键触发的坐标，用于获取坐标，方便自动化取点。 # -*- coding: utf-8 -*-##import pythoncomimport pyho