深入浅出HTTPS协议，RSA算法，对称加密，非对称加密，数字签名，数字证书【包含极简又必不可少的数学推导】

本文主要是介绍深入浅出HTTPS协议，RSA算法，对称加密，非对称加密，数字签名，数字证书【包含极简又必不可少的数学推导】，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

网上大多数介绍HTTPS协议和加密传输的文章都要么过于简洁，要么数学公式过多过于深奥。
本文将以一种更加清楚地结构，从根本原理上介绍HTTPS协议，RSA算法，对称加密，非对称加密，数字签名，数字证书等概念，会包含基础的数学原理，并且保证极其简明扼要

HTTPS 协议

HTTP 的不安全性体现在很多方面，即 HTTP 的缺点。

• 内容被窃听：即使是加密过的通信内容，也会被窥视到，这点和未加密的通信是相同的，只能说经过加密后的内容，即便被攻击者窥视到，他也可能无法破解其中的含义罢了
• 身份被伪装：服务器伪装，客户端伪装，访问权限，无意义请求
• 报文被篡改：完整性不保证，中间人攻击（Main-in-the-Middle attack, MITM）

HTTPS 协议并非应用层的一个新协议，只是 HTTP 通信接口部分用 SSL（Secure Socket Layer）和 TLS（Transport Layer Security）协议代替而已。

另外，SSL 是独立于 HTTP 协议的，所有运行在应用层的协议都可以配合 SSL 协议使用。可以说，SSL 协议是当今世界上应用最为广泛的网络安全技术。

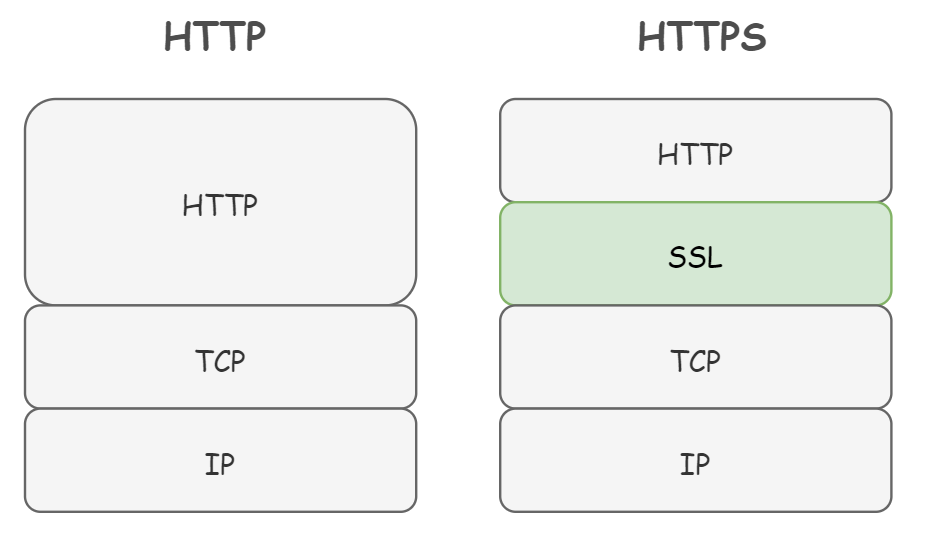
由于使用了加密通信， 相比于纯文本通信的 HTTP 来说，HTTPS 会消耗掉更多的 CPU 及内存资源，另外，开启 HTTPS 需要申请 SSL 证书，高额的证书申购费用会让很多网站开发者望而却步。

加密

密钥：就是钥匙，加密方有一把密钥，用来上锁，解密方也拥有一把密钥，用来解锁。而且加密方和解密方使用的密钥不一定是同一把。

对称密钥

加密和解密使用同一密钥的方式称为对称密钥加密，也称做共享密钥加密（Common Key crypto system）。

以共享密钥加密时必须将密钥也发送给对方。显然，如果通信双方都各自持有同一个密钥，且没有别人知道，则两方的通信安全是可以被保证的（除非密钥被破解），而且效率很高。

那么，最大的问题就是如何保证这个密钥的安全传输，不被外部攻击者知道。如果由服务器生成一个密钥并传输给浏览器，这个传输过程中密钥被攻击者劫持，那么之后攻击者就能用这把密钥解开双方传输的任何内容。因此一般在建立连接时用非对称加密传输共享秘钥，之后通信时再用对称加密方法，即混合加密。

非对称的密钥

加密和解密使用不同密钥。

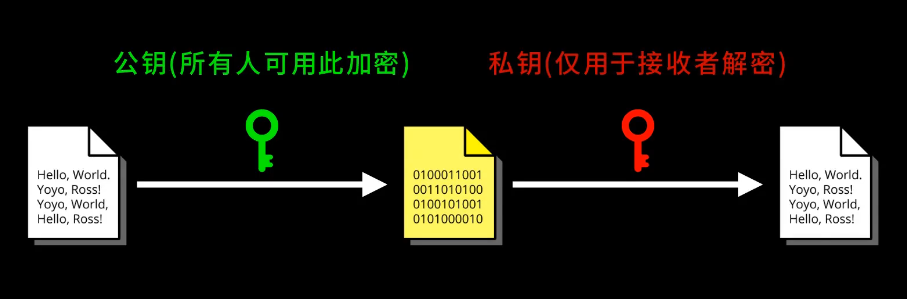
RSA非对称秘钥加密算法

需要一个算法，正向计算容易，但逆向反推难——模运算符合这个特性：计算模简单，但反推指数难，只能穷举（当除数很大时不可取）

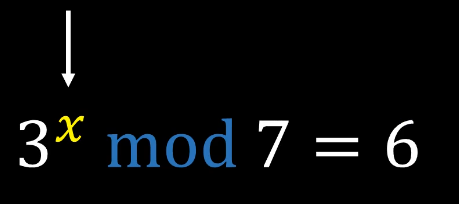
使用模运算即可实现加密解密过程：

合并两式得：

如何选取e和d成为关键。此时要用到欧拉定理：

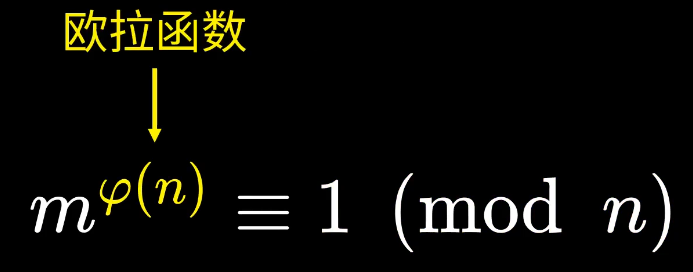
这里的 $\phi (n)$ 表示：小于等于n的正整数中，有多少与n互质的数。将欧拉公式进行变换并对比上式可得下式，其中k为任意正整数

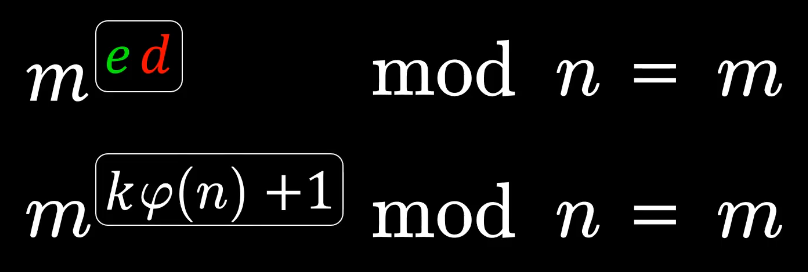
可以通过选取k，n，e，计算得到d：

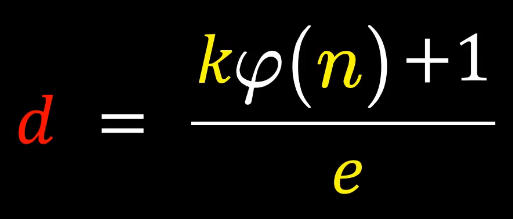
计算 $\phi (n)$ 的一般方法为质因数分解，但大数质因数分解很难。但如果n是一个质数p，则有：

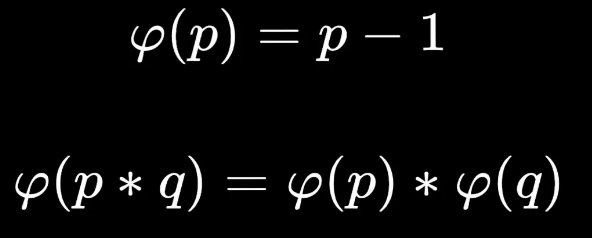
运用到d的计算中：

由于这里的p和q是自己选取，别人不知道，所以无法通过大数n的质因数分解得到p和q，因而无法计算出 $\phi (n)$和 d

数字签名

遗憾的是，混合加密的方式仍然还是有漏洞的。攻击者（中间人）的确无法得到浏览器生成的对称密钥 X，但攻击者完全不需要拿到服务器私有的私钥就能劫持信息！

中间人只需截获服务器发布的公钥，篡改成自己的公钥发给客户端，客户端就会用中间人的公钥加密共享秘钥，中间人再用自己的私钥解密即可获得共享秘钥。根本原因是：浏览器客户端无法确认自己收到的公钥是不是真正的网站服务器的。

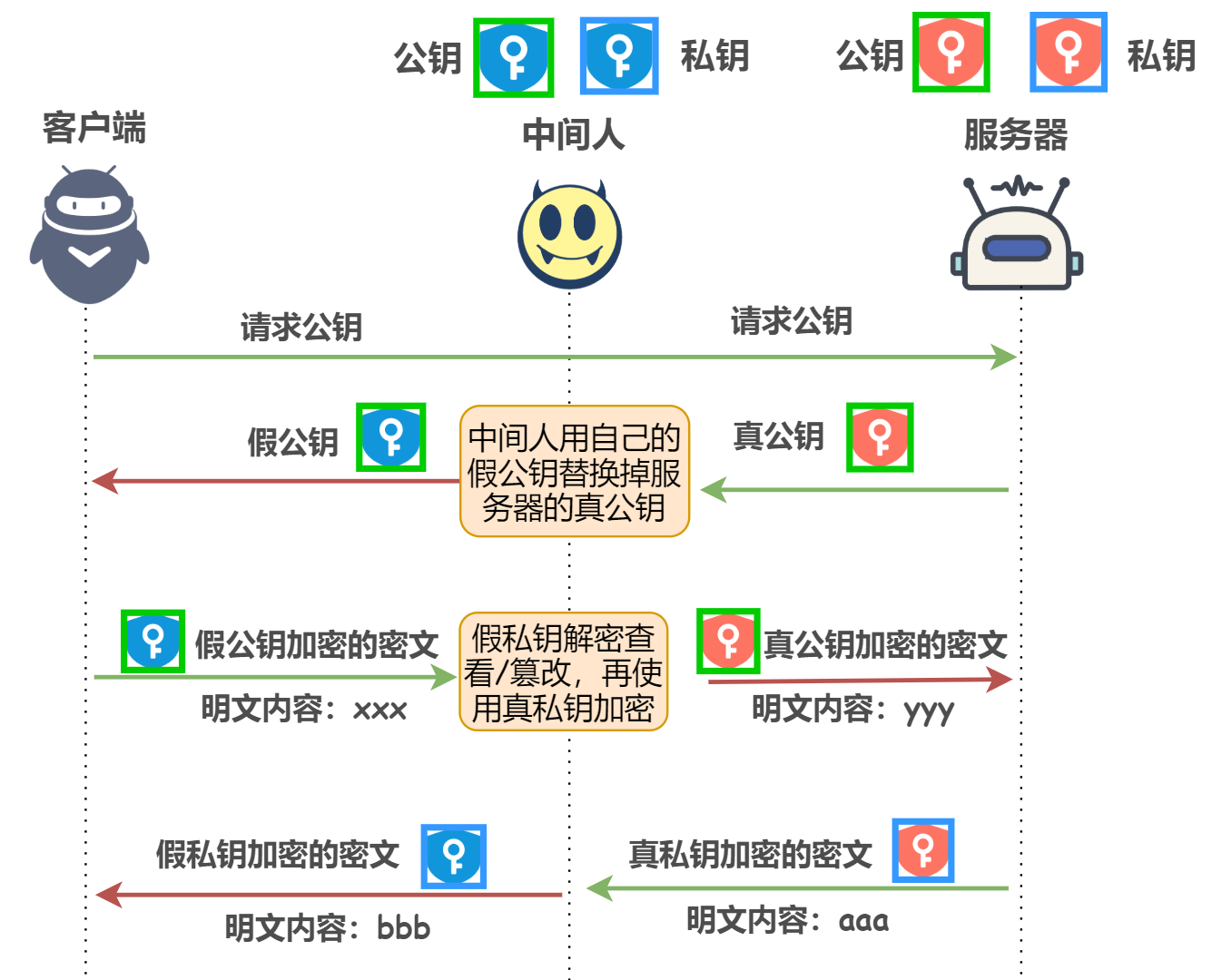
❓ 如何证明浏览器客户端收到的公钥一定是该网站服务器的公钥

服务器在发布公钥和文件时，会同时用私钥将文件哈希值运算得到数字签名，放到网站上。客户端将文件的数字签名和公钥运算得到的文件哈希值与文件本身哈希值对比即可确定文件没有被篡改，并且签名来自于私钥拥有者。

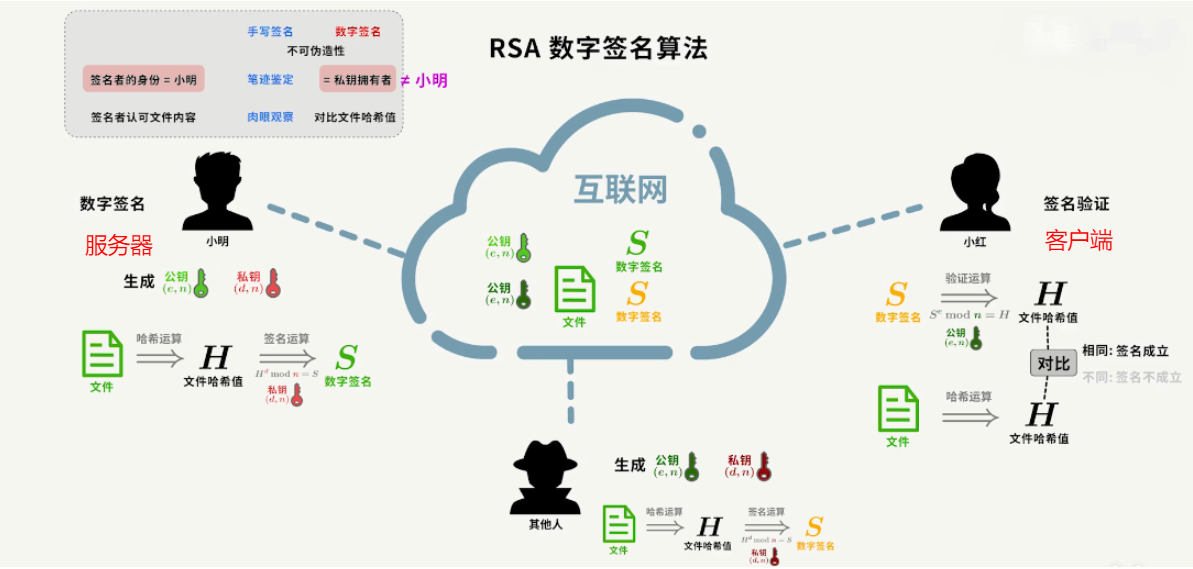
但私钥拥有者不一定等于服务器，因为中间人也可生成一套公钥私钥，对文件签名。客户端验证时使用伪公钥和伪签名对文件进行验证，依旧可以通过。

数字证书

为确保客户端验证时使用的是目的服务器的公钥和数字签名，需要使用公信机构： 数字证书认证机构（Certificate Authority, CA），即客户端和浏览器都信赖的第三方机构。

网站服务器在使用 HTTPS 前，需要向 CA 申请颁发数字证书，数字证书里有证书持有者、证书持有者的公钥，前两者的数字签名等信息。服务器把数字证书明文传输给浏览器客户端，然后浏览器从证书里取出服务器的公钥就可以了。

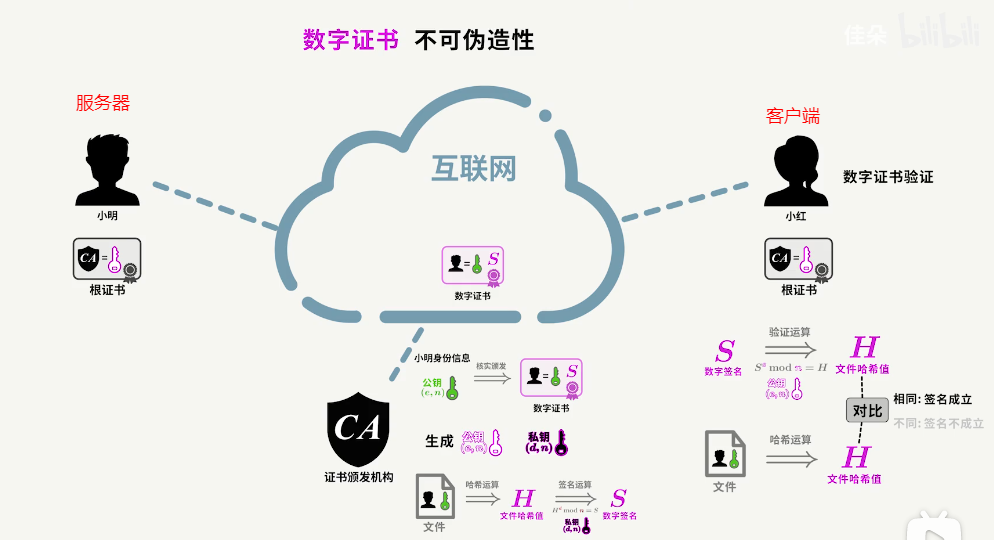
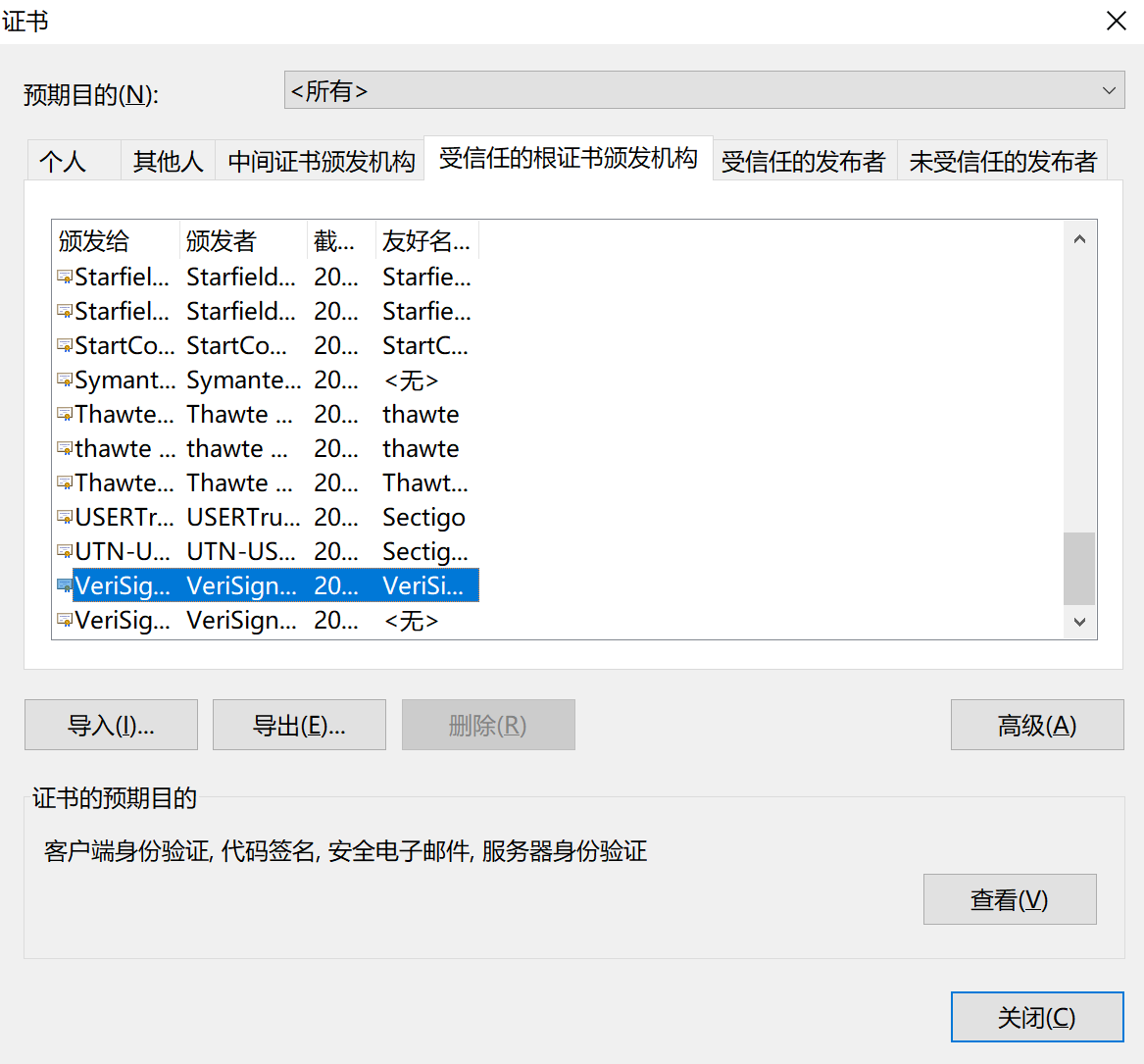
由于计算机里默认安装了根证书，其中包括CA机构的公钥，因此数字证书具有不可为造性。

参考

https://www.bilibili.com/video/BV14y4y1272w?spm_id_from=333.788.top_right_bar_window_history.content.click
https://www.bilibili.com/video/BV18N411X7ty?spm_id_from=333.788.top_right_bar_window_custom_collection.content.click

这篇关于深入浅出HTTPS协议，RSA算法，对称加密，非对称加密，数字签名，数字证书【包含极简又必不可少的数学推导】的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---