本文主要是介绍线性代数中涉及到的matlab命令-第三章：矩阵的初等变换及线性方程组，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！
目录
1，矩阵的初等变换
1.1，初等变换
1.2，增广矩阵
1.3，定义和性质
1.4，行阶梯型矩阵、行最简型矩阵
1.5，标准形矩阵
1.6，矩阵初等变换的性质
2，矩阵的秩
3，线性方程组的解
1，矩阵的初等变换
1.1，初等变换
初等变换包括三种：交换行或列、某行或列乘以一个非零系数、某行或列加上零一行或列的k倍。
1.2，增广矩阵
增广矩阵：方程组的系数矩阵和常数矩阵组成的矩阵。
方程组：
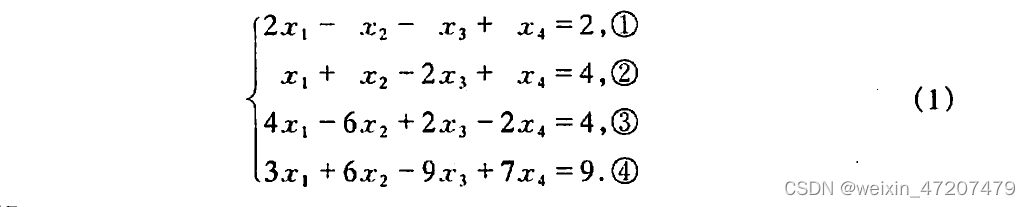
对应的增广矩阵：
1.3，定义和性质
矩阵的初等行变换和初等列变换，统称为初等变换。
待补充：
使用Matlab判断两个矩阵是否等价。
1.4，行阶梯型矩阵、行最简型矩阵
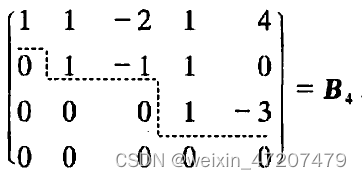
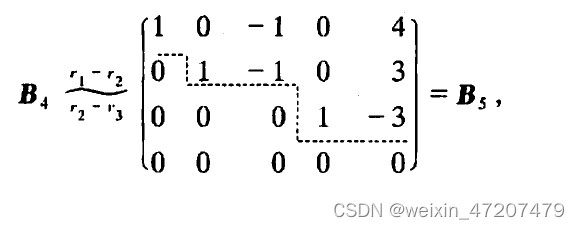
对于任何矩阵，都可以通过有限次初等行变换把它变为行阶梯型矩阵和行最简型矩阵。
利用初等行变换，把一个矩阵化为行阶梯形矩阵和行最简形矩阵，是一种很重要的运算，解线性方程组只需要把增广矩阵化为行最简形矩阵。
Matlab使用rref命令可以得到一个矩阵的行最简形矩阵：
clc;A = [4 2 -1 2;5 2 3 1;11 3 0 8];rref(A)运行结果：
1.5，标准形矩阵
1.6，矩阵初等变换的性质
定义：由单位阵E经过一次初等变换得到的矩阵称为初等矩阵。
三种初等变换对应三种初等矩阵。
第一种：把初等矩阵（单位矩阵两行对调）乘矩阵A，相当于对矩阵A进行初等行变换或列变换（对应的两行或列对调）；
clc;A = [1 1 1 1;2 2 2 2;3 3 3 3]E = eye(3);E1_2 = E;
E1_2(1,:) = E(2,:);
E1_2(2,:) = E(1,:);E1_2E1_2*A运行结果：
上述代码，如果改为右乘初等矩阵，结果为第1列和第2列对调：
clc;A = [1 2 3 4;1 2 3 4;1 2 3 4]E = eye(4);E1_2 = E;
E1_2(1,:) = E(2,:);
E1_2(2,:) = E(1,:);E1_2A*E1_2运行结果：
类似，其他两种初等矩阵乘以矩阵A，相当于对矩阵A做对应的初等变换。
问题：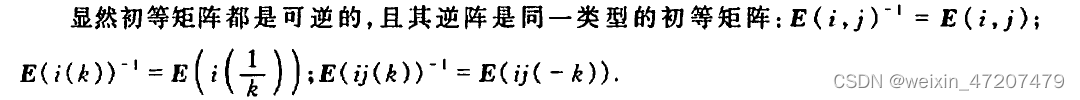
clc;%举例说明E = eye(5);E_23 = E;
E_23(2,:) = E(3,:);
E_23(3,:) = E(2,:); %交换单位矩阵E的2和3行，得到一个初等矩阵A = E_23*E; %E_23*E相当于对单位矩阵E进行了一次初等变化（交换2和3行）得到一个矩阵AB = E_23*A %E_23*A相当于对单位矩阵A进行了一次初等变化（再次交换2和3行）得到一个矩阵B，其实B就是E% B = E_23*A = B = E_23*E_23*E = E 即E_23*E_23 = E，则E_23的逆等于E_23运行结果：
B =1 0 0 0 00 1 0 0 00 0 1 0 00 0 0 1 00 0 0 0 1运行代码发现B还是单位矩阵，即B = E_23*A = E_23*E_23*E = E 即E_23*E_23 = E，则E_23的逆等于E_23，也就是交换行的初等矩阵，它的逆还是它本身。
初等变换得到一个初等矩阵，初等变换的逆变换得到初等矩阵的逆矩阵。
矩阵A可逆，可通过
的方式求A
，因其可转化为
Matlab种使用rref命令可对上述矩阵A和E组成的矩阵转化，将矩阵A对应元素转化为单位阵E，对应的单位矩阵E就变为矩阵A的逆矩阵：
clc;A = [2 -1 -1;1 1 -2;4 -6 5];det(A); %判断A是否有逆矩阵E = eye(3);B = [A,E]rref(B)
运行结果：
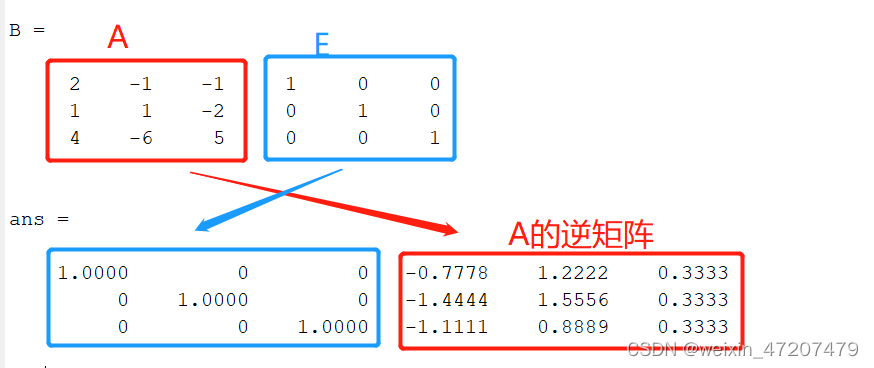
也可使用rref命令求方程组的解：
clc;A = [2 -1 -1;1 1 -2;4 -6 5];b = [4;2;6];B = [A,b]rref(B)
运行结果：
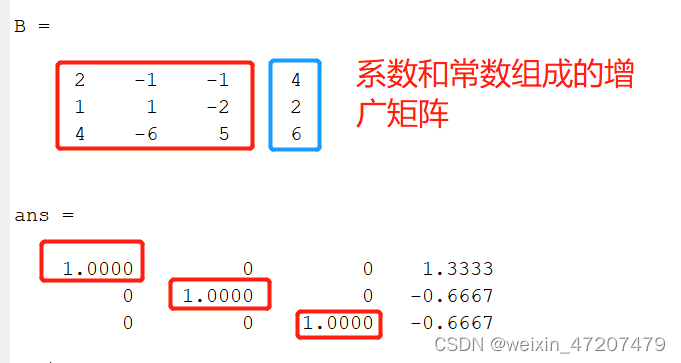
2，矩阵的秩
矩阵k阶子式的概念：
矩阵秩的概念：
矩阵A的秩，A的行阶梯形种非零行的个数。 矩阵的秩用R表示。
如果矩阵A~B，则矩阵A的秩R(A) = R(B)，具体证明可在参考书种找到。
Matlab中计算矩阵的秩的命令为rank。
以下代码中矩阵A经过三种行变换后得到矩阵A12，R(A)=R(A12):
clc;A = [1 3 5 2;2 6 9 0;2 4 1 7]A12 = A;A12(1,:) = A(2,:);
A12(2,:) = A(1,:); %A12为A经过一次行变换后得到，A~A12k = 2;
A12(1,:) = k*A12(1,:); %A12第一行元素乘以kA12(2,:) = A12(2,:) + A12(3,:) %A12第二行元素+第三行元素rank_A = rank(A)rank_A12 = rank(A12) %矩阵A经过三种行变换后的矩阵，他们的秩相同即 A~A12运行结果：
3，线性方程组的解
对于方程组，可通过系数矩阵的秩和增广矩阵的秩判断方程组是否有唯一解，以下代码为判断逻辑：
clc;A = [1 -2 2 -1;2 -4 8 0;-2 4 -2 3;3 -6 0 -6] %系数矩阵b = [1;2;3;4]; %常数矩阵M = rref([A,b])rank(A)rank([A,b])运行结果，系数矩阵的秩和增广矩阵的秩不相等：
很明显增广矩阵的行阶梯形矩阵的第三行是矛盾方程 0 = 1。
这篇关于线性代数中涉及到的matlab命令-第三章：矩阵的初等变换及线性方程组的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！
