本文主要是介绍2020年华数杯数学建模B题工业零件切割优化方案设计求解全过程文档及程序,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
2020年华数杯数学建模
B题 工业零件切割优化方案设计
原题再现:
在大型工业产品中,如机床、轮船、飞机,常常需要很多的小零件,如螺钉、螺帽、螺栓、活塞等。在零件的生产过程中,第一步是需要依照零件产品尺寸从原材料中截取初级产品,这是零件制造的第一道工序。在这道工序中,不同的截取方案具有不同的材料利用率,而原材料的利用率(原材料截取初级产品的总体积与原材料体积之比)直接影响产品的生产成本。在市场上,零件的截面(表面)形状是多种多样的,有圆形、矩形等,零件的厚度(高度)尺寸也是大小不一的。在原材料尺寸固定的前提下,截取零件的初级产品后产生的废料最少是企业的追求。
某零件加工厂新进一种原材料用来加工零件,如表 1 所示。在零件加工的过程中,需要使用切割生产的初级产品如表 2 所示。假设:割缝宽度忽略不计。请你为该零件厂提供如下问题的原材料最优切割设计方案。
问题一:在一块原材料上切割 LJ1 产品,建立数学模型,给出原材料利用率最高的切割方案,即切割的数量和原材料的利用率。
问题二:在一块原材料上切割 LJ1、LJ2、LJ3、LJ4、LJ5、LJ6 产品,建立数学模型,给出利用率由高到低排序的前 5 种切割方案,即每个零件产品的数量和原材料的利用率。
问题三:需要完成表 2 中 LJ1、LJ2、LJ3、LJ4、LJ5、LJ6 产品的生产任务,至少需要多个原材料?由于工艺的缘故,只允许至多采用 5 种切割方案,建立数学模型,给出原材料总利用率最高的至多 5 种切割方案。
问题四:将问题三的产品型号拓展到 LJ1-LJ9, 需要完成表 2 中 LJ1-LJ9 产品的生产任务,同样需要多少个原材料?同样只允许至多采用 5 种切割方案,建立数学模型,给出原材料总利用率最高的至多 5 种切割方案。
问题五:不考虑产品 LJ1-LJ9 的需求数量,给定 100 个原材料,按照表 2 中给出的利润,建立数学模型,给出总利润最大的切割方案(同样要求切割方案不超过 5 个)。

整体求解过程概述(摘要)
在工业零件的生产过程中,最大化地利用原材料是降低生产成本的重要途经。如何有效的提高三维工业零件切割的利用率一直是研究的重点。本文针对不同种类尺寸零件的切割建立混合遗传模拟退火算法优化模型,有效解决了工业零件的三维切割问题。
对于问题一,需给出切割单一型号的产品时原材料利用率最高的切割方案。本文考虑到三维直接切割问题属于 NP-hard 问题,本文通过建堆的方式将问题转换成二维切割问题。在原材料的三个尺寸平面内找到最优切割排列,以单层利用率最高、切割产品数量最多为目标函数,以切割不重叠等为约束条件的多目标的建堆切割模型。通过计算可得,椭圆相切交错排放且选择原料长度和宽度为二维平面时原料的利用率最高,达到89.08%。按照二维最优切割样式逐层切割,得到最后的切割方案可以切割单一型号产品LJ1 的数量为 37386 个。最后,对模型进行了灵敏度分析,在±3%的范围内改变原材料的截面长宽尺寸发现产品数量的变化量不超过2%,说明本文的模型较为稳定。
对于问题二,需给出切割六种产品时材料利用率由高到低的前 5 种切割方案。为简化模型我们按照产品厚度将原材料分层,每层通过外切正六边形对圆等效密集排列。综合椭圆和圆的单一切割模型进行混合切割,以改进后的单层材料利用率最高为目标,以混合排列后的切割方向、切割尺寸和切割不重叠为约束建立二维多物体的切割模型。使用混合遗传模拟退火算法求解,得到利用率最高的前 5 种方案及对应利用率详见表 5.1。当原材料尺寸在±3%内波动时,各方案利用率变化不超过1% ,模型稳定。
对于问题三,在完成生产任务的前提下,给出总利用率最高的至多 5 种切割方案及原材料数量。基于椭圆和圆的混合切割模型增加约束,建立改进后以原材料总利用率最高为目标函数的二维多物体切割模型。总计用去 253 块原材料,具体切割方案见表 6.2。最后,我们对模型进行灵敏度分析,六种产品的生产数量变化不超过1%,模型可靠。
对于问题四,需在完成九种生产任务的前提下,给出总利用率最高的至多 5 种切割方案及原材料数量。本文对规则长方体进行三维切割建模,得到利用率最高的切割方式。将零件单一切割时的利用率作为比例系数对原材料进行区域划分,零件需在各自区域内以最佳的切割方式切割。我们建立以原材料总利用率为目标函数的三维多物体切割模型,总计用去 295 块原材料,具体切割方案见表 7.2。最后,对模型进行灵敏度分析,在±3%的范围内改变截面长宽尺寸,九种产品的生产数量变化不超过1%,模型稳定可靠。
对于问题五,需给出 100 个原材料能实现最大利润的切割方案,不考虑产品 LJ1-LJ9的需求数量。基于问题四,增加原料总数的约束,建立以原材料利润最高为目标函数的三维多物体切割模型,求得只切割 LJ7 的利润最大,最大利润为 216507200 元,具体切割方案见表 8.2。最后,在灵敏度分析中,当分层截面的长改变±3%,模型计算出的 LJ7产品的利润量变化不超 1%,模型具有一定的普适性。
最后,本文对所建立的模型和求解方法的优缺点给出了评价,并结合实际对模型的推广加以分析。
模型假设:
根据零件加工的特点与问题的背景,针对于本题,我们做出以下假设:
1)不考虑原材料切割时产生的损耗;
2)原材料可以沿着任意方向切割;
3)多块原材料不能重叠在一起或拼接在一起使用;
4)在利润估算时,是考虑原材料的成本,不考虑切割成本;
模型的建立与求解
问题一要求在原材料上仅切割单一型号的产品 LJ1,并给出原材料利用率最高的切割方案。考虑到三维直接排样的复杂性,本文采用建堆方法将其转换成二维零件切割问题。首先需要确定长、宽、高三个方向上任意组合的最优切割方案,然后按照最优切割方案逐层进行切割,从而达到降维的效果。由于产品表面形状为椭圆,可将其等效成长方形进行规则排布,也可利用椭圆间相切的性质进行紧密排布。因此,本文建立了以二维平面利用率最高、切割产品数量最多为决策目标,以原材料分层截面的尺寸大小等条件为约束的多目标切割模型,并对其进行求解。最后,本文进行模型的灵敏度分析,改变分层截面的长或宽,使其在[−3%, 3%]的区间内变动,记录求得的 LJ1 产品数量的变化情况。
选取决策变量
分层切割模型
由于原材料𝑆仅用作切割 LJ1,为简化模型,本文首先采用分层的方式将三维切割问题转换成二维切割,即按照产品任一尺寸大小(长𝐿、宽𝑊、高𝐻)为切割厚度对原材料任一方向(长𝑙、宽𝑤、高ℎ)进行分层切割。下图即为原材料分层的三个切割方向:
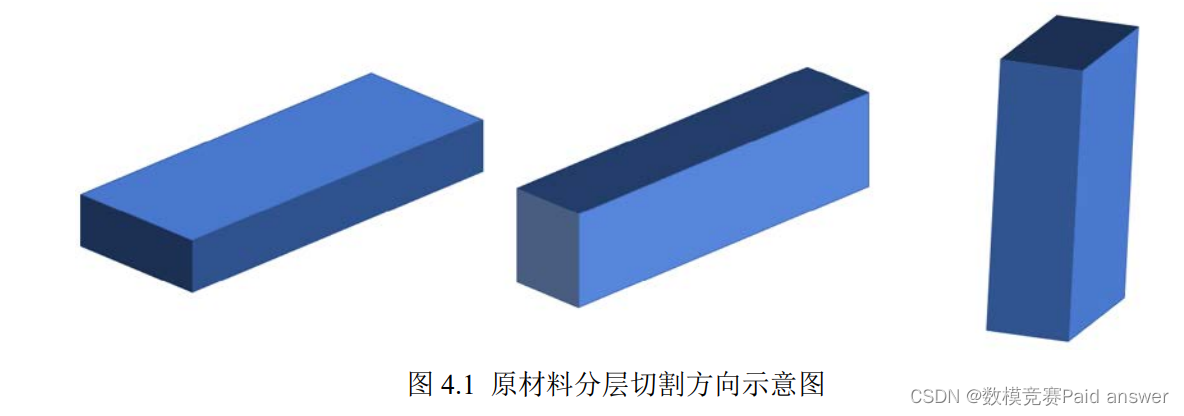
任意选择一个切割方向,以第二种为例,每层的切割厚度根据产品尺寸又存在三种选择,下图分别是以椭圆的短半轴、长半轴和厚度作为分层厚度切割的示意图:


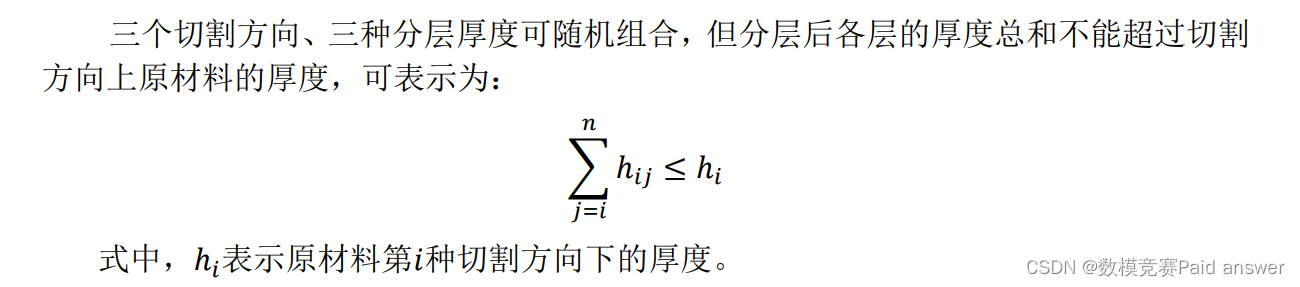
二维切割模型


不规则切割
当椭圆柱体的厚度作为分层厚度时,在该层截面上需切割的图形为椭圆形。针对椭圆,本文可将其置于一个矩形内进行规则切割,可借鉴规则切割,但这种方法会产生很多废料,原材料利用率不高。此外,本文还可以利用椭圆的相切性质密集切割,利用率明显提高,两者废料剩余情况如下图:
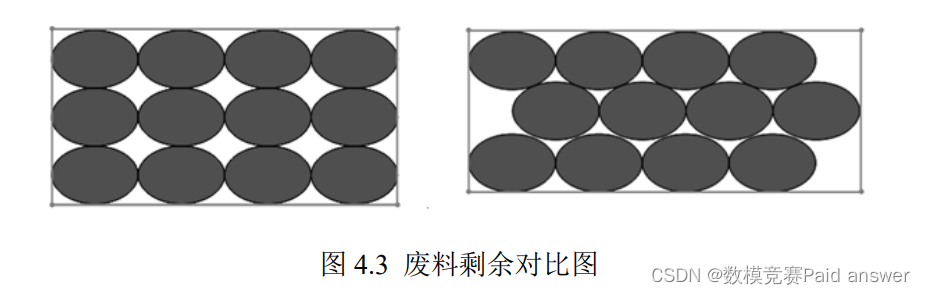
图中黑色区域表示零件的区域,其余的空白为剩余的废料。本文就密集切割展开研究,下图为椭圆密集排列的局部示意图:
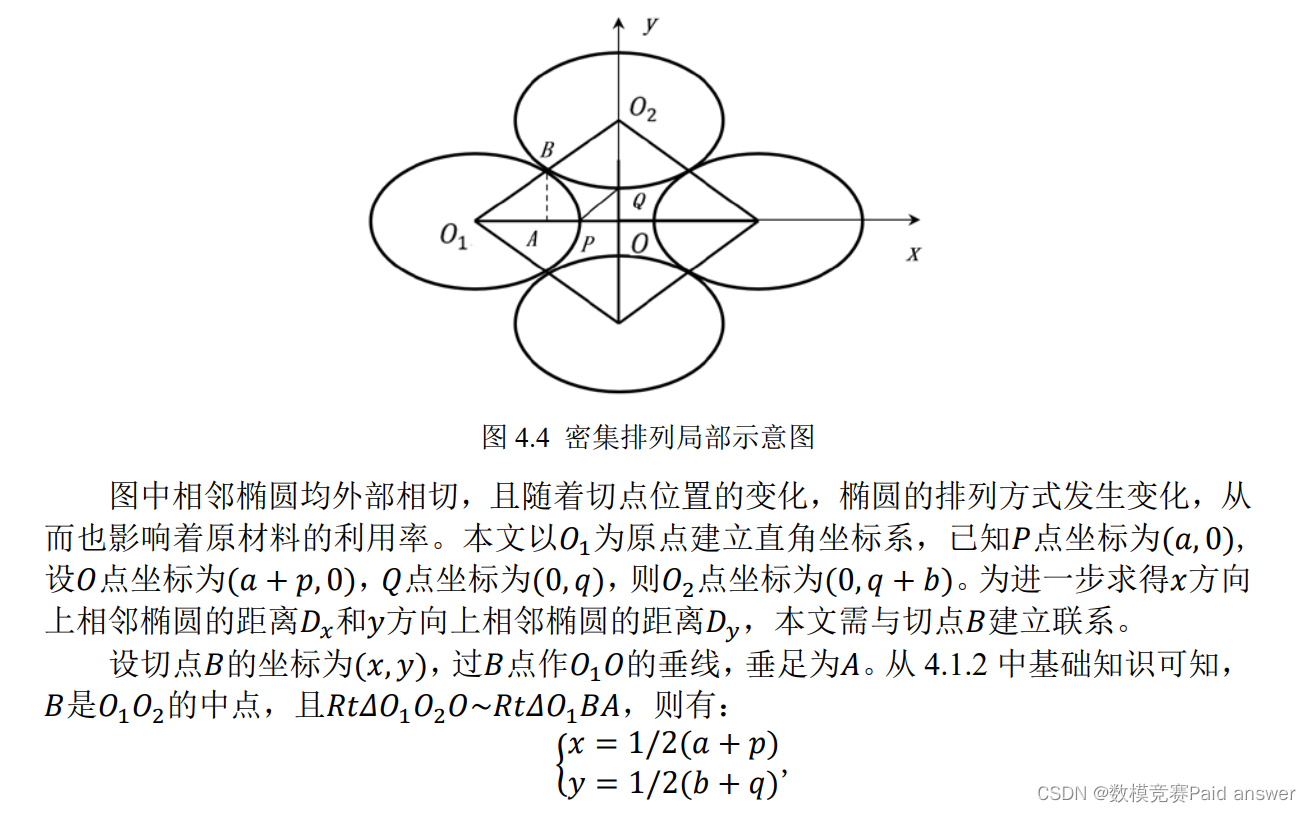
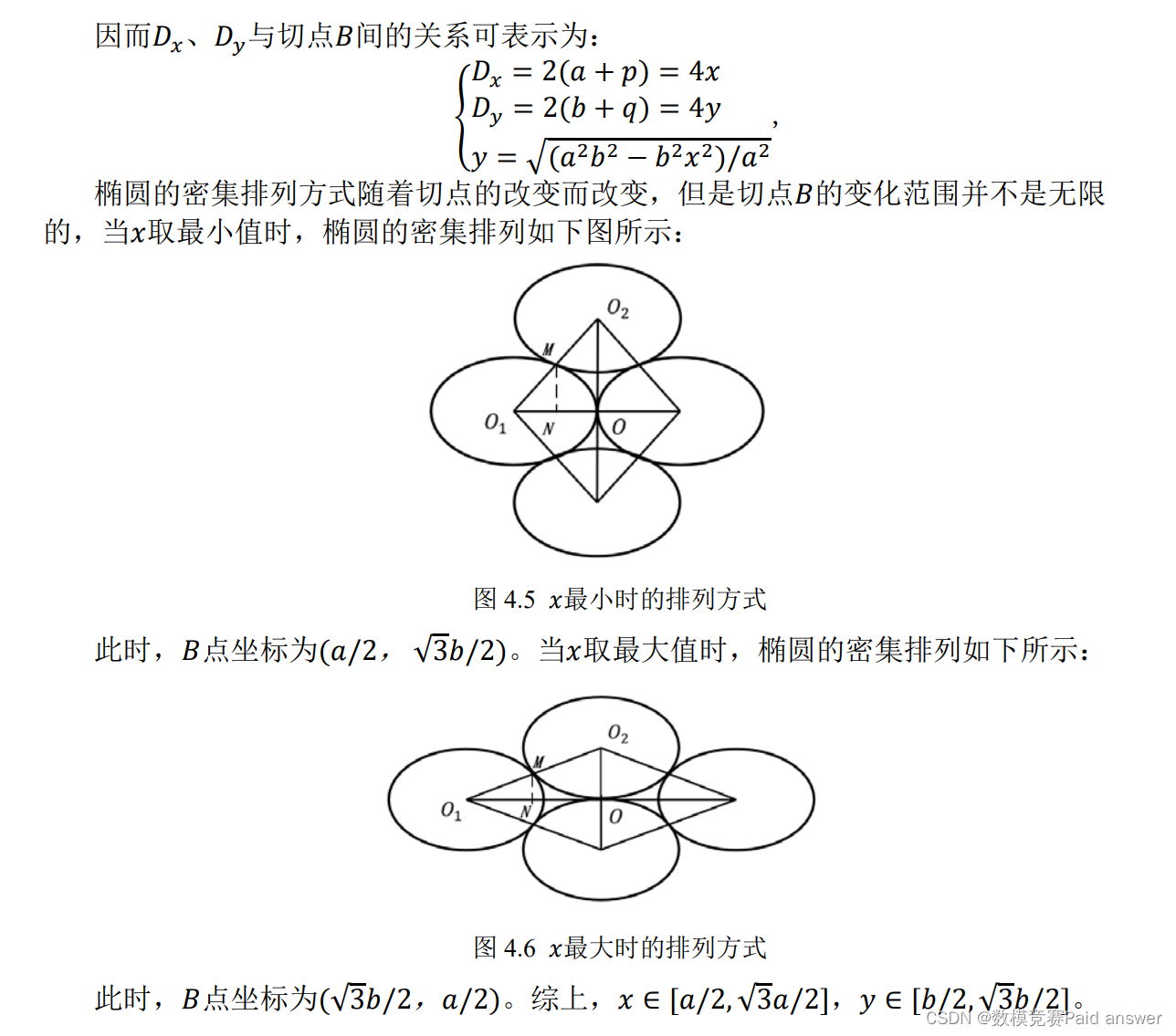


模型求解

分层切割模型求解
考虑到需要切割的形状不规则,分层切割的层数越多,在分层材料边角处造成的损耗越大。因此,计算过程中本文仅在原材料截面面积最大的面上排列切割,将原材料的尺寸、正椭圆柱体的横径、竖径、厚度等相关参数代入分层切割模型中,按照不同的排列方式得到原材料利用率结果如下表所示:

此时分层利用率为可利用的分层原材料与总原材料的比例。实验发现,当将 6060 边作为椭圆的长轴方向,2160 边作为椭圆的短轴方向,240 边作为高度分层,每三个椭圆相切排列,此时的分层原材料利用率最高,为 89.08%。具体的三种排列方式如下图所示,abc 分别表示三种不同的排列方式,且原材料利用率依次递增。
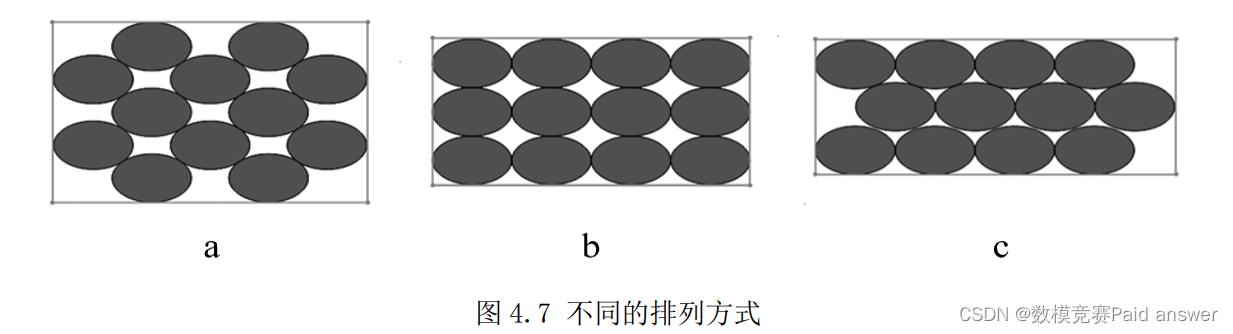
观察上图的排列方式以及对应的原材料利用率可知,椭圆不同排列方式对原材料利用率的影响,图中均为 12 个椭圆,利用率从左到右依次递增。采用 c 排列方式时,原材料利用率可以达到 89.08%。因此在下面零件切割设计方案中,选用的是图 4.7-c 表示的排列方式。
切割模型求解
针对所有分层原材料,本文直接将相关参数代入模型中进行求解计算,得到最终产品的数量以及原材料利用率如下所示:

经过优化计算,本文得出一块原材料 S 最多可生产 37386 件 LJ1 初级产品,原材料利用率高达 89.08%。此时具体方案为将原材料的 240mm 作为高度进行分层切割,每一层奇数行排列 101 个椭圆,偶数行排列的椭圆数比技术行少 1,为 100 个,一共 62 列,一共可以得到 37386 个 LJ1 产品,整体原材料利用率为 89.08%
灵敏度检验
为了检验模型的稳定性,我们把原材料的长度调整±3%,观察计算结果是否会出现较大的改变,检验结果如下所示:
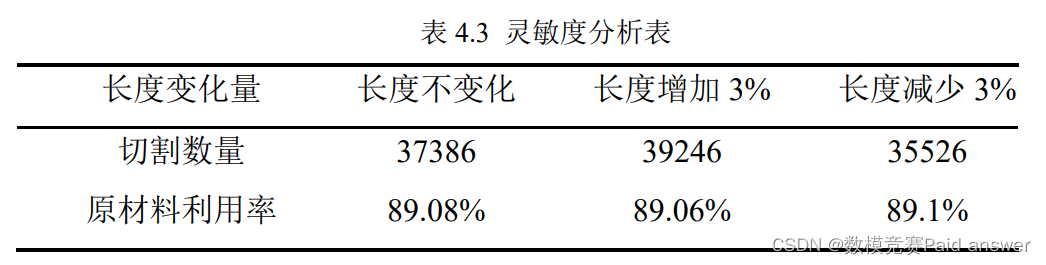
根据结果本文可以看到,当原材料的长度增加或者降低 3%,LJ1 的切割数量改变量不超过 3%,原材料利用率改变量不超过 0.1%,基本不发生变化。由此可见,本文的模型较为稳定。
问题二在一块原材料上切割 LJ1、LJ2、LJ3、LJ4、LJ5、LJ6 产品,要求对切割方案进行优化,给出利用率由高到低排序的前 5 种切割方案。由于 LJ1、LJ2、LJ3、LJ4、LJ5、LJ6 的厚度均 40,因此第二问可以采用建堆法的方式将三维的零件切割问题转为二维的平面切割问题。同时该问题并没有对每个零件的产品数量进行限定,其目标仅为得到最高的原材料利用率。根据上一问可以得知规则切割的原材料利用率比不规则切割的利用率高,在本文中可以将零件进行规则排布。由于本文的优化目标是最高的原材料利用率,因此将问题转为原材料二维截面上的零件切割总面积最大的问题进行求解。
模型建立

目标函数建立


模型求解
初始位置的选择

混合遗传模拟退火算法
零件切割问题难以在规定时间内得到精确解,该问题属于 NP-Hard 问题。在求解NP-hard 问题中,遗传算法有着不错的表现,有较好的全局搜索能力。但是遗传算法在局部搜索与收敛速度方面效果不是很明显,而模拟退火算法则在局部搜索中展现出较好的能力。因此本文采用二者结合的方法来解决零件切割问题,并且算法中融入了最优解保存策略来提高性能。
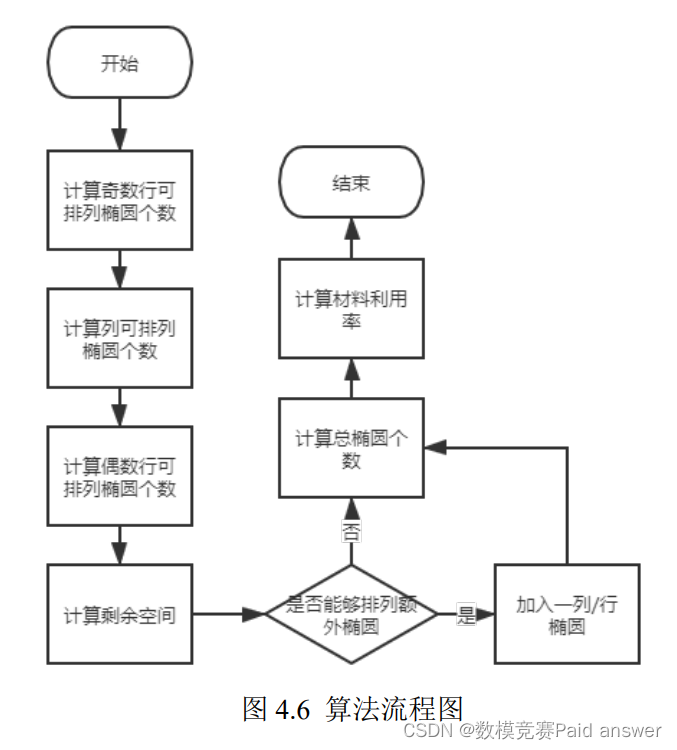
因此,我们设计了一套基于切割序列的混合遗传模拟退火算法。算法总共包含两个阶段。第一阶段是先通过基于各零件的切割坐标序列的启发式算法生成初始的装载方案,为后续方案的优化提供较好的初始解;第二阶段是采用模拟退火算法对零件切割方案进行优化。通过遗传算法与模拟退火结合的方式能够获得优化切割方案,算法的总体流程如下图所示:
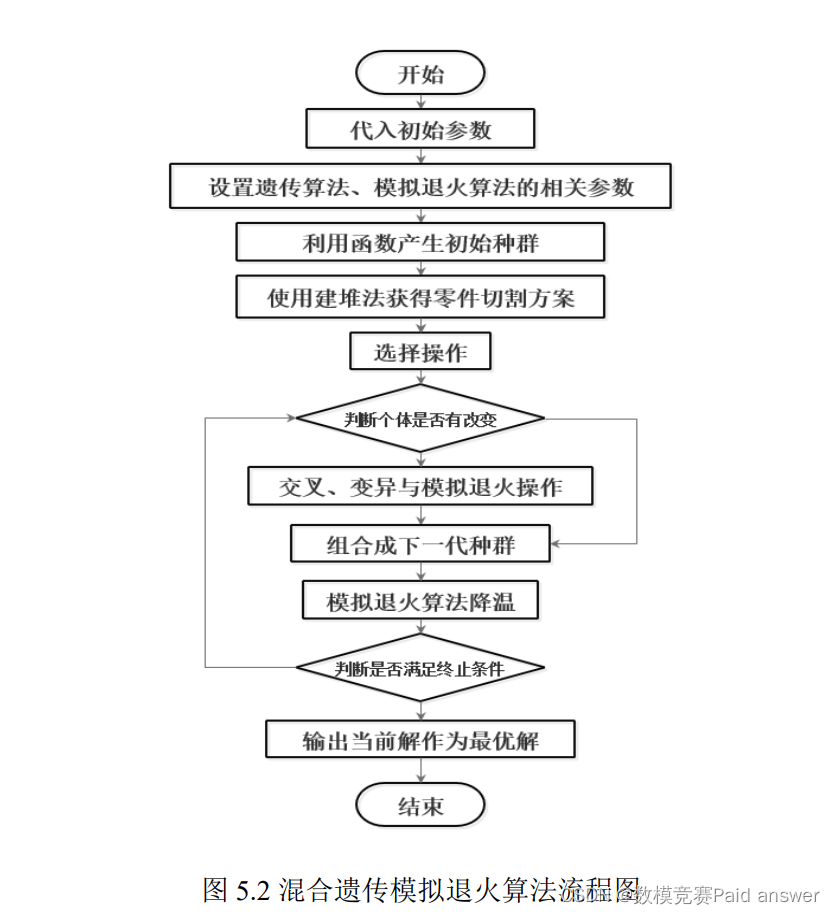
算法求解
根据问题 2 的零件切割模型,以及上文提出的算法流程,利用 matlab 编程,将相关参数带入得到问题 2 的结果为:
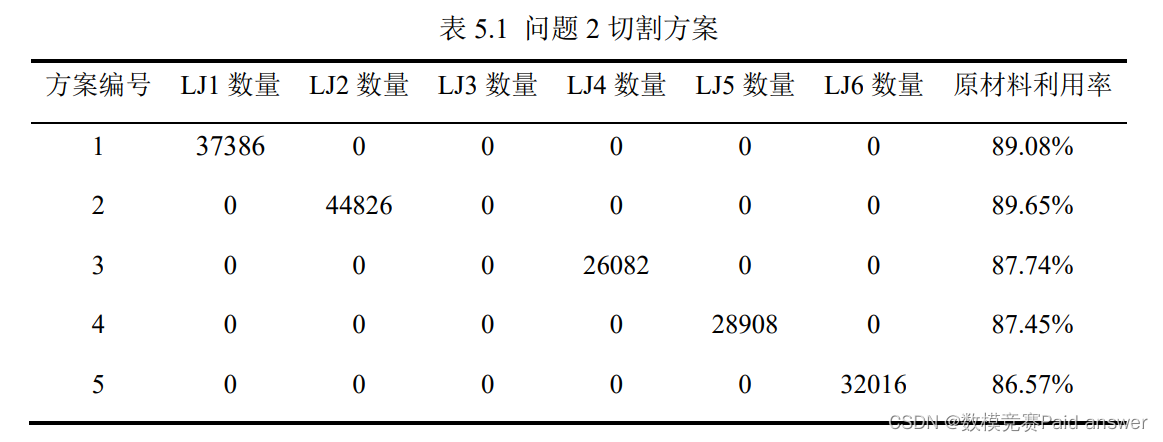
题目中要求给出在一块原材料上切割六种产品利用率最高的方案,并未提及六种需生产的件数。因此我们以利用率最高为目标,求解得出原材料利用率最高的方案为 LJ2产品的单一切割,该方案的利用率为 89.65%。此外,结果中也出现了两种及以上产品混合切割的情况,但其利用率不高,本文仅选取利用率最高的前5种方案列入上表中展示。
灵敏度检验
为了检验模型的稳定性,我们把原材料的长度改变[−3%, +3%],观察计算结果是否会出现较大的改变,检验结果如下所示:
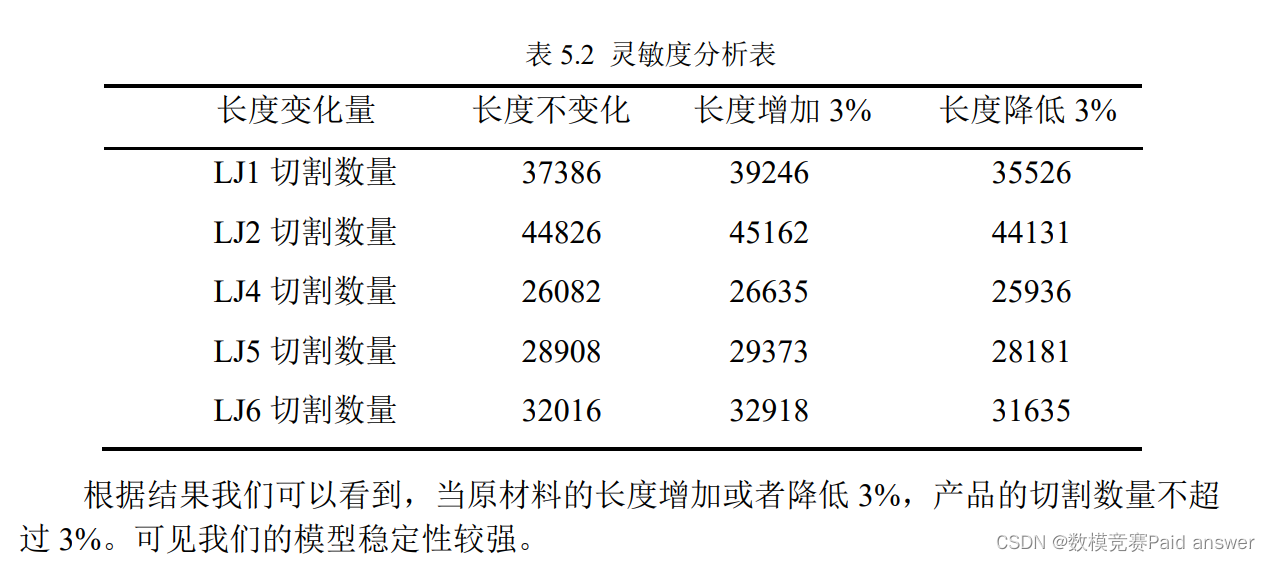
问题三与问题二加工的产品相同,均为 LJ1、LJ2、LJ3、LJ4、LJ5、LJ6,但对各个产品的数量进行了限制,要求满足生产任务的需要,且至多采用 5 种切割方案。要求给出原材料利用率最高的方案。由于生产任务所需要的产品数量是固定的,所以原材料利用率主要由完成任务说需要的原材料个数所决定。原问题转化为,在不超过 5 种切割方案时,求完成生产任务所需要的最少的原材料数量。
通过观察 LJ1、LJ2、LJ3、LJ4、LJ5、LJ6 这 6 种产品的规格可以发现,其高度均为40mm,且形状均为椭圆体(圆柱体可以看做椭圆体的特例)。结合之前问题所求出的较优解为产品在高度上堆叠而成,所以该问题可分解为将原材料分层,每一层分别加工某一种产品,最后求在最多 5 种切割方案限制下,完成生产任务花费原材料最少的分层组合方案。
模型建立
变量说明

模型建立

模型求解
每层可切割数量
每一层可切割产品的数量可使用类似问题 1 中的方法得出。由于问题 1 使用的是分层的方案,而每一层中切割方法都相同,所以这里只取其一层,经过计算,每个产品每层可切割数量如下表所示:
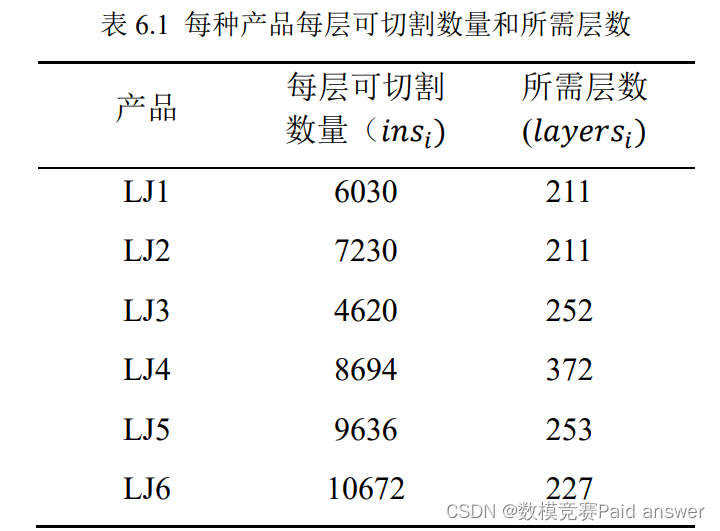
从上表可以看出,LJ1 和 LJ3 所需层数相同,且和 LJ6 所需层数相近。LJ3 和 LJ5 所需层数相近,LJ4 所需层数最多,设计方案时需要注意。
整体求解
在确定好每类产品所需要的层数之后,即可将六类分层方式组合成最多 5 种组合之中。在这里,我们贪心得使排列组合中,每类产品所占的层数占比与所需层数的比例接近,且优先照顾需求量较大的产品。针对需求量较为接近的产品,应尽量安排在同一原材料中以减少原材料浪费。
经过模型求解,得到如下的分配方案:
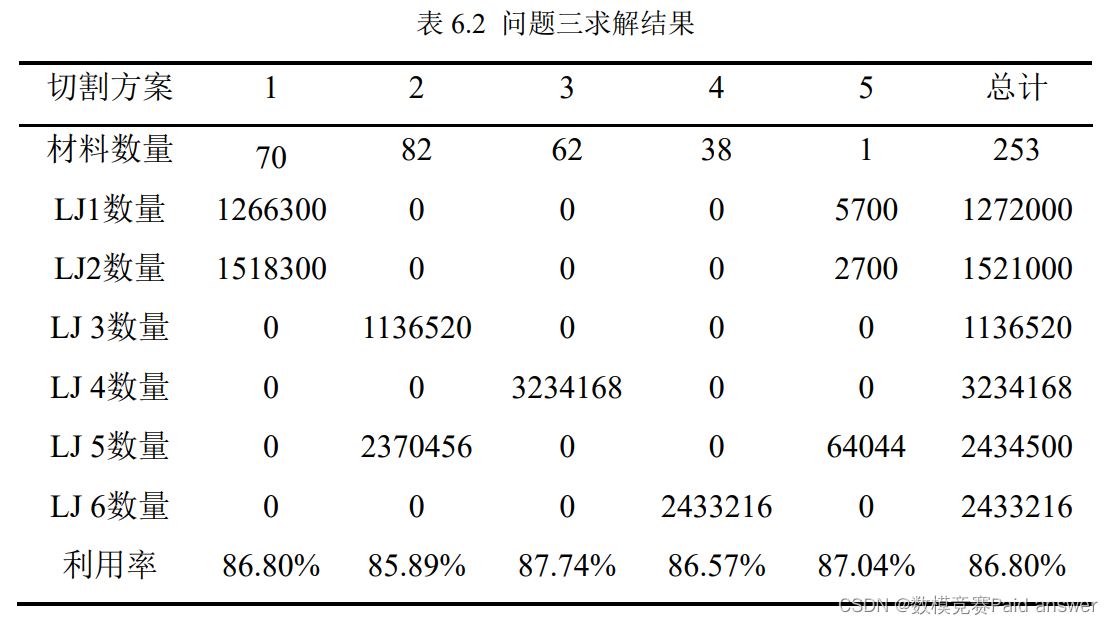
由上表可得,每种产品单独分割时原材料的利用率最高,因此我们尽量使每种产品单独生产,同时对原材料利用率较高的单一切割方案加以改进,使其实现多物体切割。最终我们求解得出:方案三和四分别用于 LJ4 和 LJ6 产品的单一切割,分别用去 62 块和 38 块原材料,利用率分别为 87.74%和 86.57%;方案一用于 LJ1 和 LJ2 产品的混合切割,用去 70 块原材料,利用率为 86.80%;方案五用于 LJ1、LJ2 和 LJ5 产品的混合切割,用去 1 块原材料,利用率为 87.04%。总计用去 253 块原材料,完成了六种产品的生产任务,且利用率最高。
灵敏度检验
为了检验模型的稳定性,我们把原材料的长度增加、降低 3%,计算结果是否会出现较大的改变,检验结果如下所示:
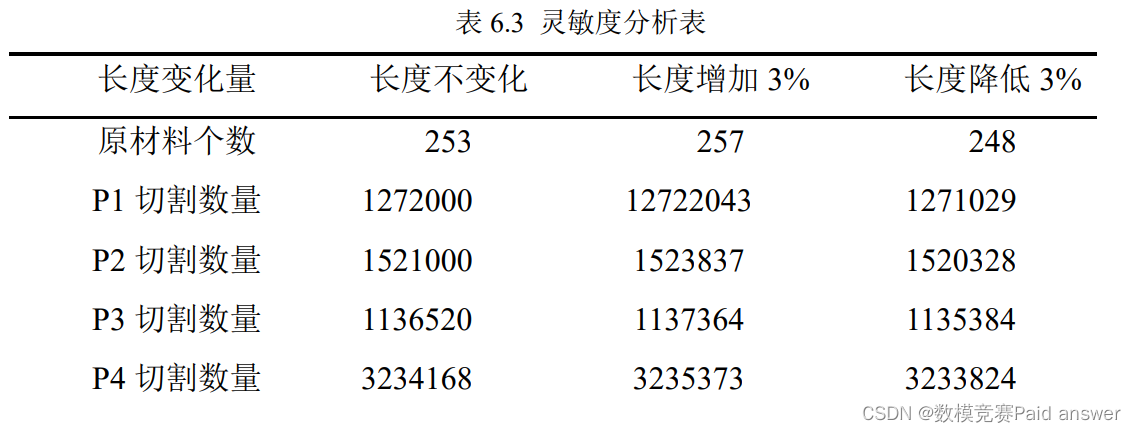

根据结果我们可以看到,当原材料的长度增加或者降低 3%,产品的切割数量变化不大,原材料所需要的个数降低或降低 3%,可见我们的模型稳定性较强。
问题四在问题三的基础上增加了 LJ7、LJ8 和 LJ9,即在最多 5 种切割方案的限制下,求完成 LJ1至LJ9 生产任务所能达到的最大原材料利用率。同问题三一样,由于生产任务数量固定,所以仍可以转化为求所需原材料数量最少的方案。但由于LJ7~LJ9是长方体,且高度各不相同,所以分层的排列组合方式会略有不同。
观察可以发现,LJ1~LJ6、LJ7、LJ8、LJ9 的高度分别为原材料高度的 1/6、1/2、1/3、1/4,即经过相应的排列组合后,依然可以采用高度分层的方法来进行求解,问题再一次转化为将原材料分层,每一层分别加工某一种产品,求在最多 5 种切割方案限制下,完成生产任务花费原材料最少的分层组合方案。
由于问题的相似性,我们采用与问题三类似的变量定义,这里产品类型将由 1至6 拓展为 1至9,。由于 LJ1至LJ6、LJ7、LJ8、LJ9 的高度分别为原材料高度的 1/6、1/2、1/3、1/4,我们可以将原材料的高度划分为 12 份,则 LJ1~LJ6、LJ7、LJ8、LJ9 高度分别占据2、6、4、3 份。
模型建立

模型求解
因每种产品的格子数不同,类似于背包问题,但这里优化的目标为背包数量最少。将不同产品排列组合到背包(原材料)中,这里依然使用启发式方法,计算出每种产品所需要的层数,层数相近的产品优先组合到一种切割方案中。
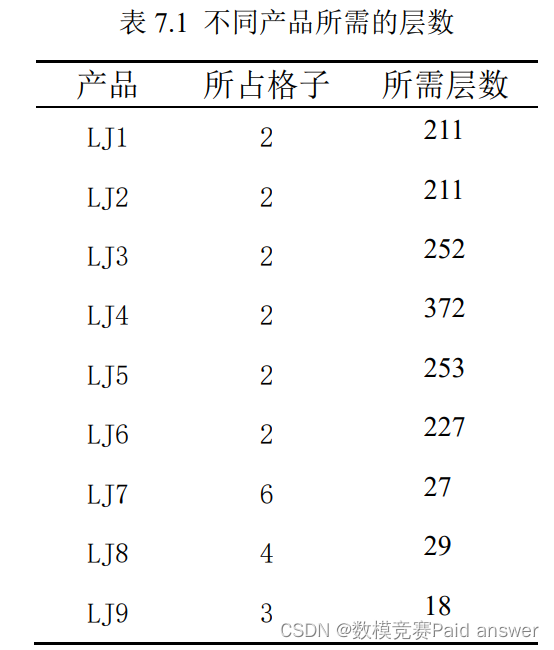
由表中可以看出,虽然 LJ7、LJ8、LJ9 所占格子数量较特殊,但由于其截面较小,所需的层数并不多。5 种切割方案中,每个切割方案都有 12 层,问题可描述为求一组 9个产品 5 组的排列组合方案,似的完成所需层数所需要的原材料最少,最终结果如下:
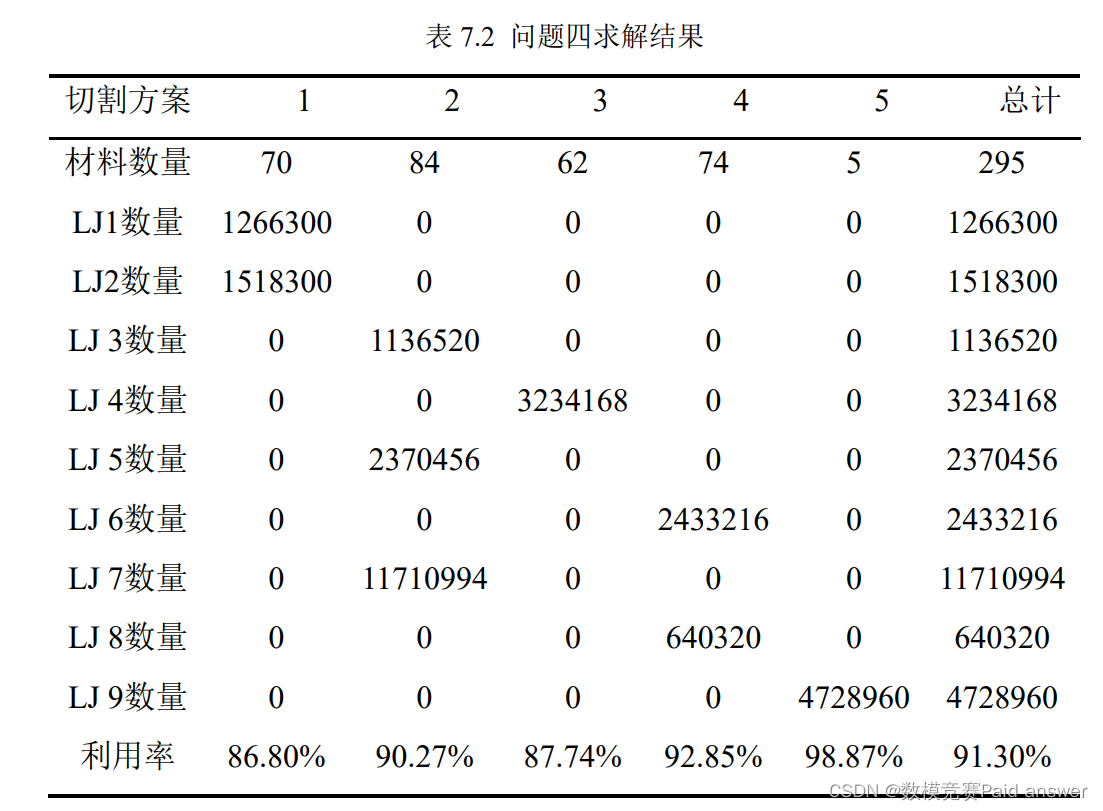
由上表可得,方案一用于 LJ1 和 LJ2 产品的混合切割,用去 70 块原材料,利用率为 86.80%;方案二用于 LJ3、LJ5 和 LJ7 产品的进行混合切割的方式切割,用去 84 块原材料,利用率为 90.27%;方案三用于 LJ4 产品的单独切割,用去 62 块原材料,利用率为 87.74%;方案四用于 LJ6 和 LJ9 产品的混合切割,用去 74 块原材料,利用率为92.85%;方案五用于 LJ9 产品的单独切割,用去 5 块原材料,利用率为 98.87%。总计用去 295 块原材料,完成了九种产品的生产任务,且利用率最高。在模型的灵敏度检测方面,为了检验模型的稳定性,我们把原材料的长度增加、降低 3%,观察计算结果是否会出现较大的改变,检验结果如下所示:
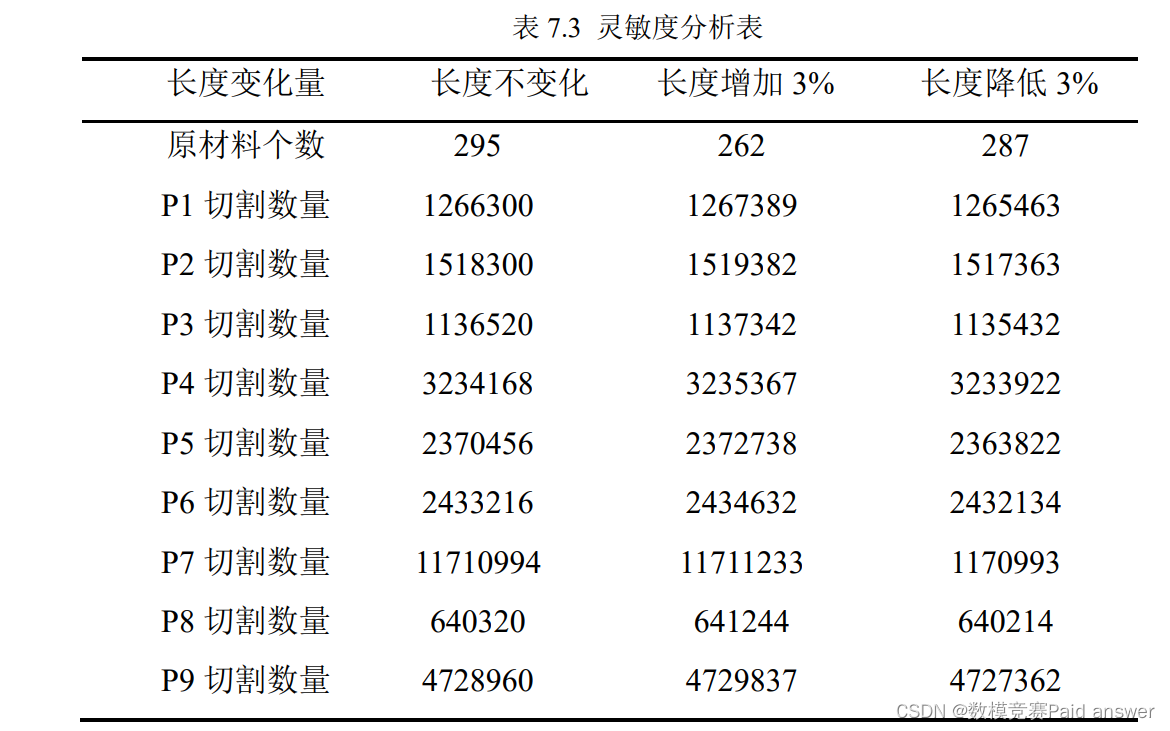
根据结果我们可以看到,当原材料的长度增加或者降低 3%,产品的切割数量变化不大,原材料所需要的个数降低或增加约 3%。因此,我们的模型稳定较强。
问题五在 100 块原材料上面切割 LJ1、LJ2、LJ3、LJ4、LJ5、LJ6、LJ7、LJ8、LJ9产品。问题五每个型号的零件数量没有限制,但是要保证这批原材料切割出的零件的总利润最大。且在原材料成本固定,不考虑零件切割的加工费的前提下,找出总利润最大的切割方案。
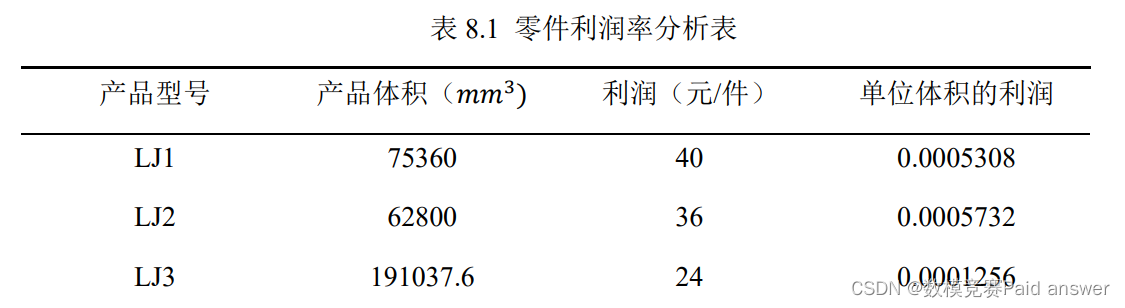
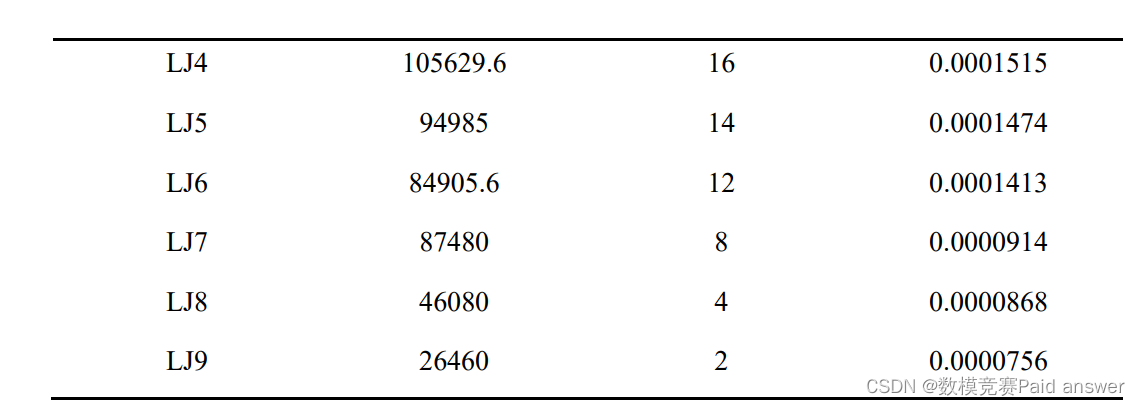
由上图的不同型号的零件利润率表可知,单位体积下的利润不同。因此在对切割方案进行优化的过程中,可以优先选择利润率较高的型号。同时由于不同的型号的厚度不同,在保证较高的利润就需要优先选择厚度相同的零件,或多个零件堆叠保证厚度相同,这样可以保证较小的原材料耗费,能流出更多的空间切割零件。基于这种思路,对问题五的模型和算法进行设计。
模型建立

模型求解
位置选定算法


算法求解
已知问题五的模型,将参数带入。通过位置选定算法获得初始方案,并通过混合遗传模拟退火算法对方案进行优化,利用 matlab 编程,最终得到的在 100 块原材料中利润最高的方案为:

经过优化计算,本文得出 100 块原材料上切割总利润最大为 216507200 元,其中只需要切割 LJ7,切割数量为 28563400 个。
灵敏度检验
为了检验模型的稳定性,本文把原材料的长度改变±3%,观察计算结果是否会出现较大的改变,检验结果如下所示:
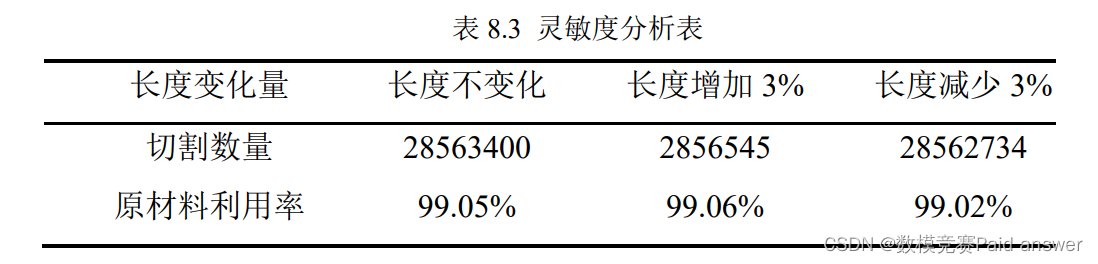
根据结果本文可以看到,当原材料的长度增加或者降低 3%,LJ1 的切割数量改变量不超过 3%,原材料利用率改变量不超过 0.1%,基本不发生变化。由此可见,本文的模型较为稳定。
论文缩略图:


程序代码:
clc,clear,close all
% 定义全局变量
global box oval
box.x = 6060;
box.y = 2160;
box.z = 240;
oval.a = 30;
oval.b = 20;
oval.h = 40;
% 计算 x 方向偶数列放几个,并下取整
count_x_1 = floor(box.x/(oval.a*2));
% 记录余量
box.x_remain_1 = box.x - oval.a*2*count_x_1;
% 交错排放,奇数列数量减 1
count_x_2 = count_x_1 - 1;
% 计算奇数列的余量
box.x_remain_2 = box.x - oval.a*count_x_2 + oval.a;
%判断偶数列余量是否还可以放一个
if box.x_remain_1 > oval.a*2 count_x_2 = conut_x_2 + 1;
end
% 计算奇数每列放的数量
count_y_1 = floor(box.y/(oval.b*2*(sqrt(3)/2)));
% 判断偶数列放的是否为偶数
if mod(count_y_1,2) == 0 num = count_y_1/2*(count_x_1+count_x_2)*(box.z/oval.h);
else num = ((count_y_1-1)/2*(count_x_1+count_x_2)+count_x_1)*(box.z/oval.h);
end
% 计算利用率
material_percentage = num*oval.a*oval.b*pi*oval.h/(box.x*box.y*box.z);
disp('LJ1 椭圆排列情况:')
disp(['数量:',num2str(num),'个']);
disp(['奇数行排列零件个数:',num2str(count_x_1),'个']);
disp(['偶数行排列零件个数:',num2str(count_x_2),'个']);
disp(['奇数列排列零件个数:',num2str(count_y_1),'个']);
disp(['偶数列排列零件个数:',num2str(count_y_1 - 1),'个']);
disp(['原料利用率:',num2str(round(material_percentage*100,2)),'%']);
%% 问题二的求解
clear;clc;
%初始化原料参数
global box circle ellipses %cubes
box.x = 6060;
box.y = 2160;
box.z = 240;
%椭圆参数 LJ1 和 LJ2
EllipsesParameters = [60, 40, 40; 50, 40, 40];
% 圆形的参数
CircleParameters = [78, 40; 58, 40; 55, 40; 52, 40];
% % 长方体的参数 问题二中没有长方体
% CubesParameters = [27, 27, 120;
% 24, 24, 80;
% 21, 21, 60];
% 结果的输出: 体积、利用率、切割数量、奇数行排列零件个数、偶数行排
列零件个数、奇数列排列零件个数、偶数列排列零件个数
AllResults = zeros(size(EllipsesParameters, 1) + size(CircleParameters, 1), 7);
count = 1;
% 正圆椭圆柱结果
disp('----------正圆椭圆柱结果---------------')
for ii = 1:size(EllipsesParameters, 1) disp('---------------------------------') ellipses.a = EllipsesParameters(ii,1)/2; ellipses.b = EllipsesParameters(ii, 2)/2; ellipses.h = EllipsesParameters(ii, 3)/2; ResultTemp = Ellipses(box, ellipses); AllResults(count, :) = ResultTemp; count = count + 1; pause(2)
end
% 正圆柱结果
disp('--------正圆柱结果--------------------')
for ii = 1:size(CircleParameters, 1) disp('---------------------------------') circle.r = CircleParameters(ii, 1)/2;circle.h = CircleParameters(ii, 2)/2; ResultTemp = Circle(box, circle); AllResults(count, :) = ResultTemp; count = count + 1; pause(2)
end
% 总利用率的计算
disp('-------------总的结果-----------------')
material_percentage = sum(AllResults(:, 1))/(box.x*box.y*box.z*6);
disp(['总原料利用率:',num2str(round(material_percentage*100,2)),'%']);
这篇关于2020年华数杯数学建模B题工业零件切割优化方案设计求解全过程文档及程序的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






