基于混合策略的鲸鱼优化算法-2023国赛数学建模A题第三问解题思路 - 定日镜场的优化设计（详细过程，小白读完就会）

鲸鱼优化算法（Whale Optimizaition Algorithm,WOA）是近年来新兴的一种群智能优化算法，该算法于 2016年由澳大利亚学者 Mirjalili等人[36]根据座头鲸的狩方式特点bubble-net觅食策略而提出。其最大特点就是螺旋线来模拟座头鲸的泡泡网攻击机制。该算法含有三种搜索机制，分别为包围猎物、泡泡网攻击模式（局部搜索行为）、座头鲸随机游动捕食（全局搜索行为）。因其算法结构相对简单且收敛性较好，其已被成功应用于很多领域的优化问题之中，如轨迹规划[37]、图像分割[38]、故障检测等[39]。

4.1鲸鱼优化算法原理

座头鲸由于其自身特点，捕食方式十分巧妙，它通过在水中吹出圆形气泡以制造水网包围猎物并将其困于气泡之中。在水下 15米左右，座头鲸会以螺旋形姿势向上游动，并吐出大量大小不一的气泡，使最后吐出的气泡与最初吐出的气泡同时到达水面，形成一种圆柱形或管形的气泡网，这些网会将猎物紧紧包围起来并逼向中心区域，这是座头鲸会以近乎直立姿态吞下网集中的猎物。座头鲸捕食行为如图 4.1所示。

 4.2算法数学模型

受座头鲸气泡网捕食行为的启发，Mirjalili等人将座头鲸捕食过程大致分为 3个阶段，从而形成鲸鱼算法中各部分寻优策略。在 WOA算法中包含三个阶段：搜寻猎物、包围猎物、气泡网攻击

4.2.1搜寻猎物阶段

鲸鱼在包围猎物时，会向着最优位置的鲸鱼或者种群中随机某鲸鱼的位置游动。对应优化问题时，个体鲸鱼位置即为问题的某可行解，而在算法每次迭代后，当前迭代次数中所搜寻到种群中的最优解即为目前最接近全局最优解的存在。在此阶段，鲸鱼个体会随机选择种群中其他鲸鱼的位置信息进行位置更新，而这种方式也能使算法具备一定的全局寻优能力。根据第 t次迭代的所得鲸鱼种群中的所有位置信息，当∣A∣>1时，种群中第 i个鲸鱼进行全局搜索[41]，数学表述为 ：

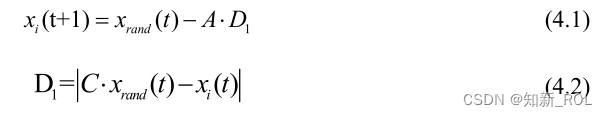
式中，xrand(t)表示第 t代鲸鱼群体中某一任意鲸鱼个体的位置；D1表示选中的任意鲸鱼个体与搜索个体之间距离的欧氏距离；t表示当前迭代次数；xi(t+1)表示第 t+1代中第i只鲸鱼个体的位置。A与 C是系数向量，计算公式如下：

式中， 1r与 2r为[0,1]区间上的随机数； a为算法收敛因子[42]。其表达式如下：

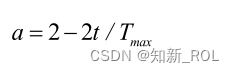
式中，Tmax为最大迭代次数。

4.2.2包围猎物阶段

当∣A∣≦1时，算法进入包围猎物阶段，此时个体会通过种群内最优鲸鱼的个体信息进行位置更新。由于最初搜索时猎物位置信息较模糊，WOA算法假设此时鲸鱼群中适应度值最优的解为猎物位或已逼近目标猎物位置，因此其他鲸鱼根据当前最优解的位置信息进行位置更新，通过逐步包围收缩，接近猎物并确定位置

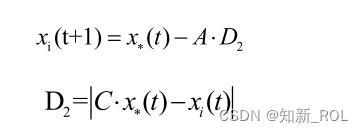
式中， x t表示第 t代中鲸鱼群体中最优鲸鱼个体的位置； D2表示最优鲸鱼个体与种群中第 i个个体的欧式距离。

4.2.3气泡网攻击阶段

座头鲸在气泡网攻击阶段会不断收缩减小猎物包围圈的同时会向上做螺旋运动进行捕食，根据其行为模式 WOA算法在该阶段设计了收缩包围机制和螺旋位置更新

（1）收缩包围机制
该机制主要通过公式 4.5中的 a来实现。a会从 2到 0随着迭代次数的增加线性递减[43]，A则是[a,a]范围内的随机数，且其波动范围随 a的减小而减小，这也保障了在算法迭代前期进行全局搜索的概率更大，而在中后期只会进行局部搜索。在收缩包围机制中，搜索到的个体其位置处于原始位置与最优个体位置之间的区域。二维问题收缩包围机制如图 4.2所示，表示了在二维问题解空间中当（X,Y）到（X*,Y*）的可能位置。

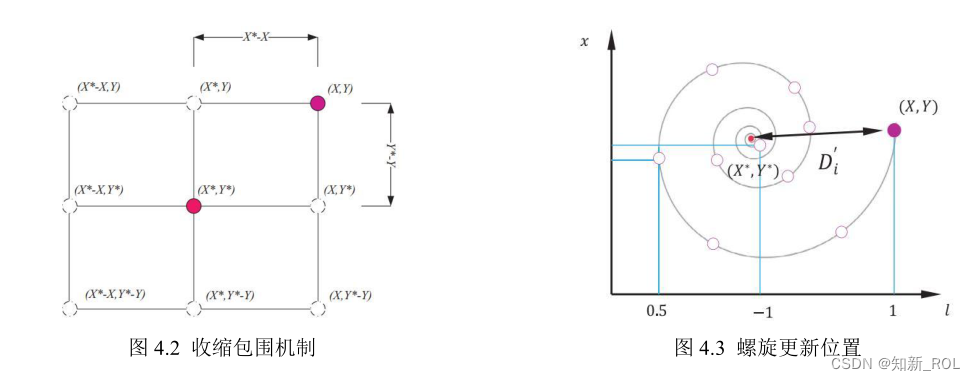
根据鲸鱼发起气泡网攻击时，吐气泡的同时进行螺旋式上升的行为特点，在鲸鱼和猎物之间建立螺旋方程，螺旋更新位置方式如图 4.3所示。数学模型表述如下：

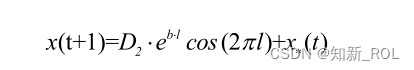
式中，b为螺旋方程的常量系数，取值为 1；D2表示最优鲸鱼个体与搜索个体之间的欧氏距离；l为[-1,1]区间内的随机数。

为了模拟鲸鱼同步进行包围收缩和气泡网攻击的狩猎行为，设计随机策略对位置更新方式进行选择。当随机概率 p≥0.5时，鲸鱼以气泡网螺旋式进行位置更新；当 p<0.5时，鲸鱼根据当前最优个体的位置信息进行位置更新。在不断逼近目标的迭代过程中，│A│持续减小，当│A│=0时，算法迭代结束，最后一次迭代所找到的最优个体位置信息即对应理论最优值的可行解，数学描述如下：

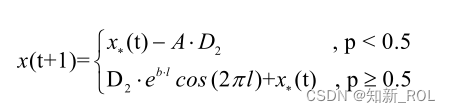
4.3基于混合策略的鲸鱼优化算法（MSWOA）

鲸鱼优化算法目前应用较为广泛，但其仍有一些不足之处，例如求解精度不足、收敛速度慢、迭代后期没有跳出局部最优的操作等。因此，针对上述问题，本文提出了基于混合策略的鲸鱼优化算法（Mixed Strategy Whale Optimizaition Algorithm,MSWOA）。首先，利用 Kent映射初始化种群以使得初始解在解空间得以均匀分布，增加在迭代初期即遇到优良解的可能性；然后构造动态双子群收敛因子代替原算法中的线性收敛因子，同时添加自适应惯性权重，以平衡全局搜索和局部搜索的能力；最后引入自适应精英变异策略提升算法跳出局部最优的能力。为验证改进算法的性能，选取一定数量的典型测试函数，在多个维度上与应用十分成熟的算法进行比较。

4.3.1基于 Kent混沌映射的种群初始化

（1）Logistic映射与Kent映射

在优化领域，混沌映射可以替代伪随机数生成器，生产 0到 1之间的混沌数。大量研究和实验表明，利用混沌序列对算法进行改进，往往能获得比伪随机数更好的效果[44]。而在元启发式算法领域，更是有很多学者通过引入混沌系统来对算法进行改进，使得算法中变量的分布可以具备更好的遍历性从而加快算法的收敛速度。其中引用最为普遍且效果较好的就是Logistic映射。Logistic混沌映射是混沌系统中一类十分经典且被广泛研究的动力系统[45]，同时现有的很多混沌优化算法均采用Logistic映射生成初始化种群。Logistic映射的系统方程:

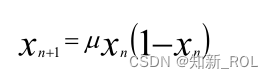
式中， u为控制参数，取值范围 0 -4。

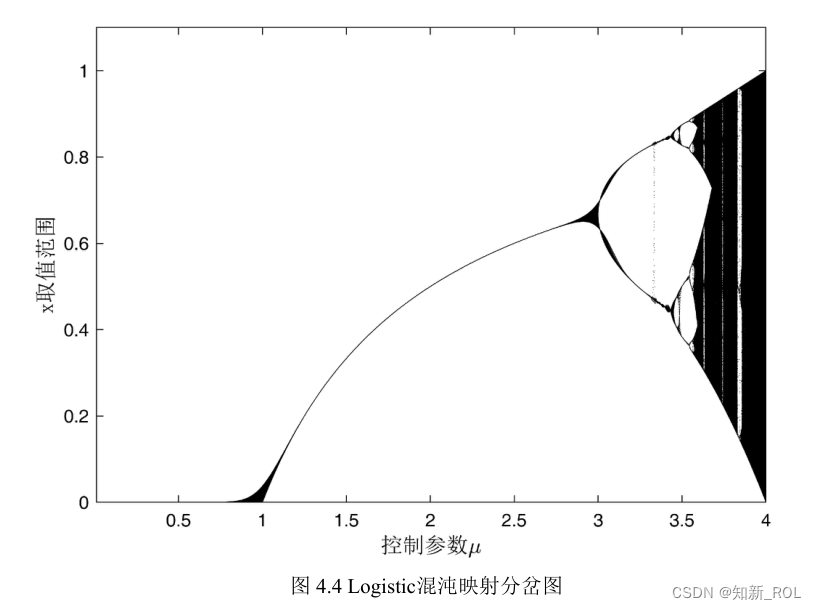
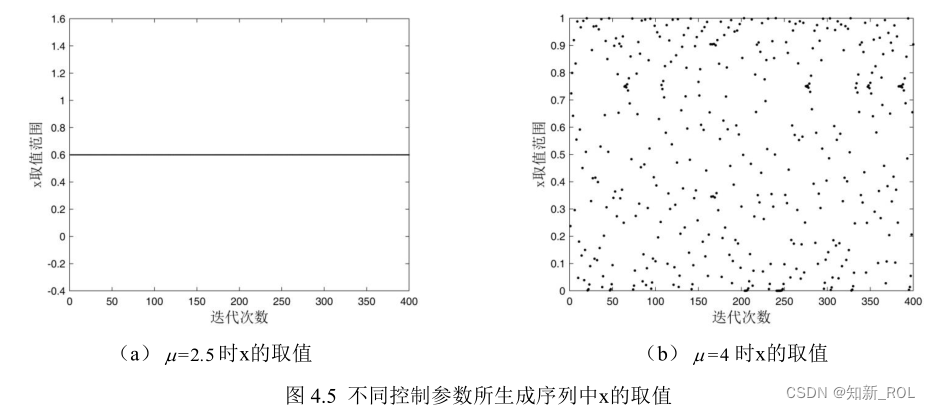
为清晰呈现μ的取值对Logistic映射的影响，分别得到μ取 2.5和 4时所生成对应序列
的具体情况，如图 4.5所示。

 在研究动力系统的分岔、混沌运动特性中，Lyapunov指数是衡量系统动力学特性的一个十分重要的定量指标，它表征了系统在相空间中相邻轨道间收敛或发散的平均比率。
该指数计算公式如下：

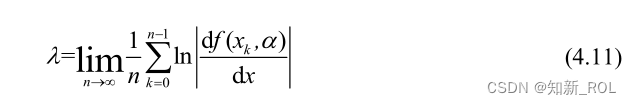
通过计算，在 Logistic映射中，当μ=4时，该映射的 Lyapunov指数最大，数值约为0.6931。Logsitic映射的 Lyapunov指数图如图 4.6所示。

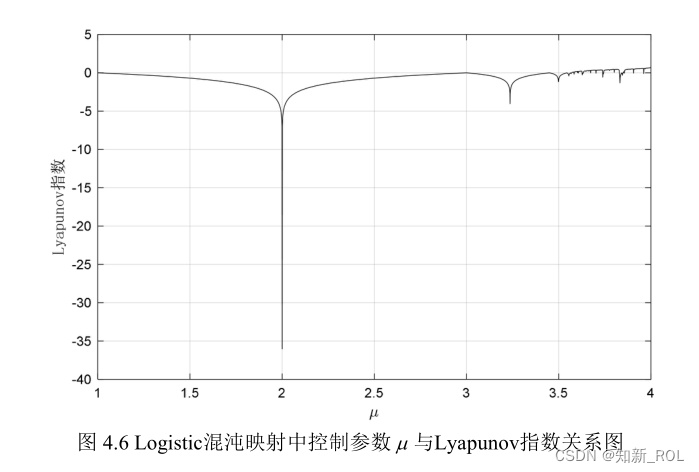
 在元启发式算法的种群初始化改进中，因希望通过混沌映射获取多样性更好的种群初始位置，所以也要着重考虑映射的遍历性，而遍历性又可通过映射所生成序列的概率密度来体现。Logistic映射的概率密度如图 4.7所示。

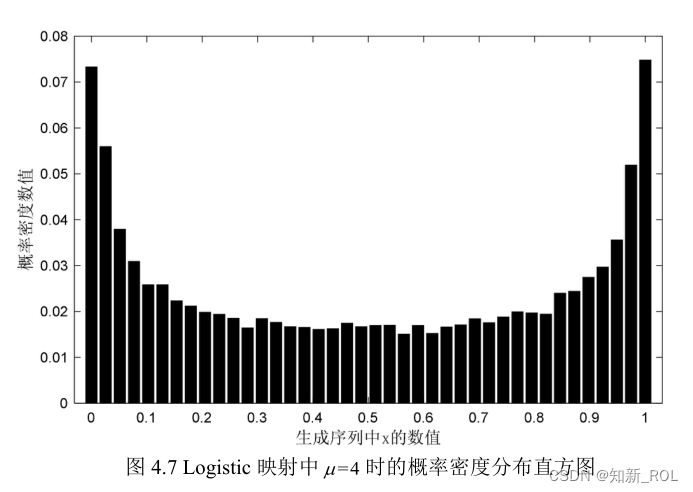
从图 4.7发现，Logistic映射概率密度分布呈现中间平缓，两侧边缘处概率密度骤然增大的特点，因此 Logistic映射的遍历均匀性较差。与Logistic映射相似，Kent映射同样具有拓扑共轭的性质，因此Kent映射也适用于在群智能算法中对种群初始化进行改进。

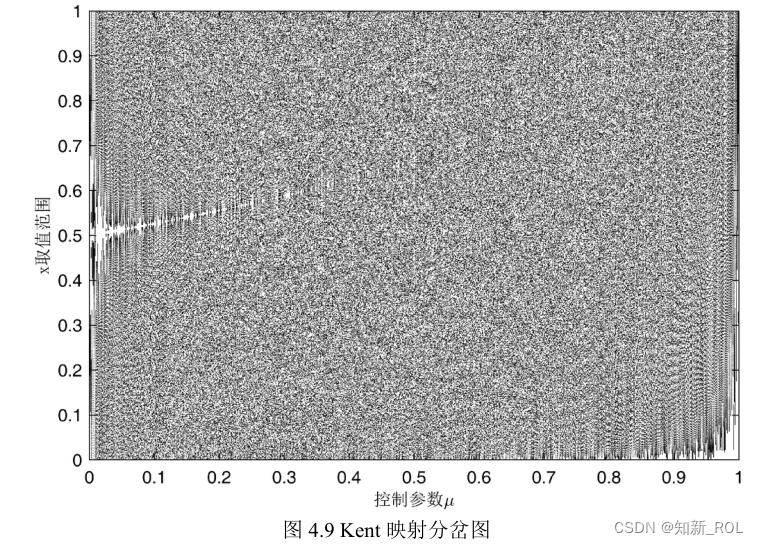
Kent映射的系统方程：

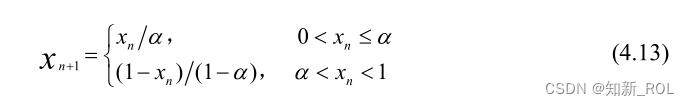
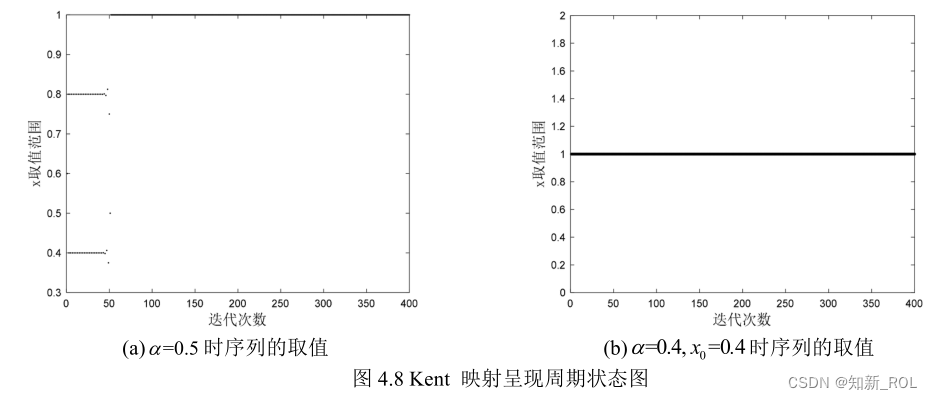
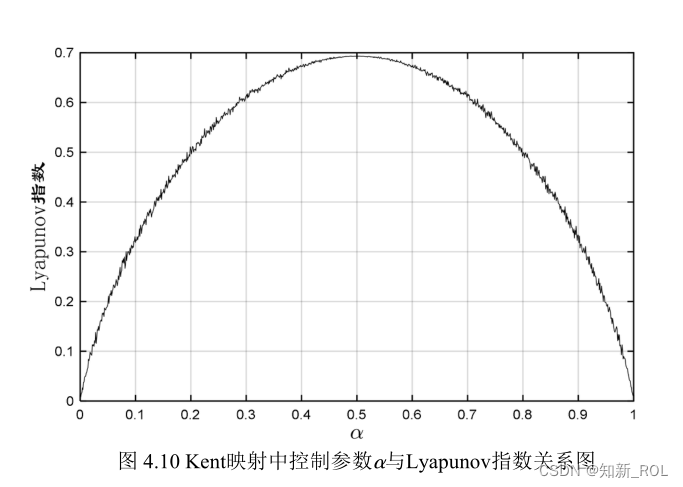
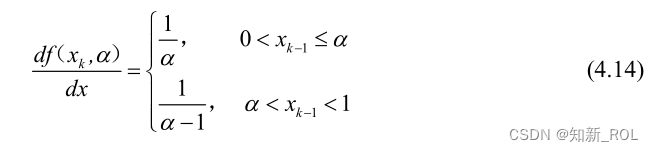通过计算，Kent映射在控制参数=0.489时，Lyapunov指数最大，数值值为 0.6934。Kent映射的 Lyapunov指数图如图 4.10所示。

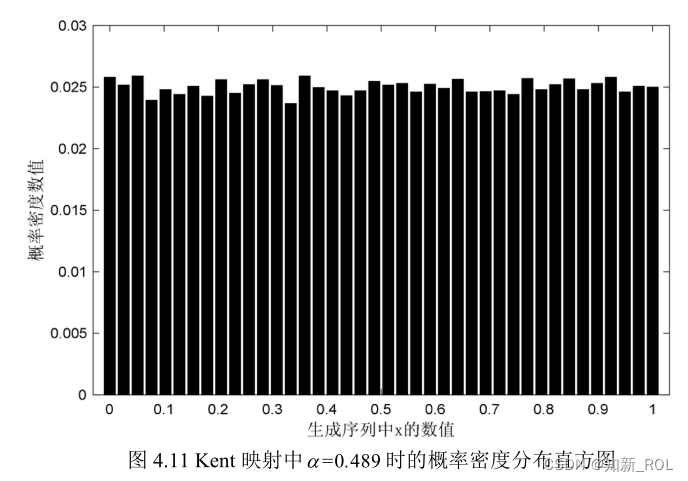
选取Kent映射中混沌性最好时对应的控制参数，即最大Lyapunov指数所对应的控制参数，迭代生成混沌序列并得到概率密度图，如图 4.11所示。

 （2）种群初始化改进

4.3.2动态双子群收敛因子

 鲸鱼优化算法中，个体更新位置信息时是进行全局搜索还是局部开发主要受参数 A的影响，而 A主要由 a决定，a会随着迭代次数的增加逐渐递减。这样的变化大大降低了算法的开发能力以及种群的多样性。在算法迭代过程中，全局最优解通常在局部最优解的附近，故依靠种群中适应度值较高的个体，算法可更好地进行局部搜索，而根据适应度值较差的个体，算法可以更好地进行全局搜索，因此种群的进化程度在很大程度上受落后个体的影响。结合动态双子群策略[49]，本文提出了一种适用于鲸鱼优化算法的动态双子群收敛因子。定义种群中当前个体与最优个体和最差个体的欧氏距离分别为 Dbest和 Dworst，以 Dbest≦（Dworst/4）为标准，将该个体划分为以当代最优鲸鱼个体位置为几何中心的较优子群；否则将该个体划分为以当代最差鲸鱼个体位置为中心的较差子群。根据两个子群的特点，采取不同的非线性收敛因子，以平衡局部搜索能力和全局搜索能力。较优子群的收敛因子 a1与较差子群的收敛因子 a2如下所示：

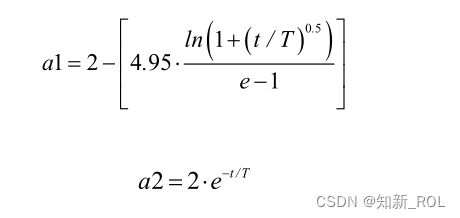
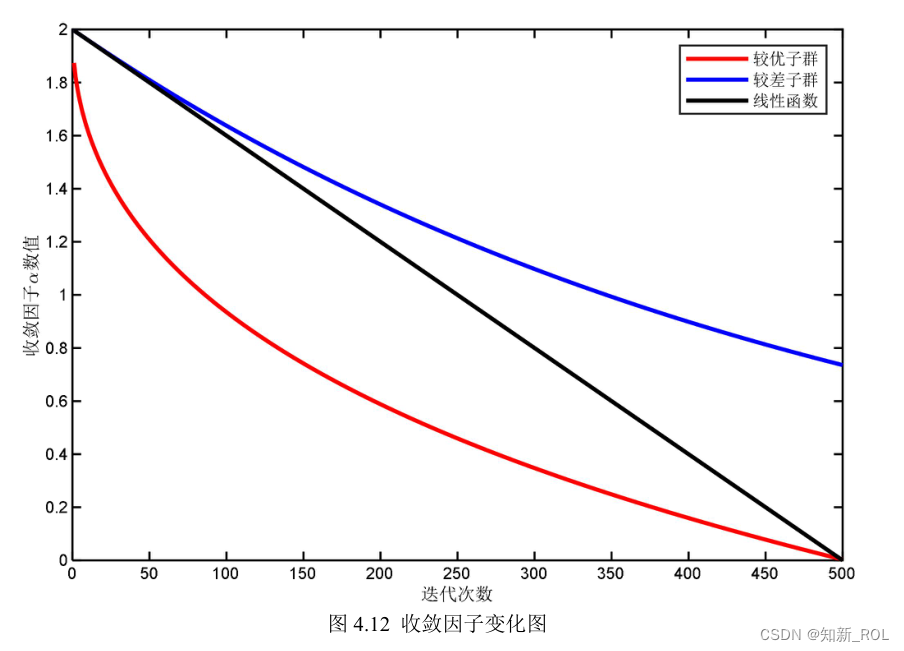
对于较优子群，因其距离当前迭代中所得的最优个体位置较近，故应尽快进入收缩包围机制，快速向当前最优个体靠近，所 a1在迭代初期应快速减小，在后期为避免算法陷入局部最优，应使得 a1缓慢下降；而对于较差子群，因其距离当前迭代中所得的最优个体位置较远，为使它们尽快找到较优值，需保证其在更大范围内进行全局搜索，故 a2需要缓慢减小，而在迭代后期，使得 a2仍保持较大值可以保证在设定迭代次数内如果寻优结果依旧未收敛时，种群在后期能够以较大的步长搜索最优解。 原算法中收敛因子及改进后所添加的动态双子群收敛因子随迭代次数的变化情况，
如图 4.12所示。

4.3.3自适应精英非均匀变异（AENM）

鲸鱼优化算法中种群在进化时，每个粒子的搜索潜力各不相同，为充分发挥优势粒子的潜力、避免算法陷入局部最优、进一步提高算法效率[50]，本文在结合精英策略和非均匀变异策略的基础上，同时引入一种新的自适应算子动态地调整变异分量，给予种群中适应度值较优及较差的部分粒子更多的进化机会，若通过变异操作得到了新的优势点，则将其替代种群中被选择的原个体。本文将这种融入了精英策略和自适应动态算子的非均匀变异方法 [51]称为“自适应精英非均匀变异（AENM,Adaptive elite non-uniformmutation strategy）”

在精英策略中，精英粒子入选比例的确定对问题的求解十分关键。一方面，比例过大，种群多样性随着进化过程的深入而大幅度降低；另一方面，一些理论分析表明，在末端收敛前，种群搜寻的全局最优位置总是在先前已知的几个候选解中来回振荡[50]。因此，本算法中仅将种群中的 gbest作为精英粒子，以其位置信息为基础，通过自适应操作计算出非均匀变异所需要的自适应变异算子。

在 AENM变异操作中，首先以自适应方式生成变异种子 xm与变异常量 C，二者结合产生自适应变异算子，再通过自适应变异算子与非均匀变异分量得出相对应的真实变异量。其中，xm由所选择的个体到精英粒子的欧式距离 r以及迭代次数 t的综合决定，根据公式 1.17、1.18可求出 pbest到 gbest在各维上的距离，距离越大，表示群体间相似性越小，距离越小，则表示群体间相似性越大；再依据公式 1.19即适应度标准差 st_d的不同取值，自适应地获取相对应的变异常量 C ，并依据公式 1.20生成自适应变异算子 F(xm)；依据公式 1.21、1.22得出具体的真实变异量从而得到变异位 gbest*，若变异后的 f(gbest)优于 f(gbest*)，则种群中的 gbest被 gbest*取代。同时，考虑到要加快算法的寻优进程，故分别选择种群中 20%的较优粒子和 20%的较差粒子进行变异操作。在 AENM变异中，各维间距离的计算公式为：

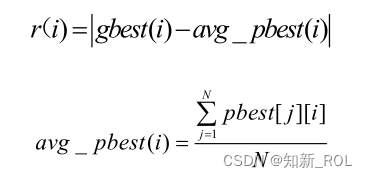
式中，r(i)表示种群中选择进行变异操作的 N个个体即 N个 pbest在各维上的平均值avg_pbest(i)到 gbest(i)的距离；gbest(i)表示迭代中最优粒子的第 i维的位置信息；pbest[j][i]是种群中第 j个粒子的第 i维的位置信息。在 AENM变异中，变异种子的计算公式为：

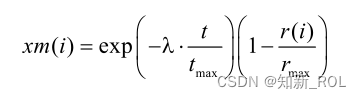
 式中，i=1,2,3….D； 为常数，取值为 10； rmax为 rmax各维间最大距离。在 AENM变异中，自适应变异算子的计算公式为：

在 AENM变异中，自适应变异常量的计算公式为：

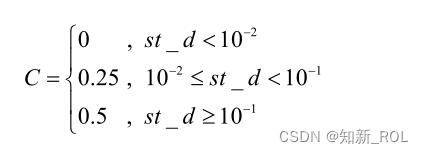
 4.3.4自适应惯性权重

Shi等人首次将惯性权重因子w引入 PSO算法，并取得了较为理想的效果，随后的众多研究也证明了w对平衡算法全局和局部搜索能力的重要性

引入惯性权重时因考虑到，在 WOA算法初期，个体适应度值普遍低且位置距离最优值较远，此时种群更适合在整个解空间进行探索即需要较高的惯性权重；而在后期，种群向适应度值高的个体集中，此时若采用低惯性权重，则种群的开发能力有限，容易陷入局部最优。因此，设计自适应动态惯性权重因子的基本思想是应满足在算法进化前期主要对解空间进行全面探索以期尽快到达较优区域；在迭代后期主要对较优区域进行开发以期找到最优解自适应惯性权重计算公式，如下所示：